目录
7-1 列出连通集
题目
输入格式:
输出格式:
输入样例:
输出样例:
AC代码
7-2 六度空间
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码
7-3 地下迷宫探索
题目
输入格式:
输出格式:
输入样例1:
输出样例1:
输入样例2:
输出样例2:
思路
AC代码
7-4 社交网络图中结点的“重要性”计算
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码
7-5 List Components
题目
Input Specification:
Output Specification:
Sample Input:
Sample Output:
思路
AC代码
7-6 排座位
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码
7-7 红色警报
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码
7-8 家庭房产
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码
7-9 肿瘤诊断
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码(BFS)
没有AC的代码(调了很久,还是2/30)。
7-10 图着色问题
题目
输入格式:
输出格式:
输入样例:
输出样例:
思路
AC代码
7-11 拯救007
输入格式:
输出格式:
输入样例 1:
输出样例 1:
输入样例 2:
输出样例 2:
思路
AC代码
7-1 列出连通集
题目
分数 25
作者 陈越
单位 浙江大学
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v1 v2 ... vk }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
AC代码
#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
int mat[11][11];
bool visited[12];
vector<int> v;
void dfs(int cur,int n)
{
visited[cur]=true;
v.push_back(cur);
for(int i=0;i<n;i++)
{
if(visited[i]==true||i==cur)
continue;
if(mat[cur][i]==1)
dfs(i,n);
}
}
void bfs(int cur,int n)
{
queue<int> Q;
Q.push(cur);
visited[cur]=true;
v.push_back(cur);//v存放cur所在的连通集
while(!Q.empty())
{
int k=Q.size();
for(int i=0;i<k;i++)
{
//取队头元素的所有直接联通点
for(int j=0;j<n;j++)
{
if(visited[j]==true||Q.front()==j)
continue;
if(mat[Q.front()][j]==1)
{
Q.push(j);
visited[j]=true;
v.push_back(j);
}
}
Q.pop();
}
}
}
int main()
{
int n,e;
cin>>n>>e;
for(int i=0;i<e;i++)
{
int a,b;
cin>>a>>b;
mat[a][b]=mat[b][a]=1;
}
memset(visited,false,sizeof(visited)/sizeof(bool));
//dfs
for(int i=0;i<n;i++)
{
v.resize(0);
if(visited[i]==false)
dfs(i,n);
for(int j=0;j<v.size();j++)
{
if(j==0)
cout<<"{ ";
cout<<v[j]<<" ";
if(j==v.size()-1)
cout<<"}\n";
}
}
//bfs
memset(visited,false,sizeof(visited)/sizeof(bool));
for(int i=0;i<n;i++)
{
v.resize(0);
if(visited[i]==false)
bfs(i,n);
for(int j=0;j<v.size();j++)
{
if(j==0)
cout<<"{ ";
cout<<v[j]<<" ";
if(j==v.size()-1)
cout<<"}\n";
}
}
}7-2 六度空间
题目
分数 30
作者 DS课程组
单位 浙江大学
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。

图1 六度空间示意图
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤103,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%
代码长度限制
16 KB
时间限制
2500 ms
内存限制
64 MB
思路
广度优先搜索,通过几层的搜索能找到另一人就是两个人之间的间隔。
AC代码
这题是刚学数据结构时写的,里面有一些复杂的结构。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define MVNum 1000
#define Maxint 32767
using namespace std;
bool visited[MVNum];
typedef int VerTexType;
typedef int ArcType;
//邻接表
typedef struct ArcNode {//边
int adjvex; //边所指向顶点的位置
struct ArcNode* nextarc; //下一个边
}ArcNode;
typedef struct VNode {//顶点
VerTexType date;
ArcNode* firstarc;
}VNode, AdjList[MVNum];
typedef struct { //邻接表
AdjList vertices;
int vexnum, arcnum;
}ALGraph;
void CreateUDG(ALGraph& G)
{//创建无向图的邻接表
cin >> G.vexnum >> G.arcnum;
//顶点赋初值
for (int i = 0; i < G.vexnum; i++)
{
G.vertices[i].date = i + 1;
G.vertices[i].firstarc = NULL;
}
for (int k = 0; k < G.arcnum; k++)
{
int i, j;
cin >> i >> j;
i--;
j--;
ArcNode* p1, * p2;
//i邻接一条边j
p1 = new ArcNode;
p1->adjvex = j;
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1;
//j邻接一条边i
p2 = new ArcNode;
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p2;
}
}
double BFS_AL(ALGraph& G, int v)
{//从下标为V的点开始广度优先搜索,对邻接表
// cout << "从下标" << v << "开始查找:";
int friends = 0;
int step = 0;//节点之间的距离
memset(visited, false, sizeof(bool) * G.vexnum);
queue<VNode>Q; //队列的元素是邻接表的点,不是邻接表边
Q.push(G.vertices[v]);
visited[v] = true;
while (!Q.empty() && step < 6)
{
step++;
// cout << "\n第" << step << "步访问的下标:";
//取队里的所有点,并将这些元素的未标记的邻接点放进队列
int n = Q.size();
for (int i = 0; i < n; i++)
{
VNode p = Q.front();
Q.pop();
//找出队元素所有未被访问的邻接点 (即找某个人的所有朋友)
ArcNode* q = p.firstarc;
while (q != NULL)
{
if (visited[q->adjvex] == false)
{
visited[q->adjvex] = true;
Q.push(G.vertices[q->adjvex]);
}
q = q->nextarc;
}
}
}//while
//计算比例 ,六步之内找到的朋友(包括自己)/总人数
for (int i = 0; i < G.vexnum; i++)
if (visited[i] == true) friends++;
// cout << "vexnum=" << G.vexnum << " " << "friends=" << friends << " ";
return 1.0 * friends / G.vexnum;
}
int main()
{
ALGraph G;
CreateUDG(G);
for (int i = 0; i < G.vexnum; i++)
{
double a = 100 * BFS_AL(G, i);
printf("%d: %.2lf%%\n", i + 1, a);
}
return 0;
}7-3 地下迷宫探索
题目
分数 30
作者 DS课程组
单位 浙江大学
地道战是在抗日战争时期,在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事,如下图所示。

我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?

输入格式:
输入第一行给出三个正整数,分别表示地下迷宫的节点数N(1<N≤1000,表示通道所有交叉点和端点)、边数M(≤3000,表示通道数)和探索起始节点编号S(节点从1到N编号)。随后的M行对应M条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出格式:
若可以点亮所有节点的灯,则输出从S开始并以S结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
输入样例1:
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
输出样例1:
1 2 3 4 5 6 5 4 3 2 1
输入样例2:
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
输出样例2:
6 4 5 4 6 0
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
思路
深度优先搜索。但是这题并不是说每个节点只遍历一次,而是说在遍历完所有的节点的过程中,访问某个节点和访问完这个节点回溯时都要打印一次。
AC代码
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int SIZE = 1005;
int N, M, S;
int cnt = 0; //记录输出的数量,防止多输出空格
vector<vector<int>> arc;
vector<int> path;
int visited[SIZE];
void inif()
{
arc.resize(N + 1);
for (int i = 0; i < M; i++)
{
int arc1, arc2;
cin >> arc1 >> arc2;
arc[arc1].push_back(arc2);
arc[arc2].push_back(arc1);
}
//排序,优先访问序列小的节点
for (int i = 1; i <= N; i++)
{
sort(arc[i].begin(), arc[i].end());
}
}
void dfs(int i)
{
visited[i] = 1;
cnt++;
//点灯时输出一次
if (cnt == 1) cout << i;
else cout << " " << i;
for (int j = 0; j < arc[i].size(); j++)
{
if (visited[arc[i][j]] == 0)
{
dfs(arc[i][j]);
//点完相邻的灯后输出一次
cout << " " << i;
}
}
}
int main()
{
cin >> N >> M >> S;
inif();
dfs(S);
if(cnt!=N) cout<<" 0";
}7-4 社交网络图中结点的“重要性”计算
题目
分数 30
作者 DS课程组
单位 浙江大学
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi的“紧密度中心性”Cc(vi)数学上定义为vi到其余所有结点vj (j=i) 的最短距离d(vi,vj)的平均值的倒数:

对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤104)是图中结点个数,顺便假设结点从1到N编号;M(≤105)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35
代码长度限制
16 KB
时间限制
20000 ms
内存限制
64 MB
思路
用广度优先搜索计算某个点到其他点的距离。其间用一个数记录联通点的数量,若联通点的数量不等于N,就全输出0。
AC代码
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int MAXSIZE=10005;
int N,M,K;
vector<vector<int>> f; //用于记忆化
vector<vector<int>> arcs; //邻接表
int visited[MAXSIZE];
bool flag=true; //标志是否连通
int cnt=0; //联通点的数量
void inif()
{
cin>>N>>M;
arcs.resize(N+1);
for(int i=0;i<M;i++)
{
int arc1,arc2;
cin>>arc1>>arc2;
arcs[arc1].push_back(arc2);
arcs[arc2].push_back(arc1);
}
}
void MEMSET(){for(int i=1;i<=N;i++) visited[i]=0;}
long long bfs(int x)
{
if(!flag) return -1;
MEMSET();
long long sum=0;
int length=0;//点x到某个点的长度
queue<int> q;
q.push(x);
visited[x]=1;
cnt=1;
while(!q.empty()){
int size=q.size();
++length;
for(int i=0;i<size;i++){
int cur=q.front();
q.pop();
for(auto arc:arcs[cur]){
if(visited[arc]==0){
q.push(arc);
++cnt;
visited[arc]=1;
sum+=length;
}
}
}
}
if(cnt!=N){
flag=false;
return -1;
}
return sum;
}
void slove()
{
cin>>K;
for(int i=0;i<K;i++){
if(i!=0) cout<<endl;
int x;
cin>>x;
if(!flag){
cout<<"Cc("<<x<<")=0.00";
continue;
}
double aver=1.0*(N-1)/bfs(x);
if(!flag){
cout<<"Cc("<<x<<")=0.00";
continue;
}
printf("Cc(%d)=%.2lf",x,aver);
}
}
int main()
{
inif();
slove();
}7-5 List Components
题目
分数 25
作者 陈越
单位 浙江大学
For a given undirected graph with N vertices and E edges, please list all the connected components by both DFS (Depth First Search) and BFS (Breadth First Search). Assume that all the vertices are numbered from 0 to N-1. While searching, assume that we always start from the vertex with the smallest index, and visit its adjacent vertices in ascending order of their indices.
Input Specification:
Each input file contains one test case. For each case, the first line gives two integers N (0<N≤10) and E, which are the number of vertices and the number of edges, respectively. Then E lines follow, each described an edge by giving the two ends. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print in each line a connected component in the format { v1 v2 ... vk }. First print the result obtained by DFS, then by BFS.
Sample Input:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
Sample Output:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
思路
这是一个英文题,稍微阅读一下然后和7-1的输入输出对比一下会发现,这题就是7-1的英文版。
AC代码
#include<iostream>
#include<queue>
using namespace std;
int f[15][15];
int visited[15];
int N, E;
vector<int> g;
int flag = false;
void dfs(int i)
{
for (int j = 0; j < N; j++) {
if (f[i][j] == 1 && visited[j] == 0) {
g.push_back(j);
visited[j] = 1;
dfs(j);
}
}
}
void bfs(int i)
{
queue<int> q;
q.push(i);
g.push_back(i);
visited[i] = 1;
while (!q.empty()) {
int cur = q.front();
q.pop();
for (int j = 0; j < N; j++) {
if (f[cur][j] == 1 && visited[j] == 0) {
visited[j] = 1;
g.push_back(j);
q.push(j);
}
}
}
}
int main()
{
cin >> N >> E;
for (int i = 0; i < E; i++) {
int x, y;
cin >> x >> y;
f[x][y] = f[y][x] = 1;
}
for (int i = 0; i < N; i++) {
if (visited[i] == 0) {
visited[i] = 1;
g.resize(0);
g.push_back(i);
dfs(i);
if (flag == true) cout << endl;
flag = true;
cout << "{ ";
for (int j = 0; j < g.size(); j++) {
cout << g[j] << " ";
}
cout << "}";
}
}
for (int i = 0; i < N; i++) visited[i] = 0;
for (int i = 0; i < N; i++) {
if (visited[i] == 0) {
g.resize(0);
bfs(i);
if (flag == true) cout << endl;
flag = true;
cout << "{ ";
for (int j = 0; j < g.size(); j++) {
cout << g[j] << " ";
}
cout << "}";
}
}
}7-6 排座位
题目
分数 25
作者 陈越
单位 浙江大学
布置宴席最微妙的事情,就是给前来参宴的各位宾客安排座位。无论如何,总不能把两个死对头排到同一张宴会桌旁!这个艰巨任务现在就交给你,对任何一对客人,请编写程序告诉主人他们是否能被安排同席。
输入格式:
输入第一行给出3个正整数:N(≤100),即前来参宴的宾客总人数,则这些人从1到N编号;M为已知两两宾客之间的关系数;K为查询的条数。随后M行,每行给出一对宾客之间的关系,格式为:宾客1 宾客2 关系,其中关系为1表示是朋友,-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行,每行给出一对需要查询的宾客编号。
这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友,朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。
输出格式:
对每个查询输出一行结果:如果两位宾客之间是朋友,且没有敌对关系,则输出No problem;如果他们之间并不是朋友,但也不敌对,则输出OK;如果他们之间有敌对,然而也有共同的朋友,则输出OK but...;如果他们之间只有敌对关系,则输出No way。
输入样例:
7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2
输出样例:
No problem
OK
OK but...
No way
代码长度限制
16 KB
时间限制
200 ms
内存限制
64 MB
思路
并查集判断两个人是否是朋友(的朋友的朋友的朋友……)。
AC代码
#include<iostream>
using namespace std;
const int MAXSIZE = 105;
int N, M, K;
int relation[MAXSIZE][MAXSIZE];
int fa[MAXSIZE * MAXSIZE];
int find(int x)
{
int r = x;
while (fa[r] != r)
{
fa[r] = fa[fa[r]];
r = fa[r];
}
return r;
}
void merge(int x, int y)
{
int fx = find(x);
int fy = find(y);
if (fx > fy) {
fa[fy] = fx;
}
else {
fa[fx] = fy;
}
}
int node(int i, int j) { return N * (i - 1) + j; }
void inif()
{
cin >> N >> M >> K;
for (int i = 1; i <= N; i++) {
fa[i] = i;
for (int j = 1; j <= N; j++) {
relation[i][j] = 0;
}
}
for (int i = 0; i < M; i++)
{
int x, y, c;
cin >> x >> y >> c;
relation[x][y] = relation[y][x] = c;
if (c == 1) merge(x, y);
}
}
void slove()
{
for (int i = 0; i < K; i++)
{
if (i != 0) cout << endl;
int x, y;
cin >> x >> y;
bool flag = (find(x) == find(y));
if (flag && relation[x][y] != -1) cout << "No problem";
else if (!flag && relation[x][y] != -1) cout << "OK";
else if (flag && relation[x][y] == -1) cout << "OK but...";
else cout << "No way";
}
}
int main()
{
inif();
slove();
}7-7 红色警报
题目
分数 25
作者 陈越
单位 浙江大学
战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序,当失去一个城市导致国家被分裂为多个无法连通的区域时,就发出红色警报。注意:若该国本来就不完全连通,是分裂的k个区域,而失去一个城市并不改变其他城市之间的连通性,则不要发出警报。
输入格式:
输入在第一行给出两个整数N(0 < N ≤ 500)和M(≤ 5000),分别为城市个数(于是默认城市从0到N-1编号)和连接两城市的通路条数。随后M行,每行给出一条通路所连接的两个城市的编号,其间以1个空格分隔。在城市信息之后给出被攻占的信息,即一个正整数K和随后的K个被攻占的城市的编号。
注意:输入保证给出的被攻占的城市编号都是合法的且无重复,但并不保证给出的通路没有重复。
输出格式:
对每个被攻占的城市,如果它会改变整个国家的连通性,则输出Red Alert: City k is lost!,其中k是该城市的编号;否则只输出City k is lost.即可。如果该国失去了最后一个城市,则增加一行输出Game Over.。
输入样例:
5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3
输出样例:
City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
思路
构建好图后先记录一次连通集个数。随后每删除一个点就更新一次连通集个数。若连通集个数没变或只是减了一个,则说明没有改变整个国家的连通性。
AC代码
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int MAXSIZE = 505;
int N, M, K;
vector<vector<int>> g;
int book[MAXSIZE];
int lost[MAXSIZE];//==1表示已经失去
int unionCount = 0;
int func()
{
int sum = 0;
for (int i = 0; i < N; i++) book[i] = 0;
for (int i = 0; i < N; i++) {
if (book[i] == 1 || lost[i] == 1) continue;
sum++;
queue<int> q;
q.push(i);
while (!q.empty()) {
int cur = q.front();
q.pop();
for (int j = 0; j < g[cur].size(); j++) {
int node = g[cur][j];
if (lost[node] == 1 || book[node] == 1) continue;
q.push(node);
book[node] = 1;
}
}
}
return sum;
}
void slove()
{
cin >> K;
int aim;
for (int i = 0; i < K; i++) {
cin >> aim;
if (i != 0) cout << endl;
lost[aim] = 1;
int cnt = func();
if (cnt == unionCount || cnt == unionCount - 1) {
cout << "City " << aim << " is lost.";
}
else {
cout << "Red Alert: City " << aim << " is lost!";
}
unionCount = cnt;//更新
if (i == N - 1) {
cout << "\nGame Over.";
}
}
}
int main()
{
cin >> N >> M;
g.resize(N);
for (int i = 0; i < M; i++) {
int x, y;
cin >> x >> y;
g[x].push_back(y);
g[y].push_back(x);
}
unionCount = func();
slove();
//cout << unionCount;
}7-8 家庭房产
题目
分数 25
作者 陈越
单位 浙江大学
给定每个人的家庭成员和其自己名下的房产,请你统计出每个家庭的人口数、人均房产面积及房产套数。
输入格式:
输入第一行给出一个正整数N(≤1000),随后N行,每行按下列格式给出一个人的房产:
编号 父 母 k 孩子1 ... 孩子k 房产套数 总面积
其中编号是每个人独有的一个4位数的编号;父和母分别是该编号对应的这个人的父母的编号(如果已经过世,则显示-1);k(0≤k≤5)是该人的子女的个数;孩子i是其子女的编号。
输出格式:
首先在第一行输出家庭个数(所有有亲属关系的人都属于同一个家庭)。随后按下列格式输出每个家庭的信息:
家庭成员的最小编号 家庭人口数 人均房产套数 人均房产面积
其中人均值要求保留小数点后3位。家庭信息首先按人均面积降序输出,若有并列,则按成员编号的升序输出。
输入样例:
10
6666 5551 5552 1 7777 1 100
1234 5678 9012 1 0002 2 300
8888 -1 -1 0 1 1000
2468 0001 0004 1 2222 1 500
7777 6666 -1 0 2 300
3721 -1 -1 1 2333 2 150
9012 -1 -1 3 1236 1235 1234 1 100
1235 5678 9012 0 1 50
2222 1236 2468 2 6661 6662 1 300
2333 -1 3721 3 6661 6662 6663 1 100
输出样例:
3
8888 1 1.000 1000.000
0001 15 0.600 100.000
5551 4 0.750 100.000
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
思路
这题要是一开始就告诉你出现过的人有几个并且所有人的编号都为1-N,那么这题就不难。难点就是所有人的编号是离散的,就要一些特殊处理。
我们用并查集来判断家庭的个数,每次合并两个人的时候,将编号大的指向编号小的。这样统计面积的时候就只需要将每个点的面积属性加到father数组的根当中即可。最后将家庭按照面积降序、最小编号升序的方式排序,然后输出。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int MAXSIZE=1e5+5;
int N;
int family=0;
int fa[MAXSIZE];
bool visited[MAXSIZE];
struct new_person{
int id,fid,mid,num,area,k;
int child[6];
} g[1005];
struct _ans{
int minid=0,people=0;
double num=0,area=0;
bool have=false;
} ans[MAXSIZE];
bool cmp(_ans a,_ans b)
{
if(a.area==b.area)
return a.minid<b.minid;
return a.area>b.area;
}
int find(int x)
{
int r=x;
while(fa[r]!=r) r=fa[r];
return r;
}
void merge(int x,int y)
{
int fx=find(x);
int fy=find(y);
if(fx<fy) fa[fy]=fx;
else if(fx>fy) fa[fx]=fy;
}
int main()
{
cin>>N;
for(int i=0;i<MAXSIZE;i++) fa[i]=i;
//处理输入数据
for(int i=0;i<N;i++){
cin>>g[i].id>>g[i].fid>>g[i].mid>>g[i].k;
visited[g[i].id]=true;
if(g[i].fid!=-1){
visited[g[i].fid]=true;
merge(g[i].id,g[i].fid);
}
if(g[i].mid!=-1){
visited[g[i].mid]=true;
merge(g[i].id,g[i].mid);
}
for(int j=0;j<g[i].k;j++){
cin>>g[i].child[j];
visited[g[i].child[j]]=true;
merge(g[i].id,g[i].child[j]);
}
cin>>g[i].num>>g[i].area;
}
//统计房产和每个家庭最小id
for(int i=0;i<N;i++){
int j=find(g[i].id);
ans[j].minid=j;
ans[j].num+=g[i].num; //房产个数
ans[j].area+=g[i].area; //房产面积
ans[j].have=true;
}
//统计每个家庭人数和家庭个数
for(int i=0;i<10000;i++){
if(visited[i]) ans[find(i)].people++;
if(ans[i].have) family++;
}
//将房产个数和房产面积转换为平均值
for(int i=0;i<10000;i++){
if(ans[i].have){
ans[i].num=(double)(1.0*ans[i].num/ans[i].people);
ans[i].area=(double)(1.0*ans[i].area/ans[i].people);
}
}
//排序并输出
sort(ans,ans+10000,cmp);
cout<<family;
for(int i=0;i<family;i++){
printf("\n%04d %d %.3lf %.3lf",ans[i].minid,ans[i].people,ans[i].num,ans[i].area);
}
}7-9 肿瘤诊断
题目
分数 30
作者 陈越
单位 浙江大学
在诊断肿瘤疾病时,计算肿瘤体积是很重要的一环。给定病灶扫描切片中标注出的疑似肿瘤区域,请你计算肿瘤的体积。
输入格式:
输入第一行给出4个正整数:M、N、L、T,其中M和N是每张切片的尺寸(即每张切片是一个M×N的像素矩阵。最大分辨率是1286×128);L(≤60)是切片的张数;T是一个整数阈值(若疑似肿瘤的连通体体积小于T,则该小块忽略不计)。
最后给出L张切片。每张用一个由0和1组成的M×N的矩阵表示,其中1表示疑似肿瘤的像素,0表示正常像素。由于切片厚度可以认为是一个常数,于是我们只要数连通体中1的个数就可以得到体积了。麻烦的是,可能存在多个肿瘤,这时我们只统计那些体积不小于T的。两个像素被认为是“连通的”,如果它们有一个共同的切面,如下图所示,所有6个红色的像素都与蓝色的像素连通。

输出格式:
在一行中输出肿瘤的总体积。
输入样例:
3 4 5 2
1 1 1 1
1 1 1 1
1 1 1 1
0 0 1 1
0 0 1 1
0 0 1 1
1 0 1 1
0 1 0 0
0 0 0 0
1 0 1 1
0 0 0 0
0 0 0 0
0 0 0 1
0 0 0 1
1 0 0 0
输出样例:
26
代码长度限制
16 KB
时间限制
1000 ms
内存限制
64 MB
思路
刚开始看不懂题目什么意思,后面发现,就是一个图结构,要我们判断所有体积大于T的连通块。
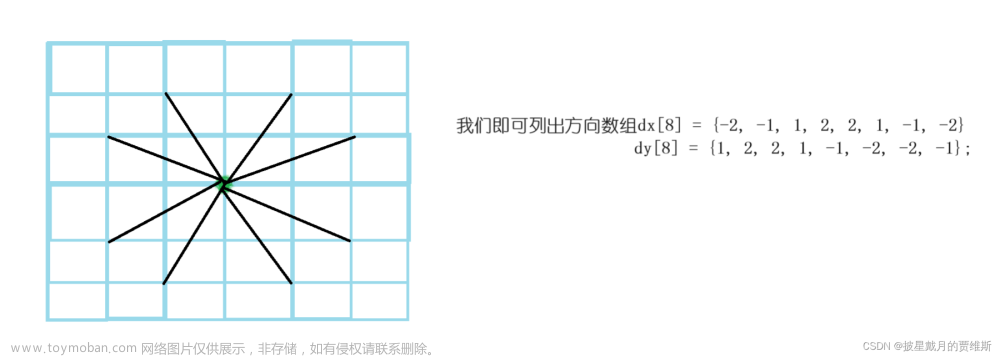
但是以往的邻接矩阵都是二维的,有四个方向。这次是三维的,有六个方向。
AC代码(BFS)
#include<iostream>
#include<queue>
using namespace std;
int M, N, L, T;
struct Node {
int x, y, z;
};
int dx[6] = { 1,-1,0,0,0,0 };
int dy[6] = { 0,0,1,-1,0,0 };
int dz[6] = { 0,0,0,0,1,-1 };
int f[1300][130][70];
int book[1300][130][70];
int sum = 0;
int bfs(int x, int y, int z)
{
int ans = 1;
queue<Node> q;
q.push({ x,y,z });
while (!q.empty()) {
Node node = q.front();
q.pop();
//遍历六个方向
for (int i = 0; i < 6; i++) {
int new_x = node.x + dx[i];
int new_y = node.y + dy[i];
int new_z = node.z + dz[i];
if (new_x < 0 || new_x >= M || new_y < 0 || new_y >= N || new_z < 0 || new_z >= L || book[new_x][new_y][new_z] == 1 || f[new_x][new_y][new_z] == 0)
continue;
ans++;
book[new_x][new_y][new_z] = 1;
q.push({ new_x,new_y,new_z });
}
}
if (ans >= T) return ans;
else return 0;
}
int main()
{
cin >> M >> N >> L >> T;
for (int i = 0; i < L; i++)
for (int j = 0; j < M; j++)
for (int k = 0; k < N; k++)
cin >> f[j][k][i];
for (int i = 0; i < L; i++)
for (int j = 0; j < M; j++)
for (int k = 0; k < N; k++)
if (f[j][k][i] == 1 && book[j][k][i] == 0) {
book[j][k][i] = 1;
sum += bfs(j, k, i);
}
cout << sum << endl;
return 0;
}没有AC的代码(调了很久,还是2/30)。
只有一个点2分,其他点都是运行超时或者内存超限。将BFS的倒数第七句的[tz][tz][ty]改成[tz][tx][ty]还是只有6分。又发现错误的大佬可以指正一下。
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int M, N, L, T;
int f[61][1287][130];
bool visited[61][1287][130];
//上下前后左右六个方向
int dx[6] = { 0,0,-1,1,0,0 };
int dy[6] = { 0,0,0,0,-1,1 };
int dz[6] = { -1,1,0,0,0,0 };
struct coord {
int x, y, z;
};
int bfs(int x_, int y_, int z_)
{
int ans = 1;
queue<coord> q;//{z,x,y}
coord p = { x_,y_,z_ };
q.push(p);
visited[z_][x_][y_] = 1;
while (!q.empty()) {
coord cur = q.front();
q.pop();
int x = cur.x;
int y = cur.y;
int z = cur.z;
for (int i = 0; i < 6; i++) {
int tx = x + dx[i];
int ty = y + dy[i];
int tz = z + dz[i];
if (tx >= 0 && tx < M && ty >= 0 && ty < N && tz >= 0 && tz < L && visited[tz][tx][ty] == false && f[tz][tx][ty] == 1) {
coord adj = { tx,ty,tz };
q.push(adj);
visited[tz][tz][ty] = 1;
ans++;
}
}
}
return ans;
}
int main()
{
cin >> M >> N >> L >> T;
for (int i = 0; i < L; i++) {
for (int j = 0; j < M; j++) {
for (int k = 0; k < N; k++) {
cin >> f[i][j][k];
}
}
}
int sum = 0;
/*
int sum1 = sizeof(f) / sizeof(int);
int sum2 = sizeof(visited) / sizeof(int);
cout << sum1 << endl << sum2 << endl;
*/
for (int i = 0; i < L; i++) {
for (int j = 0; j < M; j++) {
for (int k = 0; k < N; k++) {
if (visited[i][j][k] == 1 || f[i][j][k] == 0) continue;
int v = bfs(i, j, k);
sum += (v >= T ? v : 0);
}
}
}
cout << sum;
}7-10 图着色问题
题目
分数 25
作者 陈越
单位 浙江大学
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式:
输入在第一行给出3个整数V(0<V≤500)、E(≥0)和K(0<K≤V),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,给出了一个正整数N(≤20),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。
输出格式:
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
输入样例:
6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4
输出样例:
Yes
Yes
No
No
代码长度限制
16 KB
时间限制
300 ms
内存限制
64 MB
思路
以此判断每个点是否有颜色相同的相邻点。甚至不用搜索。
关键点是每一个方案颜色只能有K种(刚好K种)。
AC代码
//只用k种颜色,不多不少
#include<iostream>
#include<vector>
#include<map>
#include<queue>
using namespace std;
int V,E,K;
vector<vector<int>> g;
int color[502];
int main()
{
cin>>V>>E>>K;
g.resize(V+1);
for(int i=0;i<E;i++){
int x,y;
cin>>x>>y;
g[x].emplace_back(y);
g[y].emplace_back(x);
}
int n;
cin>>n;
while(n--){
map<int,int> mp;
for(int i=1;i<=V;i++){
cin>>color[i];
mp[color[i]]++;
}
int color_cnt=mp.size();
if(color_cnt!=K){
cout<<"No\n";
continue;
}
bool flag=true;
for(int i=1;i<=V;i++){
for(int j=0;j<g[i].size();j++){
if(color[i]==color[g[i][j]]){
flag=false;
goto loop;
}
}
}
loop:;
if(flag) cout<<"Yes\n";
else cout<<"No\n";
}
}7-11 拯救007
分数 25
作者 陈越
单位 浙江大学
在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。)
设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。
输入格式:
首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。
输出格式:
如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
输入样例 1:
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12
输出样例 1:
Yes
输入样例 2:
4 13
-12 12
12 12
-12 -12
12 -12
输出样例 2:
No
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
思路
用BFS判断能不能走到鳄鱼池旁边即可。
两个点相邻的依据。两个点的距离<=D。
输入时将所有能在池心岛一脚跳过去的点入队。文章来源:https://www.toymoban.com/news/detail-856507.html
AC代码
#include<iostream>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
int N, D;
int book[110];
struct Node {
int x, y;
int i;
};
queue<Node> q;
vector<Node> g;
bool flag = false;
void bfs()
{
while (!q.empty()) {
Node node = q.front();
q.pop();
for (int i = 0; i < N; i++) {
if (book[i] == 1 || i == node.i) continue;
int dx = abs(g[i].x - node.x);
int dy = abs(g[i].y - node.y);
int dis = dx * dx + dy * dy;
if (dis <= D * D) {
q.push(g[i]);
book[i] = 1;
int minedgex = min(abs(g[i].x - 50), abs(g[i].x + 50));
int minedgey = min(abs(g[i].y - 50), abs(g[i].y + 50));
if (minedgex <= D || minedgey <= D) { flag = true; return; }
}
}
}
}
int main()
{
cin >> N >> D;
double maxdis = (7.5 + D) * (7.5 + D);
//处理输入,先将能从池心岛一步跳往的点入队
for (int i = 0; i < N; i++) {
int x, y;
cin >> x >> y;
g.push_back({ x,y,i });
if (x * x + y * y <= maxdis) {
q.push({ x,y,i });
book[i] = 1;
//该点距离鳄鱼池左右边界的最短距离
int minedgex = min(abs(x - 50), abs(x + 50));
//该点距离鳄鱼池上下边界的最短距离
int minedgey = min(abs(y - 50), abs(y + 50));
if (minedgex <= D || minedgey <= D) { flag = true; }
}
}
if(!flag) bfs();
if (flag) cout << "Yes";
else cout << "No";
}//文章来源地址https://www.toymoban.com/news/detail-856507.html
到了这里,关于PTA图论的搜索题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!