贪心算法在找零问题中的应用-Toy模板网

这篇具有很好参考价值的文章主要介绍了贪心算法在找零问题中的应用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

引言

找零问题是一个经典的优化问题，其目标是用最少的硬币找零给定的金额。贪心算法是解决这类问题的一种常用方法，其核心思想是在每一步选择中都采取最好或最优（即最有利）的选择，从而希望能够导致全局的最好或最优的解。在找零问题中，贪心算法的策略通常是根据硬币面额从大到小进行选择。

本文将围绕找零问题展开，通过贪心算法设计解决方案，并证明在特定条件下贪心算法的有效性。同时，也将探讨贪心算法失效的情况，并设计一种通用的找零算法。

贪心算法在找零问题中的应用,c/c++,贪心算法,算法,c语言,排序算法,c++

a. 贪心算法求解找零问题

算法设计

假设我们有25美分、10美分、5美分和1美分四种面额的硬币。贪心算法的策略是尽可能多地使用面额较大的硬币，以减少硬币的总数。

初始化找零金额n。
如果n大于等于25美分，则从n中减去25美分，并增加25美分硬币的数量。
如果n大于等于10美分且小于25美分，则从n中减去10美分，并增加10美分硬币的数量。
如果n大于等于5美分且小于10美分，则从n中减去5美分，并增加5美分硬币的数量。
如果n大于等于1美分且小于5美分，则从n中减去1美分，并增加1美分硬币的数量。
重复步骤2至5，直到n为0。

算法证明

要证明贪心算法在这种情况下能找到最优解，我们需要证明使用贪心策略找零所用的硬币数量是最少的。

假设存在一种更优的找零方式，它使用的硬币数量比贪心算法少。由于贪心算法总是优先使用面额较大的硬币，因此这种更优的方式必然在某个步骤中使用了比贪心算法更多的面额较小的硬币。然而，这会导致在后续步骤中可用的面额较大的硬币数量减少，从而需要更多的硬币来完成找零。这与假设更优的方式使用的硬币数量更少相矛盾。因此，贪心算法在这种情况下能找到最优解。

b. 硬币面额为c的幂时的贪心算法证明

算法设计

假设硬币面额是c的幂，即面额为C,c,…,C,c和k为整数，c>1,k≥1。在这种情况下，贪心算法依然优先使用面额较大的硬币。

算法证明

为了证明在这种情况下贪心算法总能得到最优解，我们可以使用数学归纳法。

基础情况：当k=1时，只有一种面额的硬币，贪心算法显然是最优的。

归纳假设：假设当k=m时，贪心算法是最优的。

归纳步骤：当k=m+1时，考虑使用贪心算法得到的找零方案。如果使用的最大面额的硬币数量为0，那么问题退化为k=m的情况，根据归纳假设，贪心算法是最优的。否则，如果我们使用至少一个最大面额的硬币，那么剩余的找零金额可以使用k=m的贪心算法来解决。由于归纳假设，这个子问题也是最优的。因此，当k=m+1时，贪心算法是最优的。

由数学归纳法，我们得出结论：当硬币面额为c的幂时，贪心算法总能得到最优解。

c. 设计使贪心算法失效的硬币面额组合

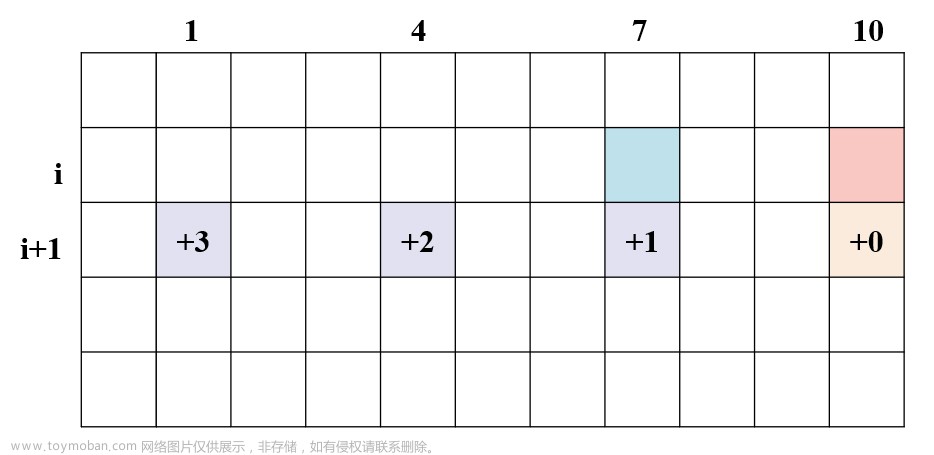
要使贪心算法不能保证得到最优解，我们需要设计一组特殊的硬币面额。一种常见的例子是使用1美分、3美分和4美分三种硬币。考虑找零7美分的情况，贪心算法会选择4美分和3美分，共需要两枚硬币。然而，最优解是使用两枚3美分硬币和一枚1美分硬币，共需要三枚硬币。因此，在这种情况下，贪心算法不能保证得到最优解。

d. 通用找零算法设计

算法设计

为了设计一个适用于任何k种不同面额硬币的通用找零算法，我们可以使用动态规划的方法。假设硬币面额为coins[k]，找零金额为n。

初始化一个大小为n+1的数组dp，其中dp[i]表示找零金额为i时所需的最少硬币数量。
对于每个金额i（从1到n），遍历所有硬币面额coins[j]，如果coins[j]小于等于i，则更新dp[i]为dp[i-coins[j]]+1和dp[i]中的较小值。
返回dp[n]作为找零所需的最少硬币数量。

算法实现（伪代码）

function minCoins(coins, n):
    dp = array of size n+1 filled with ∞
    dp[0] = 0
    for i from 1 to n:
        for j from 0 to k-1:
            if coins[j] <= i:
                dp[i] = min(dp[i], dp[i-coins[j]] + 1)
    return dp[n]

算法实现（C代码）

#include <stdio.h>
#include <limits.h>

int minCoins(int coins[], int k, int n) {
    int dp[n+1];
    for (int i = 0; i <= n; i++) {
        dp[i] = INT_MAX;
    }
    dp[0] = 0;
    
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < k; j++) {
            if (coins[j] <= i) {
                dp[i] = fmin(dp[i], dp[i-coins[j]] + 1);
            }
        }
    }
    
    return dp[n];
}

int main() {
    int coins[] = {1, 3, 4};
    int k = sizeof(coins) / sizeof(coins[0]);
    int n = 7;
    printf("Minimum coins needed: %d\n", minCoins(coins, k, n));
    return 0;
}

结论

贪心算法在找零问题中是一种有效的策略，特别是在硬币面额为c的幂的情况下，它总能找到最优解。然而，当硬币面额不满足特定条件时，贪心算法可能会失效。为了处理更一般的情况，我们可以使用动态规划的方法设计一个通用的找零算法，该算法能够在任何硬币面额组合下找到最优解。文章来源地址https://www.toymoban.com/news/detail-856569.html

到了这里，关于贪心算法在找零问题中的应用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！