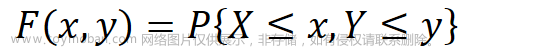统计思维系列课程03：随机变量及其分布

随机变量

在相同的条件下，如果每次试验可能出现这样或那样的结果，我们对随机事件进行数量化，用 X 表示所有可能的事件，也就是说 X 可以有不同的取值，用 P(X) 表示 X 取不同的值时对应事件发生的概率，如果我们把 P(X) 称作概率函数（probability function），那么这里的 X 就称为概率函数 P(X) 的随机变量（random variable）。

下面是一些随机变量的例子：

1. 掷一颗骰子，出现的点数是一个随机变量。
2. 检查100件产品，残次品的数量是一个随机变量。
3. 某电商网站今年的销售额是一个随机变量。

简单的说，随机变量的值是需要通过试验来进行确认的。随机变量根据其值是否可列分为：

• 离散型随机变量（discrete random variable）：随机变量 X 所有的取值可以逐个列出，例如：一批产品中取到残次品的个数、客服系统单位时间内收到电话呼叫的次数等。
• 连续型随机变量（continuous random variable）：随机变量 X 所有的取值无法逐个列出，例如：一批电子元器件的寿命、测量误差等。

说明：如果离散型随机变量的取值非常庞大时，可以近似看做连续型随机变量。

如上图2所示，由于连续型随机变量可以取某个区间或整个实数轴上任意的值，我们不能够像离散型随机变量那样列出每一个值及其对应的概率，我们可以定义概率密度函数（probability density function）和分布函数（distribution function）来描述其概率。概率密度函数满足以下两个条件：

(1)f(x)≥0(2)∫−∞+∞f(x)dx=1需要注意的是， f(x) 并不是一个概率，在指定范围对 f(x) 进行积分的结果才是概率，例如随机变量 X 取值在 a 和 b 之间的概率是：

(3)P(a<X<b)=∫abf(x)dx对于连续型随机变量，由于不可能去罗列出每一个值出现的概率，为此我们需要引入分布函数的概念，如下所示：(4)F(x)=P{X≤x}=∫−∞xf(t)dt如果将 X 看成是数轴上的随机坐标，上面的分布函数表示了 X 落在区间 (−∞,x) 中的概率。很显然，分布函数有以下性质：

1. F(x) 是一个单调不减的函数；
2. 0≤F(x)≤1 ，且 F(−∞)=limx→−∞F(x)=0 ， F(∞)=limx→∞F(x)=1 ；
3. F(x) 是右连续的。

按照分布函数的定义，上面的 P(a<X<b) 也可以写成：(5)P(a<X<b)=F(b)−F(a)期望和方差

为了全面了解随机变量 X 的概率性质，最好的情况是知道 X 的概率分布。但在现实问题中， X 的概率分布往往不好确定，但是在很多场景下，我们也不需要了解 X 所有的概率性质，只需要知道它某些数字特征就够了。在随机变量的各种数字特征中，最为重要的就是（数学）期望和方差。

• 期望：表示随机变量平均水平或集中程度的数字特征，是随机变量按照概率的加权平均值，记为 E(X) 。
  • 对于离散型随机变量 X ，若 ∑i=1∞xipi 收敛，那么它就是随机变量 X 的期望。
    (6)E(X)=∑i=1∞xipi
  • 对于连续型随机变量 X ，其概率密度函数为 f(x) ，若 ∫−∞∞xf(x)dx 收敛，那么它就是随机变量 X 的期望(7)E(x)=∫−∞∞xf(x)dx
• 方差：方差是表示随机变量变异程度或离散程度的数字特征，它是随机变量与其数学期望离差的平均水平。对于随机变量 X ，若 E[X−E(X)]2 存在，则称 E[X−E(X)]2 为 X 的方差，常用记为 D(X) 或 Var(X) 。
  • 离散型随机变量 X 的方差：
    (8)Var(X)=∑i=1∞[xi−E(X)]2pi
  • 连续型随机变量 X 的方差：(9)Var(X)=∫−∞∞[x−E(X)]2f(x)dx
• 期望与方差的性质：
  • 对于任意两个随机变量 X1 和 X2 ，则有 E(X1+X2)=E(X1)+E(X2) 。
  • 若 X 是随机变量， a 和 b 是任意常量，则有 E(aX+b)=aE(X)+b 和 Var(aX+b)=a2Var(X) 。
  • 若随机变量 X1 和 X2 独立，则有 Var(X1+X2)=Var(X1)+Var(X2) 。

离散型随机变量的分布

• 伯努利分布（Bernoulli distribution）：又名两点分布或者0-1分布，是一个离散型概率分布。若伯努利试验（只有两种可能结果的单次随机试验）成功，则随机变量取值为1。若伯努利试验失败，则随机变量取值为0。记其成功概率为 p(0≤p≤1) ，则失败概率为 1−p ，则概率质量函数为：
  (10)P(X=k)=pk(1−p)1−k={p(k=1)1−p(k=0)
• 二项分布（binomial distribution）：二项分布描述了 n 重伯努利试验中，如果每次试验成功的概率为 p ，正好有 k 次成功的概率分布。一般地，如果随机变量 X 服从参数为 n 和 p 的二项分布，记为 X∼B(n,p) ，其概率质量函数为：
  (11)P(X=k)=(nk)pk(1−p)n−k
  注意：上面提到的 n 重伯努利试验需要满足以下要求：①试验的结果只有两种：成功或失败；②试验的结果是独立的，彼此不影响；③试验重复次数是固定的n；④每次试验成功的概率都是p。在上面的公式中， (nk) 表示 n 选 k 的组合数，国内的教科书通常记为 Cnk ，计算公式为 n!k!(n−k)! 。Python中，可以通过math模块的comb函数计算组合数的值；可以通过三方库 numpy 中的random.binomial函数产生二项分布的随机数；可以通过三方库 scipy 中的stats.binom.pmf函数计算二项分布的概率。Excel 中，可以通过BINOM.DIST函数计算二项分布的概率。

很显然，伯努利分布就是二项分布在 n=1 时的特例。二项分布的期望和方差分别是：(12)E(X)=npVar(X)=np(1−p)

• 泊松分布（Poisson distribution）：泊松分布通常用来描述指定的时间范围或指定的面积（体积）内随机事件发生次数的概率分布，例如：某台服务器在一定时间内接收到服务请求的次数、单位时间内汽车站台的候客人数、某种机器每月出现故障的次数、某区域每年发生自然灾害的次数、DNA序列的变异数、放射性原子核的衰变数、保险公司每天收到死亡声明的份数等。泊松分布的概率质量函数如下所示：
  (13)P(X=k)=e−λλkk!其中，参数 λ 是单位时间或单位面积（体积）内事件的平均值。

说明：上面两张图都来自于维基百科，我们也可以用 Python 的三方库 matplotlib 来绘制上面的图形，需要代码的小伙伴可以在评论区留言。

泊松分布的期望和方差分别为：

(14)E(X)=λVar(X)=λ

说明：在没有计算机的年代，由于二项分布的运算量太大，为了减少运算量，数学家们通常用泊松分布作为二项分布的近似。当二项分布的 n 很大， p 很小的时候，我们可以令 λ=np ，然后用泊松分布的概率质量函数计算概率来近似二项分布的概率。例如：某批集成电路的次品率为0.15%，随机抽取1000块该集成电路，求次品数分别为0、1、2、3、4、5的概率。很显然，这里提到的场景是一个 n 重伯努利试验，由于 n=1000 ， p=0.0015 ，可以用泊松分布做近似，这里大家也能够很直观的感受到泊松分布的计算量是远远小于二项分布的，下面的表格是二项分布和泊松分布结果的对照。

说明：使用 Python 语言，可以通过三方库 scipy 中的 stats.poisson.pmf函数计算泊松分布的概率。Excel 中，可以通过 POISSON.DIST函数计算泊松分布的概率。

• 几何分布（geometric distribution）：几何分布通常用来描述在伯努利试验中，获得一次成功需要的试验次数。如果每次试验成功的概率为 p ，那么 k 次试验，第 k 次才得到的成功的概率是： P(X=k)=(1−p)k−1p ，其中 k=1,2,3,⋯ 。若随机变量 X 服从参数为 p 的几何分布，则记为 X∼G(p) 。

几何分布的期望和方差分别为：

(15)E(X)=1pVar(X)=1−pp2

例子

下面，我们通过一些例子来展示，如何在特定场景下利用上面的概率质量函数完成概率计算。

例1：已知某城市餐饮行业首年的生存率为20%，假设今年有15家餐馆开业，问1年后至少有4家餐馆存活下来的概率是多少？

可以简单评估一下，存活下来的餐馆数量应该是一个二项分布的随机变量。现在已知 n=15,p=0.2，我们可以通过下面的公式来计算题目要求的概率(16)P(X≥4)=1−P(x<4)=1−∑k=03Cnkpk(1−p)n−k=1−∑k=03C15i×0.2i×0.815−i≈1−0.6482≈0.3518

提示：使用 Python 语言，可以利用三方库 scipy 的 stats模块来完成上面的计算，执行 stats.binom.cdf(3, n=15, p=0.2)可以得到0.6482，其中 cdf函数是 cumulative distribution function的缩写，允许我们设定随机变量的值以及二项分布的参数 n 和 p ，来计算累积概率分布。

例2：一个赌博游戏，每局获胜的概率是10%，玩家需要玩多少次才能大概率（95%的概率）保证赢一次？（专栏导读中“有趣的概率问题”中的第9题）

题目要求的随机变量 X 服从几何分布，如果希望95%的概率获胜一次，也就意味着：(17)P(X≤k)=1−P(X>k)=1−(1−p)k≥0.95我们将 p=0.1 代入上面的不等式，得到 k>28 ，即玩家需要玩29次才能大概率保证赢一次，这个结果是不是颠覆了你的认知。同理，如果面试获得offer的概率是50%，如果要以95%的概率获得offer，至少需要面试5次。但是，如果我们通过提升自己的综合职业素养，让面试成功获得offer的概率提升到78%，这个时候面试2次就有95%以上的概率能获得offer。就找工作这个事情而言，几何分布告诉我们，成功获得offer的秘密就是要么你得多约面试，要么你得提升自己的综合职业素养，前者得靠自己，后者的话我可以帮到你，这也是我现在正在从事的工作。

提示：使用 Python 语言，可以利用三方库 scipy 的 stats模块来完成上面的计算，执行 stats.geom.ppf(0.95, 0.1)可以得到29，其中 ppf函数是 percent point function的缩写，允许我们设定累积分布概率和试验成功的概率来获得随机变量的值。

例3：假设一个公司门口有10个停车位，该公司有100名员工上班，每名员工早上8点钟之前开车来上班的概率是10%，这些人每天什么时候来公司是随机的，而且彼此无关，也不存在头一天来晚了没有抢到车位第二天就早到的可能性。问早上8点整开车到了公司，停车场还有车位的概率是多少？

按照题目所述，停车场一共有10个车位，那就意味着早上8点以前，只要停车场停车的数量为0到9，8点整开车到公司就是有车位的。停车场在早上8点以前有多少量车是一个服从泊松分布的随机变量，我们令 λ=np ，其中 n 是员工的数量， p 是8点钟以前开车来上班的概率，因此 λ=100×0.1=10 。接下来，我们可以用下面的公式计算出题目中的概率：

(18)∑k=09P(X=k)=∑k=09e−λλkk!=∑k=09e−1010kk!=0.4579

提示：使用 Python 语言，可以利用三方库 scipy 的 stats模块来计算泊松分布的累积概率，执行 stats.poisson.cdf(9, 10)就可以得到0.4579。

如果我们希望把上面的概率提高到0.9，也就是说早上8点整开车到公司会大概率有车位，停车场需要大规模扩容吗？利用上面的公式，我们可以计算出，在其他条件不变的情况下，当停车场有15个车位时，这个概率就会大于0.9。

连续型随机变量的分布

在众多连续型随机变量中，最重要的一种随机变量其概率密度函数呈现铃铛形状。我们把这种随机变量称之为正态随机变量，相应的概率分布称为正态分布（normal distribution）或高斯分布（Gaussian distribution）。正态分布经常用于自然科学和社会科学中来代表一个分布不明的随机变量，事实上，如果一个随机变量的值受到诸多因素的影响，但是每个因素的影响又非常有限，那么该随机变量最终会呈现出正态分布。这一点，从定性的角度可以通过伽尔顿板试验来得到验证，如下图所示。

伽尔顿板为一块竖直放置的板，上面有交错排列的钉子。让小球从板的上端自由下落，当其碰到钉子后会随机向左或向右落下。最终，小球会落至板底端的某一格子中。假设板上共有 n 排钉子，每个小球撞击钉子后向右落下的概率为 p （如果向左向右的概率相同， p 的取值为0.5），那么小球落入下方第 k 个格子概率服从上面讲过的二项分布，其概率值为 (nk)pk(1−p)n−k 。此时，将大量小球落至格中，格子中的小球数量将呈现出正态分布的铃铛型曲线。这里，小球落入不同的格子相当于随机变量取到不同的值，而钉子就是影响随机变量值的因素，小球落入哪个格子受到了多行钉子的影响，不管做多少次这样的试验，最终格子中小球的数量都呈现出正态分布的轮廓。

如果随机变量 X 的概率密度函数为：

(19)f(x)=12πσe−(x−μ)22σ2

则称 X 服从正态分布，记为 X∼N(μ,σ2) ，其中 μ 是正态分布的位置参数，它决定了概率密度曲线对称轴的位置； σ 是正态分布的形状参数，它决定了概率密度曲线的陡缓程度，如下图所示。

当正态分布的两个参数 μ=0 ， σ=1 时，有：

(20)f(x)=12πe−x22我们将这样的正态分布称为标准正态分布（standard normal distribution）。一个普通的正态分布可以通过下面的线性变换转化为标准正态分布，这样的话就可以通过查表的方式解决正态分布的概率计算问题，在计算机技术普及之前，这一点是相当重要的。

(21)Z=X−μσ∼N(0,1)

说明：今天由于计算机的普及，上面的标准正态分布速查表就没有那么重要了。如果你使用 Python语言，可以通过三方库 scipy 中的 stats.norm.pdf函数计算正态分布的概率。Excel 中，可以通过 NORM.DIST函数计算正态分布的概率，可以通过 NORM.S.DIST计算标准正态分布的概率。

根据“棣莫弗-拉普拉斯积分定理”，假设 μn(n=1,2,⋯) 表示 n 重伯努利试验中成功的次数，已知每次试验成功的概率为 p，有：

(22)limn→∞P{μn−npnp(1−p)≤x}=12π∫−∞xe−t22dt该定理表明正态分布是二项分布的极限分布，这也是为什么说概率统计是建立在抛硬币试验基础上的最佳佐证。

68-95-99.7法则

提到正态分布，就必须说一下“3 σ 法则”，该法则也称为“68-95-99.7法则”，如下图所示。

说明：上面两张图也来自于维基百科，很多讲解正态分布的文章和视频都引用了这些图。

对于随机变量 X∼N(μ,σ2) ，上面的图也可以用下面的公式来表示：

(23)P(μ−σ<X<μ+σ)≈0.68P(μ−2σ<X<μ+2σ)≈0.95P(μ−3σ<X<μ+3σ)≈0.997简单的说，对于一个正态分布的随机变量，几乎所有（99.7%）的值都会在均值（ μ ）正负三个标准差（ σ ）的范围内。换句话说，如果我们认为某个数据来自于一个正态总体，那么它的值应该以极大的概率位于 [μ−3σ,μ+3σ] 范围或以较大概率位于 [μ−2σ,μ+2σ] 范围。如果数据不在这个范围，我们就有足够的理由怀疑它并非来自于该正态总体，这一点对于我们后面要讲的假设检验非常重要。生产中的质量检验和过程控制也利用了这一思想，有兴趣的读者可以了解一下风靡全球的六西格玛质量管理体系。在这种质量管理体系下，产品的合格率要达到99.9999998%，即残次率仅为十亿分之二；即便考虑到1.5 σ 的漂移（由于随机因素的影响，实际结果偏离理论值的情况），残次率也仅为百万分之3.4，即100万个产品中有缺陷的产品不到4个。

我们再来讲一个大学英语四六级考试的例子，英语四六级考试的成绩并不是你卷面的原始分，而是经过处理之后的标准分。处理的方式是将所有人的考试成绩转化成一个 μ=500,σ=70 的正态分布，通过这个标准分你就能知道你的成绩在所有考生中所处的位置。很多学校设置的425分的合格线大致位于 μ−σ 的位置，通过上图可以看出，只要你的成绩大约超过了16%的考生，也就达到了合格的水平。这个要求其实并不高，只是很多人不明白学习英语的重要性，甚至以“爱国”来掩饰自己不重视英语的事实，这才导致了自己连16%这个水平都达不到。当然，每年考试也有不少人的成绩会超过640分，640分位于 μ+2σ 的位置，虽然这个成绩在很多学霸眼里不算什么，但已经是全国前2.5%的水平。美国纽约有一家对冲基金投资公司，这家公司非常擅长使用人工智能、机器学习、分布式计算等技术手段来进行投资策略的管理，它的名字叫 Two Sigma。这家公司的创始人之一大卫·赛格（David Siegel）是 MIT 的计算机博士，妥妥的 IT 技术男；而公司的名字据说是为了反映 Sigma 这个词的双重性，小写的 σ 指的是投资回报率相对于给定基准 μ 的波动性，而大写的 Σ 是指总的收益。当然，很多人更愿意相信，Two Sigma 这个名字是暗示基金的表现要达到 μ+2σ 这个水准，也就是近乎“百里挑二”的水平。

小结

最后我们留下两个小问题，大家可以思考一下，然后想想计算出的结果跟你平常的认知是不是有很大的出入。

1. 假设一架波音或空客的飞机是由50000个零件组成的，每个零件的可靠性是99.99%，在这样的品控下组装的飞机你敢去坐吗？（事实上，目前还有不少企业和它们的管理者对99.99%的可靠性感到非常乐观，这是多么可怕的事情！）
2. 如果你去玩摇骰子押大小的赌博游戏，如果已经连续开出了20次大，下一次你要不要梭哈，把所有的钱全部押小？（很多人对“随机”二字的理解都是有问题的，所以才会出现著名的赌徒谬误！）

另外，如果你熟悉 Excel 或 Python 语言，很多概率计算的问题都可以交给它们去处理，现在概率统计的教科书也不需要再像我们当前那样，在附录的部分放上各种各样的概率速查表。计算机以及人工智能的出现都是为了将人类从繁琐乏味的劳动中解放出来，对于这样的工具我们不应该感到焦虑，而是要用好它们来解放自己，让自己有更多的时间和精力去进行创造性的劳动。文章来源地址https://www.toymoban.com/news/detail-856597.html

到了这里，关于统计思维系列课程03：随机变量及其分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！