LeetCode 面试打卡 4: 动态规划 - DataWhale 导学-Toy模板网

这篇具有很好参考价值的文章主要介绍了LeetCode 面试打卡 4: 动态规划 - DataWhale 导学。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

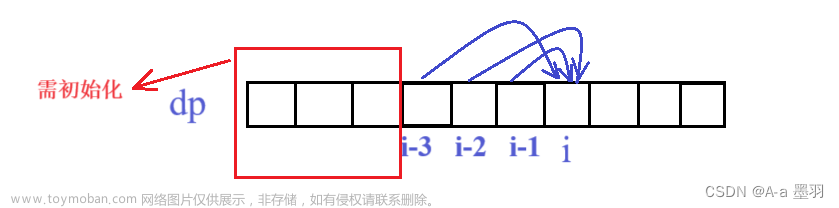
动态规划代码实现需要注意的问题

数组dp的初始化大小不正确，需要根据题目中所给的数据确定好dp数组的大小。一般为[m,n]即可
数组dp的初始化逻辑有误：根据题目条件，初始化dp数组
状态转移方程不正确：根据题目中的变量设定状态转移方程。

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出:5
解释:在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

一次遍历完成，最大盈利的计算，同时记录 minPrice最小价格和maxProfit最大利润的两个变量。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        # 设定初始变量 
        minPrice = inf
        maxProfit = 0
        # 进行遍历
        for price in prices:
            maxProfit = max(maxProfit,price-minPrice)
            minPrice = min(minPrice,price)

        return maxProfit

买卖股票2，

方法1:

因为可以交易多次，所以抓住所有上涨的趋势进行买入卖出就可以了。

方法2(动态规划):

动态规划 dp[i][0] 没有股票持有的最大利润 dp[i][1] 持有股票拥有的最大利润

没有持有股票的转移方程

$d p [i] [0] = ma x (d p [i - 1] [0], d p [i - 1] [1] + p r i ce [i])$

持有股票的动态规划方程

$d p [i] [1] = ma x (d p [i - 1] [1], d p [i - 1] [0] - p r i ce [i])$

class Solution:
    def maxProfit(self, prices):
        n = len(prices)
        dp = [[0 for _ in range(2)] for _ in range(n)]
        dp[0][0] = 0
        dp[0][1] = -prices[0]
        for i in range(1, n):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
        return dp[n - 1][0]

1143. 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ，它的长度为 3

使用动态规划求解,设定dp数组 dp[n][m],n,m分别为两个字符串的长度。

dp[n][m]也就表示s1[:i]和s2[:j]这两个子字符串的最大公共子序列长度。

设置i,j分别为s1,s2子字符串各自的长度.

状态转移方程

$s_1[i]=s_2[j]:dp[i][j]=dp[i-1][j-1]+1$

$s_1[i]!=s_2[j]:dp[i][j] =max(dp[i-1][j],dp[i][j-1])$

初始状态

i=0时dp[i][j]=0

j=0时dp[i][j]=0

代码:

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 定义dp数组 初始状态
        n,m = len(text1),len(text2)
        dp= [[0]*(m+1)  for _ in range(n+1)]

        # 完善动态规划数组
        for i in range(1,n+1):
            for j in range(1,m+1):
                if text1[i-1] == text2[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i][j-1],dp[i-1][j])
        return dp[n][m]

64. 最小路径和

给定一个包含非负整数的 mxn 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明每次只能向下或者向右移动一步。文章来源地址https://www.toymoban.com/news/detail-856946.html

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dp = [[0]*n for _ in range(m)]  # 修正了dp数组的大小

        dp[0][0] = grid[0][0]
        for i in range(1, m):  # 初始化第一列
            dp[i][0] = dp[i-1][0] + grid[i][0]
        for j in range(1, n):  # 初始化第一行
            dp[0][j] = dp[0][j-1] + grid[0][j]

        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]  # 使用min寻找最小路径和

        return dp[m-1][n-1]