一、最小生成树-prim算法
1.1 最小生成树概念
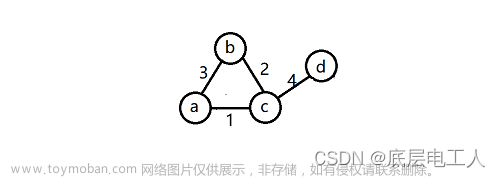
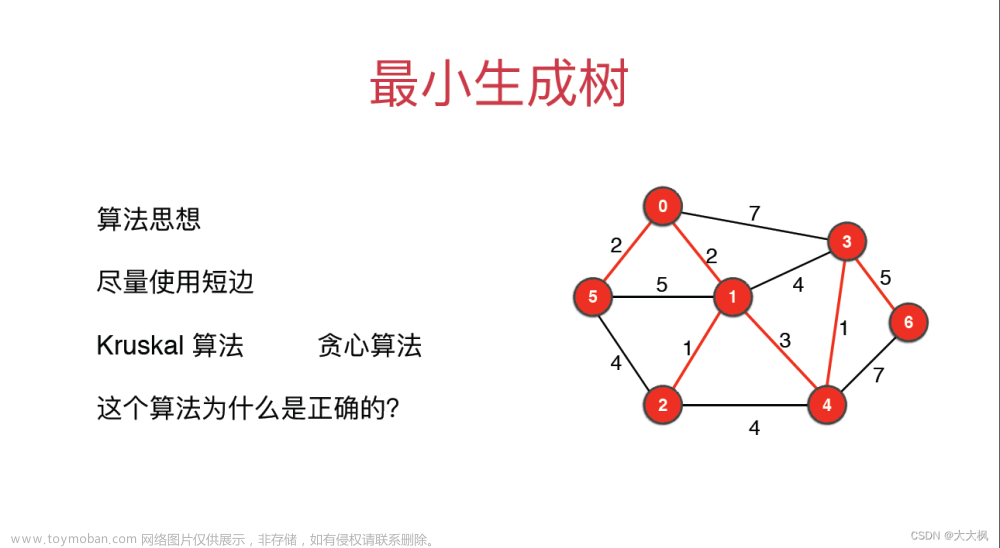
一幅图可以有很多不同的生成树,比如下面这幅图,红色的边就组成了两棵不同的生成树:
对于加权图,每条边都有权重(用最小生成树算法的现实场景中,图的边权重一般代表成本、距离这样的标量),所以每棵生成树都有一个权重和。比如上图,右侧生成树的权重和显然比左侧生成树的权重和要小。
那么最小生成树很好理解了,所有可能的生成树(包含所有顶点)中,权重和最小的那棵生成树就叫「最小生成树」。
1.2 稠密图-朴素prim
和djikstra很像
const int INF = 0x3f3f3f3f; // 定义一个非常大的数,用作无穷远的初始化值
int n; // n表示图中的顶点数
int g[N][N]; // 邻接矩阵,用于存储图中所有边的权重
int dist[N]; // 用于存储其他顶点到当前最小生成树的最小距离
bool st[N]; // 用于标记每个顶点是否已经被加入到最小生成树中
// Prim算法的实现,返回最小生成树的总权重
int prim() {
memset(dist, 0x3f, sizeof dist); // 初始化所有顶点到MST的距离为无穷远
int res = 0; // 存储最小生成树的总权重
for (int i = 0; i < n; i++) { // 主循环,每次添加一个顶点到MST
int t = -1; // 用于找到当前未加入MST且dist最小的顶点
for (int j = 1; j <= n; j++) // 遍历所有顶点,找到t
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
//t就是当前加入最小生成树的顶点
if (i && dist[t] == INF) return INF; // 如果图不连通,则返回INF
if (i) res += dist[t]; // 非首次迭代时,累加到MST的距离
st[t] = true; // 将顶点t加入到MST中
//再从T出发,更新所有未加入顶点到T的距离,用于下一轮新的T的更新
for (int j = 1; j <= n; j++) // 更新其他所有顶点到MST的最小距离
if (!st[j]) dist[j] = min(dist[j], g[t][j]);
}
return res; // 返回最小生成树的总权重
}
例题:

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 510,M = 100010,INF = 0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];
bool used[N];
int prim(){
memset(dist,0x3f,sizeof dist);
int res = 0;
for(int i = 0;i < n;i++){
int t = -1;
for(int j = 1;j <= n; j++){
if((!used[j]) && (t == -1 || dist[t] > dist[j]))
t = j;
}
used[t] = true;
//第一步的dist[t]为INF
if(i && dist[t] == INF) return INF;
if(i)res += dist[t];
for(int j = 1;j <= n;j++){
if(!used[j])
dist[j] = min(dist[j],g[t][j]);
}
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
//重要
memset(g,0x3f,sizeof(g));
for(int i = 0;i < m; i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
g[u][v] = g[v][u] = min(g[u][v],w);
}
int r = prim();
if(r == INF)puts("impossible");
else printf("%d",r);
return 0;
}1.3 堆优化的prim-不常用,且复杂,一般用kruskal替代
省略
二、最小生成树-kruskal算法
1.并查集复习
1.1 并查集(Union-Find)算法
是一个专门针对「动态连通性」的算法,我之前写过两次,因为这个算法的考察频率高,而且它也是最小生成树算法的前置知识
动态连通性
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:

这里所说的「连通」是一种等价关系,也就是说具有如下三个性质:
1、自反性:节点 p 和 p 是连通的。
2、对称性:如果节点 p 和 q 连通,那么 q 和 p 也连通。
3、传递性:如果节点 p 和 q 连通,q 和 r 连通,那么 p 和 r 也连通。
现在我们的 Union-Find 算法主要需要实现这三个 API:
class UF {
public:
/* 将 p 和 q 连接 */
void union(int p, int q);
/* 判断 p 和 q 是否连通 */
bool connected(int p, int q);
/* 返回图中有多少个连通分量 */
int count();
};函数功能说明:
比如说之前那幅图,0~9 任意两个不同的点都不连通,调用 connected 都会返回 false,连通分量为 10 个。
如果现在调用 union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。
再调用 union(1, 2),这时 0,1,2 都被连通,调用 connected(0, 2) 也会返回 true,连通分量变为 8 个。

初始化:
怎么用森林来表示连通性呢?我们设定树的每个节点有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。比如说刚才那幅 10 个节点的图,一开始的时候没有相互连通,就是这样:

代码如下:
class UF {
// 记录连通分量
private:
int count;
// 节点 x 的父节点是 parent[x]
int* parent;
public:
/* 构造函数,n 为图的节点总数 */
UF(int n) {
// 一开始互不连通
this->count = n;
// 父节点指针初始指向自己
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
/* 其他函数 */
};union实现:
操作如下:

代码如下:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
public:
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也一样
count--; // 两个分量合二为一
}
/* 返回某个节点 x 的根节点 */
int find(int x) {
// 根节点的 parent[x] == x
while (parent[x] != x)
x = parent[x];
return x;
}
/* 返回当前的连通分量个数 */
int count() {
return count;
}
};connected实现:
代码如下:
class UF {
private:
// 省略上文给出的代码部分...
public:
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
};1.2 平衡性优化-union优化
分析union和connected的时间复杂度,我们发现,主要 API connected和 union 中的复杂度都是 find 函数造成的,所以说它们的复杂度和 find 一样。
find 主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 logN,但这并不一定。logN 的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得「树」几乎退化成「链表」,树的高度最坏情况下可能变成 N。
图论解决的都是诸如社交网络这样数据规模巨大的问题,对于 union 和 connected 的调用非常频繁,每次调用需要线性时间完全不可忍受。
关键在于 union 过程,我们一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:

长此以往,树可能生长得很不平衡。我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。解决方法是额外使用一个 size 数组,记录每棵树包含的节点数,我们不妨称为「重量」:
class UF {
private:
int count;
int* parent;
// 新增一个数组记录树的“重量”
int* size;
public:
UF(int n) {
this->count = n;
parent = new int[n];
// 最初每棵树只有一个节点
// 重量应该初始化 1
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
/* 其他函数 */
};比如说 size[3] = 5 表示,以节点 3 为根的那棵树,总共有 5 个节点。这样我们可以修改一下 union 方法:
class UF {
private:
// 为了节约篇幅,省略上文给出的代码部分...
public:
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 小树接到大树下面,较平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
};
这样,通过比较树的重量,就可以保证树的生长相对平衡,树的高度大致在 logN 这个数量级,极大提升执行效率。
此时,find , union , connected 的时间复杂度都下降为 O(logN),即便数据规模上亿,所需时间也非常少。
1.3 路径压缩-find优化
其实我们并不在乎每棵树的结构长什么样,只在乎根节点。
因为无论树长啥样,树上的每个节点的根节点都是相同的,所以能不能进一步压缩每棵树的高度,使树高始终保持为常数?

这样每个节点的父节点就是整棵树的根节点,find 就能以 O(1) 的时间找到某一节点的根节点,相应的,connected 和 union 复杂度都下降为 O(1)。
要做到这一点主要是修改 find 函数逻辑,非常简单,但你可能会看到两种不同的写法。
方法1:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
private:
int find(int x) {
while (parent[x] != x) {
// 这行代码进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
};每次使得当前x指向父节点的父节点,这样会将一些节点向上移,然后缩短树的长度

压缩结束为:

方法二:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
// 第二种路径压缩的 find 方法
public:
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
};其迭代写法如下(便于理解):
int find(int x) {
// 先找到根节点
int root = x;
while (parent[root] != root) {
root = parent[root];
}
// 然后把 x 到根节点之间的所有节点直接接到根节点下面
int old_parent = parent[x];
while (x != root) {
parent[x] = root;
x = old_parent;
old_parent = parent[old_parent];
}
return root;
}最终效果:

1.4 并查集框架-优化后
class UF {
private:
// 连通分量个数
int count;
// 存储每个节点的父节点
int *parent;
public:
// n 为图中节点的个数
UF(int n) {
this->count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 将节点 p 和节点 q 连通
void union_(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
count--;
}
// 判断节点 p 和节点 q 是否连通
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 返回图中的连通分量个数
int count_() {
return count;
}
};2.kruskal
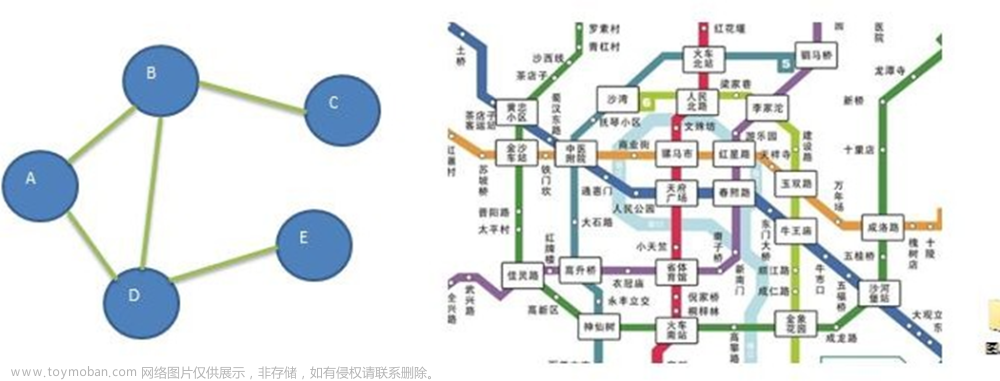
给你输入编号从 0 到 n - 1 的 n 个结点,和一个无向边列表 edges(每条边用节点二元组表示),请你判断输入的这些边组成的结构是否是一棵树。
如果输入:
n = 5
edges = [[0,1], [0,2], [0,3], [1,4]]这些边构成的是一棵树,算法应该返回 true:

输入:
n = 5
edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]形成的就不是树结构了,因为包含环:

我们思考为何会产生环?仔细体会下面两种添边的差别


总结一下规律就是:
对于添加的这条边,如果该边的两个节点本来就在同一连通分量里,那么添加这条边会产生环;反之,如果该边的两个节点不在同一连通分量里,则添加这条边不会产生环。
那么只需要在union两节点之前先检测两节点是否已经connection,如果已连接所有添加后会生成环,则返回false。同时需要注意count==1,不然就是森林了。
代码如下:
class UF {
public:
vector<int> parent;
UF(int n) {
for (int i = 0; i < n; i++) {
parent.push_back(i);
}
}
int find(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
void union_(int p, int q) {
int root_p = find(p);
int root_q = find(q);
parent[root_p] = root_q;
}
bool connected(int p, int q) {
int root_p = find(p);
int root_q = find(q);
return root_p == root_q;
}
int count() {
int cnt = 0;
for (int i = 0; i < parent.size(); i++) {
if (parent[i] == i) {
cnt++;
}
}
return cnt;
}
};
bool validTree(int n, vector<vector<int>>& edges) {
UF uf(n);
// 遍历所有边,将组成边的两个节点进行连接
for (auto edge : edges) {
int u = edge[0];
int v = edge[1];
// 若两个节点已经在同一连通分量中,会产生环
if (uf.connected(u, v)) {
return false;
}
// 这条边不会产生环,可以是树的一部分
uf.union_(u, v);
}
// 要保证最后只形成了一棵树,即只有一个连通分量
return uf.count() == 1;
}3.连接所有点的最小费用-kruskal算法
所谓最小生成树,就是图中若干边的集合(我们后文称这个集合为 mst,最小生成树的英文缩写),你要保证这些边:
1、包含图中的所有节点。
2、形成的结构是树结构(即不存在环)。
3、权重和最小。
有之前题目的铺垫,前两条其实可以很容易地利用 Union-Find 算法做到,关键在于第 3 点,如何保证得到的这棵生成树是权重和最小的。
这里就用到了贪心思路:
将所有边按照权重从小到大排序,从权重最小的边开始遍历,如果这条边和 mst 中的其它边不会形成环,则这条边是最小生成树的一部分,将它加入 mst 集合;否则,这条边不是最小生成树的一部分,不要把它加入 mst 集合。
以此题为例:
 此题虽然是使用kruskal算法,但是并不是直接套用,还要有一些值得注意的事项
此题虽然是使用kruskal算法,但是并不是直接套用,还要有一些值得注意的事项
1:我们要将题目中的给出点,转换为点组合并且将权重添加进去
在题中只给出一个点的坐标,我们需要想方法转换为两个点的链接,所以需要将每个点(两个坐标组合)转换为一个符号标记,在链接数组把相连的两个符号放一起就行了,很明显,我们使用0-n-1来记录每一个点是最合适的,不仅方便遍历也一目了然
因此有如下代码:
vector<vector<int>> edges;
for(int i =0;i < points.size();i++){
//此处不能写为int j = 0,这样会重复导致超时,根据求子集的思想,应该从j=i+1开始
for(int j = i+1;j < points.size();j++){
// if(i == j)continue;//因为j=i+1开始,所有不需要这句判断
int w1 = abs(points[i][0]-points[j][0]);
int w2 = abs(points[i][1]-points[j][1]);
edges.push_back({i,j,w1+w2});
}
}2:我们要对得到的数组进行排序,而且是对权重维度排序,这就需要我们利用lambda来自定义sort的排序方式了
有代码如下:文章来源:https://www.toymoban.com/news/detail-857118.html
sort(edges.begin(),edges.end(),[](const vector<int>& a,const vector<int>& b){
return a[2] < b[2];
});依照kruskal算法,可以写出如下完整代码:文章来源地址https://www.toymoban.com/news/detail-857118.html
class uf{
private:
int count;
vector<int> parent;
public:
uf(int n){
this->count = n;
// parent = new int[n];
parent.resize(n);
for(int i=0;i < n;i++){
parent[i] = i;
}
}
int find(int x){
if(parent[x]!=x)
parent[x] = find(parent[x]);
return parent[x];
}
void Union(int p,int q){
int rootp = find(p);
int rootq = find(q);
if(rootp == rootq)return;
parent[rootp] = rootq;
count--;
}
bool connection(int p,int q){
int rootp = find(p);
int rootq = find(q);
return rootp == rootq;
}
};
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
vector<vector<int>> edges;
for(int i =0;i < points.size();i++){
//此处不能写为int j = 0,这样会重复导致超时,根据求子集的思想,应该从j=i+1开始
for(int j = i+1;j < points.size();j++){
// if(i == j)continue;//因为j=i+1开始,所有不需要这句判断
int w1 = abs(points[i][0]-points[j][0]);
int w2 = abs(points[i][1]-points[j][1]);
edges.push_back({i,j,w1+w2});
}
}
sort(edges.begin(),edges.end(),[](const vector<int>& a,const vector<int>& b){
return a[2] < b[2];
});
uf uf(points.size());
int sum_w = 0;
for(auto& s : edges){
int q = s[0],p = s[1],w = s[2];
if(uf.connection(p,q))continue;
sum_w +=w;
uf.Union(p,q);
}
return sum_w;
}
};
到了这里,关于图论- 最小生成树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!