✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
物理应用 机器学习
🔥 内容介绍
斯图加特大学大地测量学和地理信息学硕士项目
该项目的核心思想是评估智能手机在海啸预警系统中的可用性。模拟了震级为 7 的地震的位移,并在数据中检测到了位移。
步骤 1:使用 Okada 程序模拟震级为 7 的地震的位移
步骤 2:根据模拟动作测量智能手机数据的动态运动的 GNSS 数据
步骤 3:通过卡尔曼滤波处理数据,检测 GNSS 数据中的智能手机位移
📣 部分代码
function varargout=okada85(varargin)%OKADA85 Surface deformation due to a finite rectangular source.% [uE,uN,uZ,uZE,uZN,uNN,uNE,uEN,uEE] = OKADA85(...% E,N,DEPTH,STRIKE,DIP,LENGTH,WIDTH,RAKE,SLIP,OPEN)% computes displacements, tilts and strains at the surface of an elastic% half-space, due to a dislocation defined by RAKE, SLIP, and OPEN on a% rectangular fault defined by orientation STRIKE and DIP, and size LENGTH and% WIDTH. The fault centroid is located (0,0,-DEPTH).%% E,N : coordinates of observation points in a geographic referential% (East,North,Up) relative to fault centroid (units are described below)% DEPTH : depth of the fault centroid (DEPTH > 0)% STRIKE : fault trace direction (0 to 360 relative to North), defined so% that the fault dips to the right side of the trace% DIP : angle between the fault and a horizontal plane (0 to 90)% LENGTH : fault length in the STRIKE direction (LENGTH > 0)% WIDTH : fault width in the DIP direction (WIDTH > 0)% RAKE : direction the hanging wall moves during rupture, measured relative% to the fault STRIKE (-180 to 180).% SLIP : dislocation in RAKE direction (length unit)% OPEN : dislocation in tensile component (same unit as SLIP)%% returns the following variables (same matrix size as E and N):% uN,uE,uZ : displacements (unit of SLIP and OPEN)% uZE,uZN : tilts (in rad * FACTOR)% uNN,uNE,uEN,uEE : horizontal strains POSITIVE = COMPRESSION (unit of FACTOR)%% Length unit consistency: E, N, DEPTH, LENGTH, and WIDTH must have the same% unit (e.g. km) which can be different from that of SLIP and OPEN (e.g. m) but% with a possible FACTOR on tilt and strain results (in this case, an% amplification of km/m = 1000). To have FACTOR = 1 (tilt in radians and% correct strain unit), use the same length unit for all aforesaid variables.%% [...] = OKADA85(...,NU) specifies Poisson's ratio NU (default is 0.25 for% an isotropic medium).%% Formulas and notations from Okada [1985] solution excepted for strain% convention (here positive strain means compression), and for the fault% parameters after Aki & Richards [1980], e.g.:% DIP=90, RAKE=0 : left lateral (senestral) strike slip% DIP=90, RAKE=180 : right lateral (dextral) strike slip% DIP=70, RAKE=90 : reverse fault% DIP=70, RAKE=-90 : normal fault%% It is also possible to produce partial outputs, with following syntax:% [uE,uN,uZ] = OKADA85(...) for displacements only;% [uE,uN,uZ,uZE,uZN] = OKADA85(...) for displacements and tilts;% [uE,uN,uZ,uNN,uNE,uEN,uEE] = OKADA85(...) for displacements and strains;% [uZE,uZN] = OKADA85(...) for tilts only;% [uZE,uZN,uNN,uNE,uEN,uEE] = OKADA85(...) for tilts and strains;% [uNN,uNE,uEN,uEE] = OKADA85(...) for strains only.%% Note that vertical strain components can be obtained with following equations:% uNZ = -uZN;% uEZ = -uZE;% uZZ = -(uEE + uNN)*NU/(1-NU);%% [...] = OKADA85(...,'plot') or OKADA85(...) without output argument% produces a 3-D figure with fault geometry and dislocation at scale (if% all of the fault parameters are scalar).%% Equations are all vectorized excepted for argument DIP which must be% a scalar (beacause of a singularity in Okada's equations); all other% arguments can be scalar or matrix of the same size.%% Example:%% [E,N] = meshgrid(linspace(-10,10,50));% [uE,uN,uZ] = okada85(E,N,2,30,70,5,3,-45,1,1,'plot');% figure, surf(E,N,uN)%% considers a 5x3 fault at depth 2, N30-strike, 70-dip, and unit dislocation% in all directions (reverse, senestral and open). Displacements are computed% on a regular grid from -10 to 10, and North displacements are plotted as a% surface.%%% Author: Franois Beauducel <beauducel@ipgp.fr>% Institut de Physique du Globe de Paris% Created: 1997% Updated: 2014-05-24%% References:% Aki K., and P. G. Richards, Quantitative seismology, Freemann & Co,% New York, 1980.% Okada Y., Surface deformation due to shear and tensile faults in a% half-space, Bull. Seismol. Soc. Am., 75:4, 1135-1154, 1985.%% Acknowledgments: Dmitry Nicolsky, Qian Yao, Halldor Geirsson% Development history:% [2014-05-24]: fixes a bug for tilt calculation (K1) when DIP=90.% Detected by Halldor Geirsson.% [2012-11-08]: solves partially mathematical singularities in% specific cases like DIP=90, STRIKE=0, and fault reaching surface.% Detected by Qian Yao.% [2012-08-29]: allows vectorization of RAKE, SLIP and OPEN.% [2011-03-08]: help review.% [2011-03-06]: new optional argument to plot fault geometry with% output arguments, and bug correction for the fault centroid position% (in calculation and plot).% [2010-11-29]: change coordinates and depth to fault centroid% (instead of middle top edge).% [2010-09-24]: bugs correction in the syntax of I1, K2 and uyy_tf% functions, affecting some components. Detected by Dmitry Nicolsky.%% Copyright (c) 1997-2012, Franois Beauducel, covered by BSD License.% All rights reserved.%% Redistribution and use in source and binary forms, with or without% modification, are permitted provided that the following conditions are% met:%% * Redistributions of source code must retain the above copyright% notice, this list of conditions and the following disclaimer.% * Redistributions in binary form must reproduce the above copyright% notice, this list of conditions and the following disclaimer in% the documentation and/or other materials provided with the distribution%% THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"% AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE% IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE% ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE% LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR% CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF% SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS% INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN% CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)% ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE% POSSIBILITY OF SUCH DAMAGE.if nargin < 10error('Not enough input arguments.')endif nargin > 12error('Too many input arguments.')endif any(~cellfun(@isnumeric,varargin(1:10)))error('Input arguments E,N,DEPTH,STRIKE,DIP,LENGTH,WIDTH,RAKE,SLIP,OPEN must be numeric.')endif ~isscalar(varargin{5})error('DIP argument must be scalar.')end% Default values for optional input argumentsplotflag = 0; % no plotnu = 0.25; % isotropic Poisson's ratio% Assigns input argumentse = varargin{1};n = varargin{2};depth = varargin{3};strike = varargin{4}*pi/180; % converting STRIKE in radiandip = varargin{5}*pi/180; % converting DIP in radian ('delta' in Okada's equations)L = varargin{6};W = varargin{7};rake = varargin{8}*pi/180; % converting RAKE in radianslip = varargin{9};U3 = varargin{10};switch nargincase 11if isnumeric(varargin{11})nu = varargin{11};elsemakeplot = varargin{11};endcase 12makeplot = varargin{12};endif exist('makeplot','var')if strcmp(makeplot,'plot')plotflag = 1;elseerror('Unknown last argument.')endendif plotflag & any([numel(depth),numel(strike),numel(L),numel(W),numel(rake),numel(slip),numel(U3)]>1)warning('Cannot make plot with fault geometry parameters other than scalars.')plotflag = 0;end% Defines dislocation in the fault plane systemU1 = cos(rake).*slip;U2 = sin(rake).*slip;% Converts fault coordinates (E,N,DEPTH) relative to centroid% into Okada's reference system (X,Y,D)d = depth + sin(dip).*W/2; % d is fault's top edgeec = e + cos(strike).*cos(dip).*W/2;nc = n - sin(strike).*cos(dip).*W/2;x = cos(strike).*nc + sin(strike).*ec + L/2;y = sin(strike).*nc - cos(strike).*ec + cos(dip).*W;% Variable substitution (independent from xi and eta)p = y.*cos(dip) + d.*sin(dip);q = y.*sin(dip) - d.*cos(dip);% Displacementsif any(nargout==[3, 5, 7, 9])ux = -U1/(2*pi) .* chinnery(@ux_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@ux_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@ux_tf,x,p,L,W,q,dip,nu); ... % tensile faultuy = -U1/(2*pi) .* chinnery(@uy_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uy_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uy_tf,x,p,L,W,q,dip,nu); ... % tensile faultuz = -U1/(2*pi) .* chinnery(@uz_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uz_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uz_tf,x,p,L,W,q,dip,nu); ... % tensile fault% Rotation from Okada's axes to geographicue = sin(strike).*ux - cos(strike).*uy;un = cos(strike).*ux + sin(strike).*uy;end% Tiltif any(nargout==[2, 5, 6, 9])uzx = -U1/(2*pi) .* chinnery(@uzx_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uzx_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uzx_tf,x,p,L,W,q,dip,nu); ... % tensile faultuzy = -U1/(2*pi) .* chinnery(@uzy_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uzy_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uzy_tf,x,p,L,W,q,dip,nu); ... % tensile fault% Rotation from Okada's axes to geographicuze = -sin(strike).*uzx + cos(strike).*uzy;uzn = -cos(strike).*uzx - sin(strike).*uzy;end% Strainif any(nargout==[4, 6, 7, 9])uxx = -U1/(2*pi) .* chinnery(@uxx_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uxx_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uxx_tf,x,p,L,W,q,dip,nu); ... % tensile faultuxy = -U1/(2*pi) .* chinnery(@uxy_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uxy_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uxy_tf,x,p,L,W,q,dip,nu); ... % tensile faultuyx = -U1/(2*pi) .* chinnery(@uyx_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uyx_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uyx_tf,x,p,L,W,q,dip,nu); ... % tensile faultuyy = -U1/(2*pi) .* chinnery(@uyy_ss,x,p,L,W,q,dip,nu) ... % strike-slip- U2/(2*pi) .* chinnery(@uyy_ds,x,p,L,W,q,dip,nu) ... % dip-slip+ U3/(2*pi) .* chinnery(@uyy_tf,x,p,L,W,q,dip,nu); ... % tensile fault% Rotation from Okada's axes to geographicunn = cos(strike).^2*uxx + sin(2*strike).*(uxy + uyx)/2 + sin(strike).^2.*uyy;une = sin(2*strike).*(uxx - uyy)/2 + sin(strike).^2.*uyx - cos(strike).^2.*uxy;uen = sin(2*strike).*(uxx - uyy)/2 - cos(strike).^2.*uyx + sin(strike).^2.*uxy;uee = sin(strike).^2*uxx - sin(2*strike).*(uyx + uxy)/2 + cos(strike).^2.*uyy;end% Assigns output argumentsswitch nargoutcase 2varargout = {uze, uzn};case 3varargout = {ue, un, uz};case 4varargout = {unn, une, uen, uee};case 5varargout = {ue, un, uz, uze, uzn};case 6varargout = {uze, ezn, unn, une, uen, uee};case 7varargout = {ue, un, uz, unn, une, uen, uee};case 9varargout = {ue, un, uz, uze, uzn, unn, une, uen, uee};case 0plotflag = 1;otherwisedisp('Unvalid number of output arguments.')end% no output argument: plots geometry of the fault and dislocationif plotflagfigureplot(e,n,'.r','MarkerSize',.1)alpha = pi/2 - strike;x_fault = L/2*cos(alpha)*[-1,1,1,-1] + sin(alpha)*cos(dip)*W/2*[-1,-1,1,1];y_fault = L/2*sin(alpha)*[-1,1,1,-1] + cos(alpha)*cos(dip)*W/2*[1,1,-1,-1];z_fault = -d + sin(dip)*W*[1,1,0,0];ddx = U1*cos(alpha) - U2*sin(alpha)*cos(dip) + U3*sin(alpha)*sin(dip);ddy = U1*sin(alpha) + U2*cos(alpha)*cos(dip) - U3*cos(alpha)*sin(dip);ddz = U2*sin(dip) + U3*cos(dip);patch(x_fault,y_fault,z_fault,.3*[1,1,1],'EdgeColor','k','LineWidth',2)patch(x_fault+ddx/2,y_fault+ddy/2,z_fault+ddz/2,.6*[1,1,1], ...'EdgeColor','k','LineWidth',1,'FaceAlpha',.5)patch(x_fault-ddx/2,y_fault-ddy/2,z_fault-ddz/2,.6*[1,1,1], ...'EdgeColor','k','LineWidth',1,'FaceAlpha',.5)xlabel('East'); ylabel('North'); zlabel('Vertical')view(3); grid on; axis equal; rotate3dend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Notes for I... and K... subfunctions:%% 1. original formulas use Lame's parameters as mu/(mu+lambda) which% depends only on the Poisson's ratio = 1 - 2*nu% 2. tests for cos(dip) == 0 are made with "cos(dip) > eps"% because cos(90*pi/180) is not zero but = 6.1232e-17 (!)% NOTE: don't use cosd and sind because of incompatibility% with Matlab v6 and earlier...% =================================================================% Chinnery's notation [equation (24) p. 1143]% -----------------------------------------------------------------function u=chinnery(f,x,p,L,W,q,dip,nu)u = feval(f,x,p,q,dip,nu) ...- feval(f,x,p-W,q,dip,nu) ...- feval(f,x-L,p,q,dip,nu) ...+ feval(f,x-L,p-W,q,dip,nu);% =================================================================% Displacement subfunctions% strike-slip displacement subfunctions [equation (25) p. 1144]% -----------------------------------------------------------------function u=ux_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = xi.*q./(R.*(R + eta)) ...+ I1(xi,eta,q,dip,nu,R).*sin(dip);k = find(q~=0);u(k) = u(k) + atan(xi(k).*eta(k)./(q(k).*R(k)));% -----------------------------------------------------------------function u=uy_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = (eta.*cos(dip) + q.*sin(dip)).*q./(R.*(R + eta)) ...+ q.*cos(dip)./(R + eta) ...+ I2(eta,q,dip,nu,R).*sin(dip);% -----------------------------------------------------------------function u=uz_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);u = (eta.*sin(dip) - q.*cos(dip)).*q./(R.*(R + eta)) ...+ q.*sin(dip)./(R + eta) ...+ I4(db,eta,q,dip,nu,R).*sin(dip);% dip-slip displacement subfunctions [equation (26) p. 1144]% -----------------------------------------------------------------function u=ux_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = q./R ...- I3(eta,q,dip,nu,R).*sin(dip).*cos(dip);% -----------------------------------------------------------------function u=uy_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = (eta.*cos(dip) + q.*sin(dip)).*q./(R.*(R + xi)) ...- I1(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);k = find(q~=0);u(k) = u(k) + cos(dip).*atan(xi(k).*eta(k)./(q(k).*R(k)));% -----------------------------------------------------------------function u=uz_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);u = db.*q./(R.*(R + xi)) ...- I5(xi,eta,q,dip,nu,R,db).*sin(dip).*cos(dip);k = find(q~=0);u(k) = u(k) + sin(dip).*atan(xi(k).*eta(k)./(q(k).*R(k)));% tensile fault displacement subfunctions [equation (27) p. 1144]% -----------------------------------------------------------------function u=ux_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = q.^2 ./(R.*(R + eta)) ...- I3(eta,q,dip,nu,R).*sin(dip).^2;% -----------------------------------------------------------------function u=uy_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = -(eta.*sin(dip) - q.*cos(dip)).*q./(R.*(R + xi)) ...- sin(dip).*xi.*q./(R.*(R + eta)) ...- I1(xi,eta,q,dip,nu,R).*sin(dip).^2;k = find(q~=0);u(k) = u(k) + sin(dip).*atan(xi(k).*eta(k)./(q(k).*R(k)));% -----------------------------------------------------------------function u=uz_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);u = (eta.*cos(dip) + q.*sin(dip)).*q./(R.*(R + xi)) ...+ cos(dip).*xi.*q./(R.*(R + eta)) ...- I5(xi,eta,q,dip,nu,R,db).*sin(dip).^2;k = find(q~=0);u(k) = u(k) - cos(dip).*atan(xi(k).*eta(k)./(q(k).*R(k)));% I... displacement subfunctions [equations (28) (29) p. 1144-1145]% -----------------------------------------------------------------function I=I1(xi,eta,q,dip,nu,R)db = eta.*sin(dip) - q.*cos(dip);if cos(dip) > epsI = (1 - 2*nu) * (-xi./(cos(dip).*(R + db))) ...- sin(dip)./cos(dip).*I5(xi,eta,q,dip,nu,R,db);elseI = -(1 - 2*nu)/2 * xi.*q./(R + db).^2;end% -----------------------------------------------------------------function I=I2(eta,q,dip,nu,R)I = (1 - 2*nu) * (-log(R + eta)) - I3(eta,q,dip,nu,R);% -----------------------------------------------------------------function I=I3(eta,q,dip,nu,R)yb = eta.*cos(dip) + q.*sin(dip);db = eta.*sin(dip) - q.*cos(dip);if cos(dip) > epsI = (1 - 2*nu) * (yb./(cos(dip)*(R + db)) - log(R + eta)) ...+ sin(dip)./cos(dip) * I4(db,eta,q,dip,nu,R);elseI = (1 - 2*nu)/2 * (eta./(R + db) + yb.*q./(R + db).^2 - log(R + eta));end% -----------------------------------------------------------------function I=I4(db,eta,q,dip,nu,R)if cos(dip) > epsI = (1 - 2*nu) * 1./cos(dip) * (log(R + db) - sin(dip).*log(R + eta));elseI = -(1 - 2*nu) * q./(R + db);end% -----------------------------------------------------------------function I=I5(xi,eta,q,dip,nu,R,db)X = sqrt(xi.^2 + q.^2);if cos(dip) > epsI = (1 - 2*nu) * 2./cos(dip) ....* atan((eta.*(X + q.*cos(dip)) + X.*(R + X).*sin(dip)) ..../(xi.*(R + X).*cos(dip)));I(xi==0) = 0;elseI = -(1 - 2*nu) * xi.*sin(dip)./(R + db);end% =================================================================% Tilt subfunctions% strike-slip tilt subfunctions [equation (37) p. 1147]% -----------------------------------------------------------------function u=uzx_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = -xi.*q.^2.*A(eta,R).*cos(dip) ...+ ((xi.*q)./R.^3 - K1(xi,eta,q,dip,nu,R)).*sin(dip);% -----------------------------------------------------------------function u=uzy_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);yb = eta.*cos(dip) + q.*sin(dip);u = (db.*q./R.^3).*cos(dip) ...+ (xi.^2.*q.*A(eta,R).*cos(dip) - sin(dip)./R + yb.*q./R.^3 ...- K2(xi,eta,q,dip,nu,R)).*sin(dip);% dip-slip tilt subfunctions [equation (38) p. 1147]% -----------------------------------------------------------------function u=uzx_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);u = db.*q./R.^3 ...+ q.*sin(dip)./(R.*(R + eta)) ...+ K3(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);% -----------------------------------------------------------------function u=uzy_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);yb = eta.*cos(dip) + q.*sin(dip);u = yb.*db.*q.*A(xi,R) ...- (2*db./(R.*(R + xi)) + xi.*sin(dip)./(R.*(R + eta))).*sin(dip) ...+ K1(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);% tensile fault tilt subfunctions [equation (39) p. 1147]% -----------------------------------------------------------------function u=uzx_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = q.^2./R.^3.*sin(dip) ...- q.^3.*A(eta,R).*cos(dip) ...+ K3(xi,eta,q,dip,nu,R).*sin(dip).^2;% -----------------------------------------------------------------function u=uzy_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);yb = eta.*cos(dip) + q.*sin(dip);u = (yb.*sin(dip) + db.*cos(dip)).*q.^2.*A(xi,R) ...+ xi.*q.^2.*A(eta,R).*sin(dip).*cos(dip) ...- (2*q./(R.*(R + xi)) - K1(xi,eta,q,dip,nu,R)).*sin(dip).^2;% -----------------------------------------------------------------function a=A(x,R)a = (2*R + x)./(R.^3.*(R + x).^2);% K... tilt subfunctions [equations (40) (41) p. 1148]% -----------------------------------------------------------------function K=K1(xi,eta,q,dip,nu,R)db = eta.*sin(dip) - q.*cos(dip);if cos(dip) > epsK = (1 - 2*nu) * xi./cos(dip) .* (1./(R.*(R + db)) - sin(dip)./(R.*(R + eta)));elseK = (1 - 2*nu) * xi.*q./(R.*(R + db).^2);end% -----------------------------------------------------------------function K=K2(xi,eta,q,dip,nu,R)K = (1 - 2*nu) * (-sin(dip)./R + q.*cos(dip)./(R.*(R + eta))) ...- K3(xi,eta,q,dip,nu,R);% -----------------------------------------------------------------function K=K3(xi,eta,q,dip,nu,R)db = eta.*sin(dip) - q.*cos(dip);yb = eta.*cos(dip) + q.*sin(dip);if cos(dip) > epsK = (1 - 2*nu) * 1./cos(dip) .* (q./(R.*(R + eta)) - yb./(R.*(R + db)));elseK = (1 - 2*nu) * sin(dip)./(R + db) .* (xi.^2./(R.*(R + db)) - 1);end% =================================================================% Strain subfunctions% strike-slip strain subfunctions [equation (31) p. 1145]% -----------------------------------------------------------------function u=uxx_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = xi.^2.*q.*A(eta,R) ...- J1(xi,eta,q,dip,nu,R).*sin(dip);% -----------------------------------------------------------------function u=uxy_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);u = xi.^3.*db./(R.^3.*(eta.^2 + q.^2)) ...- (xi.^3.*A(eta,R) + J2(xi,eta,q,dip,nu,R)).*sin(dip);% -----------------------------------------------------------------function u=uyx_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = xi.*q./R.^3.*cos(dip) ...+ (xi.*q.^2.*A(eta,R) - J2(xi,eta,q,dip,nu,R)).*sin(dip);% -----------------------------------------------------------------function u=uyy_ss(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);yb = eta.*cos(dip) + q.*sin(dip);u = yb.*q./R.^3.*cos(dip) ...+ (q.^3.*A(eta,R).*sin(dip) - 2*q.*sin(dip)./(R.*(R + eta)) ...- (xi.^2 + eta.^2)./R.^3.*cos(dip) - J4(xi,eta,q,dip,nu,R)).*sin(dip);% dip-slip strain subfunctions [equation (32) p. 1146]% -----------------------------------------------------------------function u=uxx_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = xi.*q./R.^3 ...+ J3(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);% -----------------------------------------------------------------function u=uxy_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);yb = eta.*cos(dip) + q.*sin(dip);u = yb.*q./R.^3 ...- sin(dip)./R ...+ J1(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);% -----------------------------------------------------------------function u=uyx_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);yb = eta.*cos(dip) + q.*sin(dip);u = yb.*q./R.^3 ...+ q.*cos(dip)./(R.*(R + eta)) ...+ J1(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);% -----------------------------------------------------------------function u=uyy_ds(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);yb = eta.*cos(dip) + q.*sin(dip);u = yb.^2.*q.*A(xi,R) ...- (2*yb./(R.*(R + xi)) + xi.*cos(dip)./(R.*(R + eta))).*sin(dip) ...+ J2(xi,eta,q,dip,nu,R).*sin(dip).*cos(dip);% tensile fault strain subfunctions [equation (33) p. 1146]% -----------------------------------------------------------------function u=uxx_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = xi.*q.^2.*A(eta,R) ...+ J3(xi,eta,q,dip,nu,R).*sin(dip).^2;% -----------------------------------------------------------------function u=uxy_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);u = -db.*q./R.^3 ...- xi.^2.*q.*A(eta,R).*sin(dip) ...+ J1(xi,eta,q,dip,nu,R).*sin(dip).^2;% -----------------------------------------------------------------function u=uyx_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);u = q.^2./R.^3.*cos(dip) ...+ q.^3.*A(eta,R).*sin(dip) ...+ J1(xi,eta,q,dip,nu,R).*sin(dip).^2;% -----------------------------------------------------------------function u=uyy_tf(xi,eta,q,dip,nu)R = sqrt(xi.^2 + eta.^2 + q.^2);db = eta.*sin(dip) - q.*cos(dip);yb = eta.*cos(dip) + q.*sin(dip);u = (yb.*cos(dip) - db.*sin(dip)).*q.^2.*A(xi,R) ...- q.*sin(2*dip)./(R.*(R + xi)) ...- (xi.*q.^2.*A(eta,R) - J2(xi,eta,q,dip,nu,R)).*sin(dip).^2;% J... tensile fault subfunctions [equations (34) (35) p. 1146-1147]% -----------------------------------------------------------------function J=J1(xi,eta,q,dip,nu,R)db = eta.*sin(dip) - q.*cos(dip);if cos(dip) > epsJ = (1 - 2*nu) * 1./cos(dip) * (xi.^2./(R.*(R + db).^2) - 1./(R + db)) ...- sin(dip)./cos(dip)*K3(xi,eta,q,dip,nu,R);elseJ = (1 - 2*nu)/2 * q./(R + db).^2 .* (2*xi.^2./(R.*(R + db)) - 1);end% -----------------------------------------------------------------function J=J2(xi,eta,q,dip,nu,R)db = eta.*sin(dip) - q.*cos(dip);yb = eta.*cos(dip) + q.*sin(dip);if cos(dip) > epsJ = (1 - 2*nu) * 1./cos(dip) * xi.*yb./(R.*(R + db).^2) ...- sin(dip)./cos(dip)*K1(xi,eta,q,dip,nu,R);elseJ = (1 - 2*nu)/2 * xi.*sin(dip)./(R + db).^2 .* (2*q.^2./(R.*(R + db)) - 1);end% -----------------------------------------------------------------function J=J3(xi,eta,q,dip,nu,R)J = (1 - 2*nu) * -xi./(R.*(R + eta)) ...- J2(xi,eta,q,dip,nu,R);% -----------------------------------------------------------------function J=J4(xi,eta,q,dip,nu,R)J = (1 - 2*nu) * (-cos(dip)./R - q.*sin(dip)./(R.*(R + eta))) ...- J1(xi,eta,q,dip,nu,R);
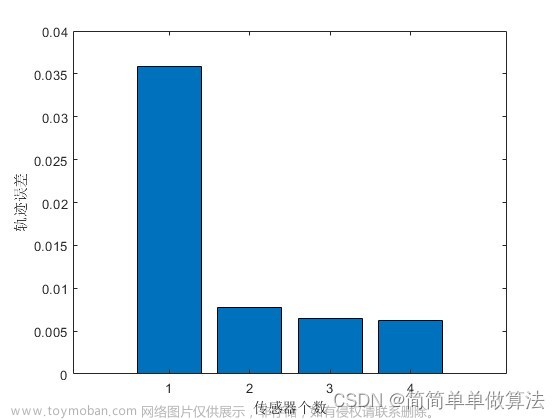
⛳️ 运行结果


🔗 参考文献
🎈 部分理论引用网络文献,若有侵权联系博主删除
🎁 关注我领取海量matlab电子书和数学建模资料
👇 私信完整代码和数据获取及论文数模仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱船配载优化、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化
2 机器学习和深度学习方面
2.1 bp时序、回归预测和分类
2.2 ENS声神经网络时序、回归预测和分类
2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类
2.4 CNN/TCN卷积神经网络系列时序、回归预测和分类
2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类
2.7 ELMAN递归神经网络时序、回归\预测和分类文章来源:https://www.toymoban.com/news/detail-857555.html
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类
2.9 RBF径向基神经网络时序、回归预测和分类文章来源地址https://www.toymoban.com/news/detail-857555.html
2.10 DBN深度置信网络时序、回归预测和分类
2.11 FNN模糊神经网络时序、回归预测
2.12 RF随机森林时序、回归预测和分类
2.13 BLS宽度学习时序、回归预测和分类
2.14 PNN脉冲神经网络分类
2.15 模糊小波神经网络预测和分类
2.16 时序、回归预测和分类
2.17 时序、回归预测预测和分类
2.18 XGBOOST集成学习时序、回归预测预测和分类
方向涵盖风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、用电量预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、 充电车辆路径规划(EVRP)、 双层车辆路径规划(2E-VRP)、 油电混合车辆路径规划、 船舶航迹规划、 全路径规划规划、 仓储巡逻
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化、车辆协同无人机路径规划
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置、有序充电
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长 金属腐蚀
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合
到了这里,关于基于卡尔曼滤波检测GNSS 数据中的智能手机位移附matlab代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!