算法系列--动态规划--背包问题(3)--完全背包介绍

这篇具有很好参考价值的文章主要介绍了算法系列--动态规划--背包问题(3)--完全背包介绍。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

💕"Su7"💕
作者：Lvzi
文章主要内容：算法系列–动态规划–背包问题(3)–完全背包介绍

大家好,今天为大家带来的是算法系列--动态规划--背包问题(3)--完全背包介绍

一.完全背包问题

链接:
完全背包

动态规划完全背包问题,算法,动态规划
可以发现完全背包问题和01背包问题还是特比相似的

分析:

完全背包问题是01背包问题的推广,是以01背包问题为基础,两种问题的状态表示是相同的

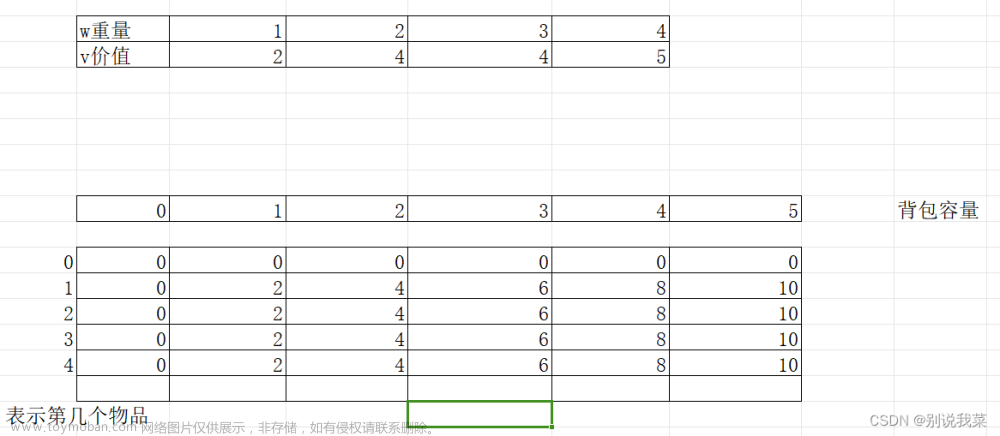
dp[i][j]:在[1,i]所有物品中,在不超过体积j的前提下,可以实现的最大价值

分析状态转移方程时也是以最后一个位置的状态去划分,分为选/不选nums[i],此处就体现出完全背包问题和01背包问题最大的差别,01背包问题如果选择nums[i],选择的物品的数量只能是1(+w[i]),但是完全背包问题如果选择nums[i],可以选择的数量是任意多个(+n * w[i]),此时的状态是任意多个,这样的状态我们在正则表达式匹配那道问题中已经遇到过,解决思路就是利用数学规律,将任意多个状态使用简单的几个状态表示,具体操作是观察所有状态中不变的量,大胆假设,小心求证!!!

以下是状态转移方程的推导:
动态规划完全背包问题,算法,动态规划

动态规划完全背包问题,算法,动态规划

dp[i][j] = Max(dp[i-1][j],dp[i][j - nums[i]] + w[i])

初始化

根据状态表示分析出不需要初始化

返回值:

dp[n][V]

代码:

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        // 1.解决第一问
        Scanner in = new Scanner(System.in);
        int n = in.nextInt(), V = in.nextInt();// 获取物品数目和体积

        int[] v = new int[n + 1], w = new int[n + 1];
        for(int i = 1; i <= n; i++) {
            v[i] = in.nextInt();// 物品体积
            w[i] = in.nextInt();// 物品价值
        }

        int[][] dp = new int[n + 1][V + 1];
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= V; j++) {
                dp[i][j] = dp[i-1][j];
                if(j - v[i] >= 0)
                    dp[i][j] = Math.max(dp[i][j],dp[i][j - v[i]] + w[i]);
            }
        }

        System.out.println(dp[n][V]);

        // 1.解决第二问
        dp = new int[n + 1][ V + 1];// 好的代码风格?
        for(int j = 1; j <= V; j++) dp[0][j] = -1;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= V; j++) {
                dp[i][j] = dp[i - 1][j];
                if(j - v[i] >= 0 && dp[i][j - v[i]] != -1)
                    dp[i][j] = Math.max(dp[i][j],dp[i][j - v[i]] + w[i]);
            }
        }
        System.out.println(dp[n][V] == -1 ? 0 : dp[n][V]);
    }
}

空间优化:
同样的在完全背包问题中也可以进行空间优化(想想01背包问题中的空间优化,通过明确遍历顺序,只是用一个简单的线性数组就可以完成填表)

01背包问题的空间优化最需要注意的就是遍历顺序的改变,在01背包问题中,为了在填表的时候需要使用的数据不被覆盖掉,需要从右往左遍历,但是在完全背包问题中,需要从左往右遍历
动态规划完全背包问题,算法,动态规划

空间优化后的代码:

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        // 1.解决第一问
        Scanner in = new Scanner(System.in);
        int n = in.nextInt(), V = in.nextInt();// 获取物品数目和体积

        int[] v = new int[n + 1], w = new int[n + 1];
        for(int i = 1; i <= n; i++) {
            v[i] = in.nextInt();// 物品体积
            w[i] = in.nextInt();// 物品价值
        }

        int[] dp = new int[V + 1];
        for(int i = 1; i <= n; i++)
            for(int j = v[i]; j <= V; j++)
                dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);

        System.out.println(dp[V]);

        // 2.解决第二问
        dp = new int[ V + 1];// 好的代码风格?
        for(int j = 1; j <= V; j++) dp[j] = -1;
        for(int i = 1; i <= n; i++)
            for(int j = v[i]; j <= V; j++)
                if(dp[j - v[i]] != -1)
                    dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);
            
        System.out.println(dp[V] == -1 ? 0 : dp[V]);
    }
}