}
else
{
Result[j] = max(preResult[j],preResult[j-p[i]]+G[i]);
}
}
for (int i = 0; i < w; i++)
{
cout << Result[i]<<" ";
preResult[i] = Result[i];//计算完一行计算下一行 结果变成上一行的结果
//cout << preResult[i];
}
cout << endl;
}
return Result[w-1];
}
int main()
{
int p[5] = { 5,5,3,4,3 };
int Result;
int n = 5;
int w = 10;
int G[5] ={400,500,200,300,350};
Result =getMaxValue(p, n, w, G);
cout << Result<<endl;
system(“pause”);
}
输出(1)

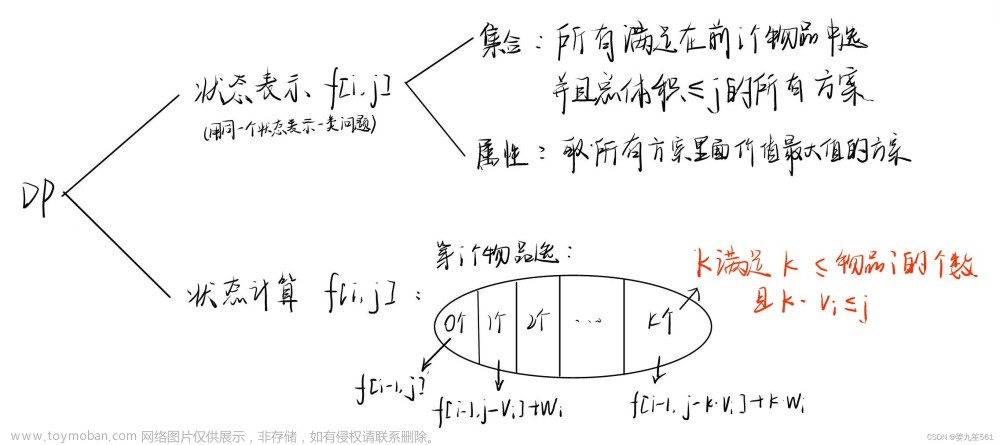
问题描述(2)0-1背包问题
=============================================================================
一个小偷来出来活动了, 拿了一个背包, 最多可以装50斤的东西的小袋子。 他眼睛一亮, 发现了三件宝贝a, b, c. 其中a重10斤, 价值60元; b重20斤, 价值100元; c重30斤, 价值120元。 问: 在背包允许的范围内, 小偷最多能偷到多少钱?
代码(2)
#include
using namespace std;
#define N 3 // N件宝贝
#define V 5 // V是背包的总capacity
int main()
{
int value[N + 1] = {0, 60, 100, 120}; // 钱啊
int weight[N + 1] = {0, 1, 2, 3}; // 重量
int f[N + 1][V + 1] = {0}; // f[i][j]表示在背包容量为j的情况下, 前i件宝贝的最大价值
int i = 1;
int j = 1;
for(i = 1; i <= N; i++)
{
for(j = 1; j <= V; j++)
{
// 递推关系式出炉
if(j < weight[i])
{
f[i][j] = f[i - 1][j];
}
else
{
int x = f[i - 1][j];
int y = f[i - 1][j - weight[i]] + value[i];
f[i][j] = x < y ? y : x;
}
}
}
for(i = N; i >= 1; i–)
{
for(j = 1; j <= V; j++)
{
printf("%4d ", f[i][j]);
}
cout << endl;
}
return 0;
}
输出(2)

0-1背包 简化
=======================================================================
物品个数n=5,物品重量w[5]={2,2,6,5,4},物品价值v[5]={6,3,5,4,6}, 背包的最大容量为10,求价值最大化。
代码:
#include
using namespace std;
#define N 5 // N件宝贝
#define V 10 // C是背包的总capacity
int main()
{
int value[N + 1] = {0, 6, 3, 5, 4, 6}; // 钱啊
int weight[N + 1] = {0, 2, 2, 6, 5, 4}; // 重量
int f[N + 1][V + 1] = {0}; // f[i][j]表示在背包容量为j的情况下, 前i件宝贝的最大价值
int i = 1;
int j = 1;
for(i = 1; i <= N; i++)
{
for(j = 1; j <= V; j++)
{
// 递推关系式出炉
if(j < weight[i])
{
f[i][j] = f[i - 1][j];
}
else
{
int x = f[i - 1][j];
int y = f[i - 1][j - weight[i]] + value[i];
f[i][j] = x < y ? y : x;
}
}
}
for(i = N; i >= 1; i–)
自我介绍一下,小编13年上海交大毕业,曾经在小公司待过,也去过华为、OPPO等大厂,18年进入阿里一直到现在。
深知大多数前端工程师,想要提升技能,往往是自己摸索成长或者是报班学习,但对于培训机构动则几千的学费,着实压力不小。自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞不前!
因此收集整理了一份《2024年Web前端开发全套学习资料》,初衷也很简单,就是希望能够帮助到想自学提升又不知道该从何学起的朋友,同时减轻大家的负担。


既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,基本涵盖了95%以上前端开发知识点,真正体系化!

由于文件比较大,这里只是将部分目录截图出来,每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频,并且会持续更新!
如果你觉得这些内容对你有帮助,可以扫码获取!!(备注:前端)

最后
整理面试题,不是让大家去只刷面试题,而是熟悉目前实际面试中常见的考察方式和知识点,做到心中有数,也可以用来自查及完善知识体系。
《前端基础面试题》,《前端校招面试题精编解析大全》,《前端面试题宝典》,《前端面试题:常用算法》PDF完整版点击这里领取



理面试题,不是让大家去只刷面试题,而是熟悉目前实际面试中常见的考察方式和知识点,做到心中有数,也可以用来自查及完善知识体系。
《前端基础面试题》,《前端校招面试题精编解析大全》,《前端面试题宝典》,《前端面试题:常用算法》PDF完整版点击这里领取
[外链图片转存中…(img-4TxTx69L-1712559553309)]
[外链图片转存中…(img-D7Jeyibc-1712559553310)]文章来源:https://www.toymoban.com/news/detail-858196.html
[外链图片转存中…(img-7Y2lvvDK-1712559553310)]文章来源地址https://www.toymoban.com/news/detail-858196.html
到了这里,关于【动态规划之“0-1背包问题”----国王和金矿问题----C++实现】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!