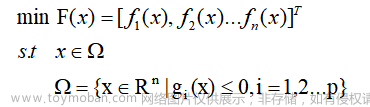使用 Python库DEAP的多目标优化示例-Toy模板网

这篇具有很好参考价值的文章主要介绍了使用 Python库DEAP的多目标优化示例。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、说明

在优化领域，困难往往不是来自为单个问题找到最佳解决方案，而是来自管理具有多个经常相互冲突的目标的复杂问题环境。这就是多目标优化（MOO）发挥作用的地方，它提供了一个解决此类多方面问题的框架。本文探讨了 MOO 的核心及其数学基础，并提供了一个动手 Python 示例来说明这些概念。

二、了解多目标优化

多目标优化是数学建模和计算智能中的一个重要领域，专注于涉及多个目标函数同时优化的问题。这些目标通常是相互冲突的，这意味着改进一个目标可能会使另一个目标恶化。MOO 的目标不是找到单一的最优解决方案，而是确定一组最佳解决方案，同时考虑相互竞争的目标之间的权衡。

核心理念：

目标：优化过程寻求实现的不同目标。在 MOO 中，总是有两个或多个目标。
帕累托最优性：如果一个目标不能在不恶化至少一个其他目标的情况下得到改进，则解决方案是帕累托最优的。这些解决方案的集合形成了帕累托阵线。
权衡：必须在目标之间做出妥协，因为改进一个目标通常是以牺牲另一个目标为代价的。

三、多目标优化中的数学建模

3.1 多目标优化任务定义

多目标优化问题可以用数学公式表述如下：
给出一组函数： $f_1(x),f_2(x),f_3(x)...f_k(x)$
服从条件： $\in X$
$f_1 ,f_2 ,f_3 ...f_k$ 是目标函数，在优化中取最大或最小。
X：表示合理化集合，盛放x的所有可能取值。
此时用python的DEAP库进行实现。首先给出一个例子：
example 1：最小化的目标函数 $f_1(x)=x^2$ ,最小化目标函数： $f_1(x)=（x-2）^2$

3.2 环境设定

安装deap命令

pip install deap

3.3 精心设计解决方案

让我们看一下代码，分解每个步骤，以了解如何使用 DEAP 实现 MOO。

第 1 步：定义问题

首先，我们需要根据 DEAP 的框架来定义我们的问题，明确我们目标的性质和我们个人的结构（解决方案）。

from deap import base, creator, tools, algorithms
import random


# Problem definition
creator.create("FitnessMin", base.Fitness, weights=(-1.0, -1.0))  # Minimize both objectives
creator.create("Individual", list, fitness=creator.FitnessMin)  # Define individual structure

步骤 2：初始化工具箱

DEAP中的工具箱是我们注册遗传操作的方法的地方，例如突变，交叉和选择，以及我们针对特定问题的配置。

toolbox = base.Toolbox()
toolbox.register("attr_float", random.uniform, -10, 10)  # Decision variable range
toolbox.register("individual", tools.initRepeat, creator.Individual,
                 toolbox.attr_float, n=1)  # Individual creation
toolbox.register("population", tools.initRepeat, list, toolbox.individual)  # Population creation

步骤 3：定义评估函数

我们的评估功能计算给定解决方案的目标。这个功能至关重要，因为它指导着进化过程。

def evaluate(individual):
    x = individual[0]
    return x**2, (x-2)**2  # The two objectives
toolbox.register("evaluate", evaluate)

第 4 步：遗传算子

我们定义了交配（交叉）、突变和选择的遗传算子。这些算子使解决方案能够向帕累托前沿演进。

toolbox.register("mate", tools.cxBlend, alpha=0.5)
toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=1, indpb=0.2)
toolbox.register("select", tools.selNSGA2)  # NSGA-II selection algorithm

第 5 步：进化算法

最后，我们实现了主要的进化循环，将我们的人口进化到帕累托前沿。

def main():
    random.seed(1)
    population = toolbox.population(n=100)  # Initial population
    NGEN = 50  # Number of generations

    # Evolutionary loop
    for gen in range(NGEN):
        offspring = algorithms.varAnd(population, toolbox, cxpb=0.5, mutpb=0.2)
        fits = toolbox.map(toolbox.evaluate, offspring)
        for fit, ind in zip(fits, offspring):
            ind.fitness.values = fit
        population = toolbox.select(offspring, k=len(population))

    return population

if __name__ == "__main__":
    pop = main()
    front = tools.emo.sortNondominated(pop, len(pop), first_front_only=True)[0]

    # Display the Pareto front
    print("Pareto Front:")
    for ind in front:
        print(ind.fitness.values)