【数学建模】钻井问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数学建模】钻井问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

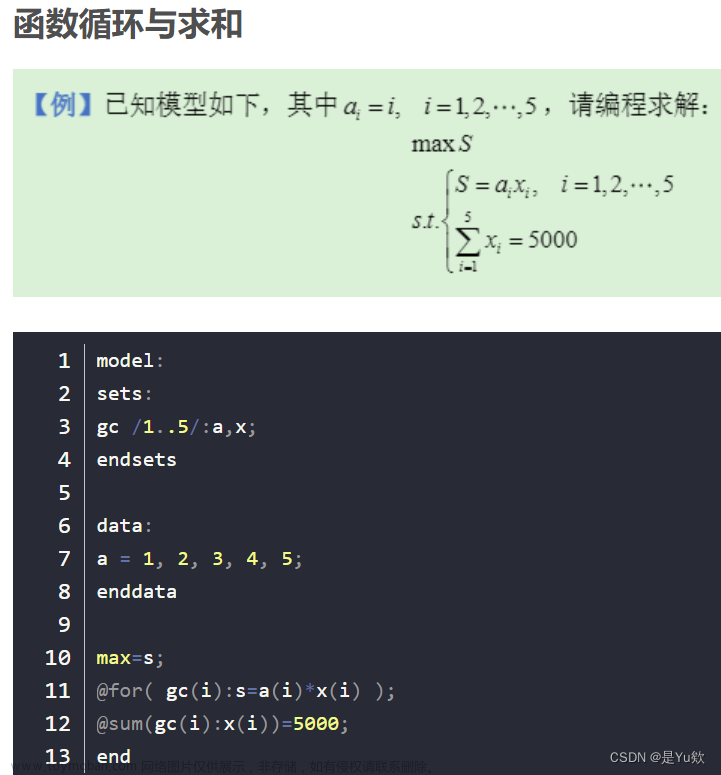
已知

12口井的坐标位置如下:
x=[0.50,1.41,3.00,3.37,3.40,4.72,4.72,5.43,7.57,8.38,8.98, 9.50];
y=[2.00,3.50,1.50,3.51,5.50,2.00,6.24,4.10,2.01,4.50,3.41,0.80];
设平面有n个点 $P_i$ (表旧井井位),其坐标为 $a_i,b_i),i=1,2,…,n$ 。新置的井位是一个正方形网格 $N$ 的所有结点。假设每个格子的边长都是 $1$ 单位。整个网格是可以在平面上任意移动的。若一个已知点 $P_i$ 距某个网格结点 $X_i$ 的距离不超过给定误差 $\epsilon$ ,则认为 $P_i$ 处的旧井井位可以利用,不必在结点处打新井。

1)假定网格的横向和纵向是固定的,并规定两点间的距离为其横向距离(横坐标之差的绝对值)及纵向距离(纵坐标之差的绝对值)的最大者,在平面上平移网格N,使可利用的旧井数尽可能大,试提供数值计算方法。

本题主要是要建立旧井可利用判断模型

首先是按照题目建立两点距离符合误差 $\epsilon$ 范围内的判断模型
若一个已知点 $P_i$ $a_i,b_i)$ 距某个网格结点 $X_i(x_i,y_i)$ 的距离不超过给定误差 $\epsilon$
$\begin{cases} |a_i-x_i| \le \epsilon \\ |b_i-y_i| \le \epsilon \end{cases}$
或者

$\max{(|a_i-x_i|,|b_i-y_i|)}\le \epsilon$

其次是网格平移模型，因为要研究的是网格平行对井的位置变化
设网格向右平移 $x$ 个单位，向上平移 $y$ 个单位;一个已知点 $P_i$ $a_i,b_i)$
;网格平移后新点位置 $P_j(a_j,b_j)$
有 $\begin{cases} a_j = a_i+x \\ b_j = b_i + y \end{cases}$

综合上述模型和要可利用的旧井数尽可能大可得模型:

$\begin{cases} ans = \max \sum_{\substack{i\in N\\1\le i\le n} }{fi} \\ \max{(|a_i+x-x_i|,|b_i + y-y_i|)f_i}\le \epsilon \end{cases}$

现在还剩下一个问题某个网格结点 $X_i(x_i,y_i)$ 是哪个网格点
这里问题就可以变成一个已知点 $P_j$ $a_j,b_j)$ 求距离其最近的网格点 $X_j(x_j,y_j)$
将一个小格子划分为四个区域观察规律可得
$\begin{cases} x_j = \lfloor a_j+0.5 \rfloor \\ y_j = \lfloor b_j+0.5 \rfloor \end{cases}$

将这个式子带入我们的模型中可得
$\begin{cases} ans = \max \sum_{\substack{i\in N\\1\le i\le n} }{fi} \\ \max{(|a_i+x-\lfloor a_i+x+0.5 \rfloor|,|b_i + y-\lfloor b_i+y+0.5 \rfloor|)f_i}\le \epsilon \end{cases}$

给出12口井的坐标， ϵ = 0.05 \epsilon = 0.05 ϵ=0.05 , 按照问题一的要求求解

按照问题一给的模型，进行调整
$\begin{cases} ans = \max \sum_{\substack{i\in N\\1\le i\le n} }{fi} \\ \max{(|x_i+x-\lfloor x_i+x+0.5 \rfloor|,|y_i + y-\lfloor y_i+y+0.5 \rfloor|)f_i}\le 0.05 \end{cases}$

LINGO求解

sets:
	aa/1..12/:a,b,f;
endsets
data:
	a=0.50,1.41,3.00,3.37,3.40,4.72,4.72,5.43,7.57,8.38,8.98,9.50;
	b=2.00,3.50,1.50,3.51,5.50,2.00,6.24,4.10,2.01,4.50,3.41,0.80;
enddata
max = @sum(aa(i):f(i));
@for(aa(i):@bin(f(i)));
@for(aa(i):@smax(@abs(a(i)+x1-@floor(a(i)+x1+0.5)),@abs(b(i)+y1-@floor(b(i)+y1+0.5)))*f(i)<=0.05);
x1<1;
y1<1;

or
$\begin{cases} ans = \max \sum_{\substack{i\in N\\1\le i\le n} }{fi} \\ |x_i+x-\lfloor x_i+x+0.5 \rfloor|f_i\le 0.05\\|y_i + y-\lfloor y_i+y+0.5 \rfloor|f_i\le 0.05 \end{cases}$

sets:
	aa/1..12/:a,b,f;
endsets
data:
	a=0.50,1.41,3.00,3.37,3.40,4.72,4.72,5.43,7.57,8.38,8.98,9.50;
	b=2.00,3.50,1.50,3.51,5.50,2.00,6.24,4.10,2.01,4.50,3.41,0.80;
enddata
max = @sum(aa(i):f(i));
@for(aa(i):@bin(f(i)));
@for(aa(i):@abs(a(i)+x1-@floor(a(i)+x1+0.5))*f(i)<=0.05);
@for(aa(i):@abs(b(i)+y1-@floor(b(i)+y1+0.5))*f(i)<=0.05);
x1<1;
y1<1;

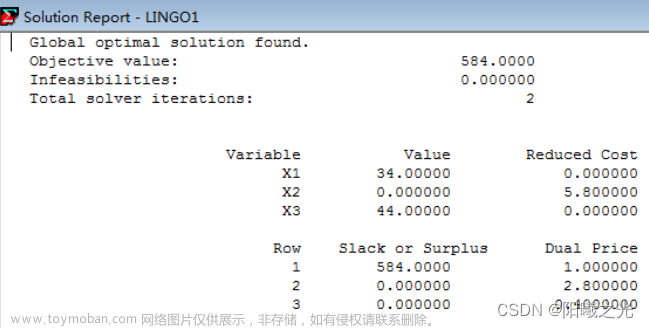
答案如下文章来源地址https://www.toymoban.com/news/detail-858586.html

  Objective value:                              4.000000
  Objective bound:                              4.000000

 						  F( 1)        0.000000           -1.000000
                          F( 2)        1.000000            0.000000
                          F( 3)        0.000000           -1.000000
                          F( 4)        1.000000           -1.000000
                          F( 5)        1.000000            0.000000
                          F( 6)        0.000000           -1.000000
                          F( 7)        0.000000           -1.000000
                          F( 8)        0.000000           -1.000000
                          F( 9)        0.000000           -1.000000
                         F( 10)        1.000000            0.000000
                         F( 11)        0.000000           -1.000000
                         F( 12)        0.000000           -1.000000