题目:
输入一个包括 '(' 和 ')' 的字符串string ,判断字符串是否有效。要求设计算法实现检查字符串是否有效,有效的字符串需满足以下条件:
A. 左括号必须用相同类型的右括号闭合。
B. 左括号必须以正确的顺序闭合。
C. 每个右括号都有一个对应的相同类型的左括号。
题目分析:
该题需要满足三个条件,左括号类型,数量,顺序都得一致,所以选择使用顺序栈结构来实现。
主要思路为遍历两次字符串。第一次遍历时,将遇到的左括号依次存入顺序栈中;第二次遍历时,每当遇到右括号时,便执行弹栈操作,并将弹栈出的元素与右括号类型进行对比。若类型一致,则继续遍历;若类型不一致,则将此时的栈顶元素下标加一且终止遍历,代表该字符串无效。
最后通过判断顺序栈中栈顶元素下标是否为-1,即顺序栈中是否还有元素,来判定字符串是否有效。
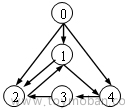
原理图示:

代码实现:
/*********************************************************************
*
* name : SeqStack_JudgString
* function : 根据用户输入的字符串中的括号个数与匹配度进行判断字符串的
正确性
* argument :
* @Manager :顺序栈的地址
*
* retval : 调用成功返回新的栈地址
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
void SeqStack_JudgString( DataType_t *str)
{
//创建顺序栈
SeqStack_t *SequenceStack = SeqStack_Create(sizeof(str));
//计算得到的字符串长度
int n = strlen(str);
//遍历得到的字符串,将字符串中各中类型的左括号按先后顺序放入顺序栈中
for (int i = 0; i < n;i++)
{
if(str[i] == '(')
SeqStack_Push(SequenceStack, str[i]);
else if(str[i] == '[')
SeqStack_Push(SequenceStack, str[i]);
else if(str[i] == '{')
SeqStack_Push(SequenceStack, str[i]);
}
//再次对字符串遍历,找到对应的右括号,并且判断类型是否相符合
for (int i = 0; i < n; i++)
{
if(str[i] == ')')
{
DataType_t temp = SeqStack_Pop(SequenceStack);
if('('== temp) //弹栈出的元素是相同类型的左括号时,继续遍历
continue;
else
{
SequenceStack->Top++;
break;
}
}
else if(str[i] == ']')
{
DataType_t temp1 = SeqStack_Pop(SequenceStack);
if('[' == temp1)
continue;
else
{
SequenceStack->Top++;
break;
}
}
else if(str[i] == '}')
{
DataType_t temp2 = SeqStack_Pop(SequenceStack);
if('{'== temp2)
continue;
else
{
SequenceStack->Top++;
break;
}
}
}
//判断匹配后的左右括号数量是否一致
if(SequenceStack->Top == -1)
printf("The string is valid!\n");
else
printf("The string is invalid!\n");
return;
}
代码整体展示:
/*******************************************************************
*
* file name: SequenceStack_demo.c
* author : 790557054@qq.com
* date : 2024/04/25
* function : 该案例是利用顺序栈实现判断一个字符串是否有效,即通过判断
括号数是否能够正确匹配得出结论
* note : None
*
* CopyRight (c) 2023-2024 790557054@qq.com All Right Reseverd
*
* *****************************************************************/
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <string.h>
//指的是顺序栈中的元素的数据类型,用户可以根据需要进行修改
typedef char DataType_t;
//构造记录顺序栈SequenceStack各项参数(栈底地址+栈容量+栈顶元素的下标)的结构体
typedef struct SequenceStack
{
DataType_t * Bottom; //记录栈底地址
unsigned int Size; //记录栈容量
int Top; //记录栈顶元素的下标
}SeqStack_t;
/*********************************************************************
*
* name : SeqStack_Create
* function : 创建一个空的顺序栈,并为记录顺序栈信息的结构体
申请堆内存,并进行初始化即可!
* argument :
* @size :栈的容量大小
*
* retval : 调用成功返回顺序栈的地址
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
//创建顺序表并对顺序栈进行初始化
SeqStack_t * SeqStack_Create(unsigned int size)
{
//1.利用calloc为顺序栈的管理结构体申请一块堆内存
SeqStack_t *Manager = (SeqStack_t *)calloc(1,sizeof(SeqStack_t));
if(NULL == Manager)
{
perror("calloc memory for manager is failed");
exit(-1); //程序异常终止
}
//2.利用calloc为所有元素申请堆内存
Manager->Bottom = (DataType_t *)calloc(size,sizeof(DataType_t));
if (NULL == Manager->Bottom)
{
perror("calloc memory for Stack is failed");
free(Manager);
exit(-1); //程序异常终止
}
//3.对管理顺序栈的结构体进行初始化(元素容量 + 最后元素下标)
Manager->Size = size; //对顺序栈中的容量进行初始化
Manager->Top = -1; //由于顺序栈为空,则栈顶元素的下标初值为-1
return Manager;
}
/*********************************************************************
*
* name : SeqStack_IsFull
* function : 判断顺序栈是否已满
* argument :
* @Manager :顺序栈的地址
*
* retval : 调用成功返回bool型,满了则返回true,没满返回false
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
bool SeqStack_IsFull(SeqStack_t *Manager)
{
return (Manager->Top + 1 == Manager->Size) ? true : false;
}
/*********************************************************************
*
* name : SeqStack_Push
* function : 根据栈的特性,把新元素从栈顶入栈,也就是从数组的尾部进行元素插入
* argument :
* @Manager :顺序栈的地址
@Date :要入栈的数据
*
* retval : 调用成功返回bool型,满了则返回true,没满返回false
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
//入栈
bool SeqStack_Push(SeqStack_t *Manager, DataType_t Data)
{
//1.判断顺序栈是否已满
if ( SeqStack_IsFull(Manager) )
{
printf("SeqStack Full is Full!\n");
return false;
}
//2.如果顺序栈有空闲空间,则把新元素添加到顺序栈的栈顶
Manager->Bottom[++Manager->Top] = Data;
return true;
}
/*********************************************************************
*
* name : SeqStack_IsEmpty
* function : 判断顺序栈是否为空
* argument :
* @Manager :顺序栈的地址
*
* retval : 调用成功返回bool型,空了则返回true,没空返回false
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
bool SeqStack_IsEmpty(SeqStack_t *Manager)
{
return (-1 == Manager->Top) ? true : false;
}
/*********************************************************************
*
* name : SeqStack_Pop
* function : 根据栈的特性,把元素从栈顶出栈,也就是把元素从数组的尾部把元素删除
* argument :
* @Manager :顺序栈的地址
*
* retval : 调用成功返回新的栈地址
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
//出栈
DataType_t SeqStack_Pop(SeqStack_t *Manager)
{
DataType_t temp = 0; //用于存储出栈元素的值
//1.判断顺序栈是否为空
if ( SeqStack_IsEmpty(Manager) )
{
// printf("SeqStack is Empty!\n");
return -1;
}
//2.由于删除了一个元素,则需要让顺序栈的栈顶元素下标-1
temp = Manager->Bottom[Manager->Top--];
return temp;
}
/*********************************************************************
*
* name : SeqStack_JudgString
* function : 根据用户输入的字符串中的括号个数与匹配度进行判断字符串的
正确性
* argument :
* @Manager :顺序栈的地址
*
* retval : 调用成功返回新的栈地址
* author : 790557054@qq.com
* date : 2024/04/25
* note : none
*
* *****************************************************************/
void SeqStack_JudgString( DataType_t *str)
{
//创建顺序栈
SeqStack_t *SequenceStack = SeqStack_Create(sizeof(str));
//计算得到的字符串长度
int n = strlen(str);
//遍历得到的字符串,将字符串中各中类型的左括号按先后顺序放入顺序栈中
for (int i = 0; i < n;i++)
{
if(str[i] == '(')
SeqStack_Push(SequenceStack, str[i]);
else if(str[i] == '[')
SeqStack_Push(SequenceStack, str[i]);
else if(str[i] == '{')
SeqStack_Push(SequenceStack, str[i]);
}
//再次对字符串遍历,找到对应的右括号,并且判断类型是否相符合
for (int i = 0; i < n; i++)
{
if(str[i] == ')')
{
DataType_t temp = SeqStack_Pop(SequenceStack);
if('('== temp) //弹栈出的元素是相同类型的左括号时,继续遍历
continue;
else
{
SequenceStack->Top++;
break;
}
}
else if(str[i] == ']')
{
DataType_t temp1 = SeqStack_Pop(SequenceStack);
if('[' == temp1)
continue;
else
{
SequenceStack->Top++;
break;
}
}
else if(str[i] == '}')
{
DataType_t temp2 = SeqStack_Pop(SequenceStack);
if('{'== temp2)
continue;
else
{
SequenceStack->Top++;
break;
}
}
}
//判断匹配后的左右括号数量是否一致
if(SequenceStack->Top == -1)
printf("The string is valid!\n");
else
printf("The string is invalid!\n");
return;
}
int main(int argc, char const *argv[])
{
while(1)
{
//定义一个字符串指针变量 用于存储用户输入的字符串
DataType_t str[200];
printf("Please input a string containing parentheses :\n ");
scanf("%s", str);
SeqStack_JudgString( str);
}
return 0;
}
结果验证:

待优化问题:
- 如果右括号在最前面时,应该判断是无效,但是目前算法无法判断,例如:)(1+2 该算法会判断有效 是错误判断
优化思路:
将判断’(‘和 ’)‘的判断放进一个循环里面判断,这样比两次遍历的时间复杂度更低,需要吸取教训,优化自身解题思路,思考更多样的情况。
图示:文章来源:https://www.toymoban.com/news/detail-858648.html
 文章来源地址https://www.toymoban.com/news/detail-858648.html
文章来源地址https://www.toymoban.com/news/detail-858648.html
到了这里,关于练习题----顺序栈算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!