3d世界坐标转换到某个二维平面。-Toy模板网

这篇具有很好参考价值的文章主要介绍了3d世界坐标转换到某个二维平面。。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

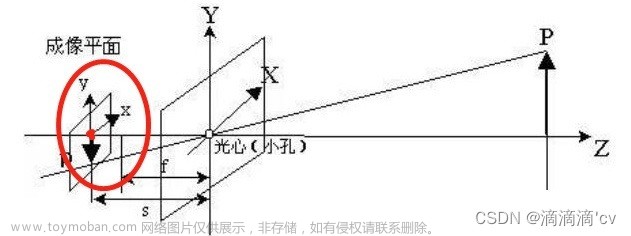
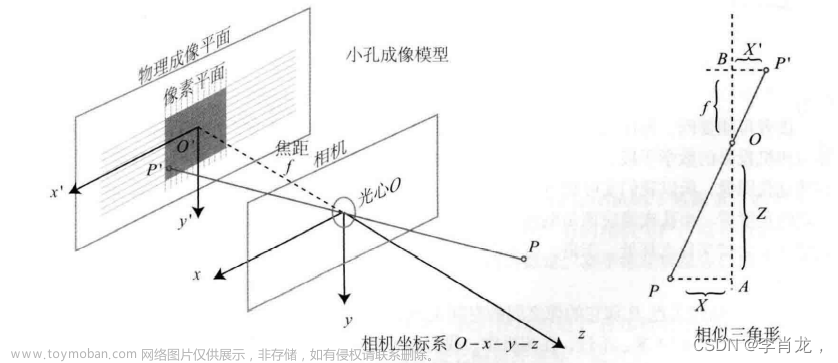
有个功能需要截取某个平面的点云数据，然后计算宽高。需要将3d点投影到二维平面上。文章来源地址https://www.toymoban.com/news/detail-858749.html

        //将3d坐标点转换为2d
        /**
         * 法向量(A, B, C)
         * 常量D
         * 原点x0,y0,z0
         * 方向向量(vx, vy, vz)
         * 投影点(x,y,z)
         * 
public static double[] Convert3DPointTo2D(
            double A, double B, double C, double D,
            double x0, double y0, double z0,
            double vx, double vy, double vz,
            double x, double y, double z)
        {
            // 首先，找到平面P上的两个正交向量
            // 我们可以使用平面的法向量(A, B, C)和L1的方向向量(vx, vy, vz)的叉积来找到平面上的一个向量
            double ux = B * vz - C * vy;
            double uy = C * vx - A * vz;
            double uz = A * vy - B * vx;

            // 规范化这个向量得到U（我们2D坐标系统中的x轴）
            double lengthU = Math.Sqrt(ux * ux + uy * uy + uz * uz);
            ux /= lengthU;
            uy /= lengthU;
            uz /= lengthU;

            // 要找到第二个向量，我们可以取U和平面的法向量的叉积
            double vx2 = uy * C - uz * B;
            double vy2 = uz * A - ux * C;
            double vz2 = ux * B - uy * A;

            // 规范化这个向量得到V（我们2D坐标系统中的y轴）
            double lengthV = Math.Sqrt(vx2 * vx2 + vy2 * vy2 + vz2 * vz2);
            vx2 /= lengthV;
            vy2 /= lengthV;
            vz2 /= lengthV;




            // 现在，我们可以将点(x, y, z)投影到平面上，并计算其在2D系统中的坐标
            // 计算点到平面的投影
            double t = -(A * x + B * y + C * z + D) / (A * A + B * B + C * C);
            double xp = x + A * t;
            double yp = y + B * t;
            double zp = z + C * t;

            // 计算投影点在平面坐标系统中的2D坐标(u, v)
            double u = (xp - x0) * ux + (yp - y0) * uy + (zp - z0) * uz;
            double v = (xp - x0) * vx2 + (yp - y0) * vy2 + (zp - z0) * vz2;
            return new double[] { u, v };
        }

到了这里，关于3d世界坐标转换到某个二维平面。的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！