最大子矩阵（openjudge noi-2.6基本算法之动态规划-1768）-Toy模板网

这篇具有很好参考价值的文章主要介绍了最大子矩阵（openjudge noi-2.6基本算法之动态规划-1768）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

（1）题目

来源

OpenJudge - 1768:最大子矩阵

题目描述

已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，你的任务是找到最大的非空(大小至少是1 * 1)子矩阵。

比如，如下4 * 4的矩阵

0        -2        -7        0
9       2        -6        2
-4         1        -4        1
-1       8        0       -2

它的最大子矩阵是

9         2
-4         1
-1         8

这个子矩阵的大小是15。

输入格式

输入是一个N * N的矩阵。输入的第一行给出N (0 < N <= 100)。再后面的若干行中，依次（首先从左到右给出第一行的N个整数，再从左到右给出第二行的N个整数……）给出矩阵中的N²个整数，整数之间由空白字符分隔（空格或者空行）。已知矩阵中整数的范围都在[-127, 127]。

输出格式

输出最大子矩阵的大小。

输入样例

4

0        -2        -7        0
9       2        -6        2
-4         1        -4        1
-1       8        0       -2

输出样例

15

（2）思路

1. 分析问题：分析已知和未知

这道题和最大子段和有所相同，但变成二维的了，推荐看这道题题解的小伙伴们先去看一下我的另一篇题解——最大子段和

最大子段和（洛谷--P1115）-CSDN博客

我们将进行以下几步：a. 枚举；b. 前缀和。

最大子矩阵（openjudge noi-2.6基本算法之动态规划-1768）,算法,动态规划进入分析环节

a. 枚举

你以为我们会枚举四个顶点或一个顶点和矩阵长宽或左上顶点和右下顶点吗？

错！！！你想想那要写多少层循环！！！

如果真那么写，会是这样(从举的例子中可见，枚举左上顶点和右下顶点的时间复杂度应该少一点，那就枚举左上顶点和右下顶点得到所有子矩阵，求和再比较)

#include<iostream>
using namespace std;
int main()
{
	int n,a[105][105],maxi=-130;//矩阵中整数的范围都在[-127, 127],maxi=-130
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++) cin>>a[i][j]; //熟人 
	} 
	for(int x1=1;x1<=n;x1++)
	{
		for(int y1=1;y1<=n;y1++)//枚举左上顶点 
		{
			for(int x2=x1;x2<=n;x2++)
			{
				for(int y2=y1;y2<=n;y2++)//枚举右下顶点 
				{
					int sum=0;
					for(int i=x1;i<=x2;i++)
					{
						for(int j=y1;j<=y2;j++) sum+=a[i][j];//求和 
					}
					maxi=max(sum,maxi);//比较，求最大值 
				}
			}
		}
	}
	cout<<maxi; 
	return 0;
}

你说这超不超时。

看来，只枚举是不行了

b. 前缀和

根据最大子段和的思路，我们可以先求出第一行第一列到剩下每个位置的子矩阵的和，再通过拼图的思路求和

for(int i=1;i<=n;i++)

{

for(int j=1;j<=n;j++)//枚举各个位置

{

for(int m=1;m<=i;m++)//枚举第一行第一列到此位置的子矩阵

{

for(int n=1;n<=j;n++) f[i][j]+=a[x][y];//求前缀和

}
}
}//求前缀和

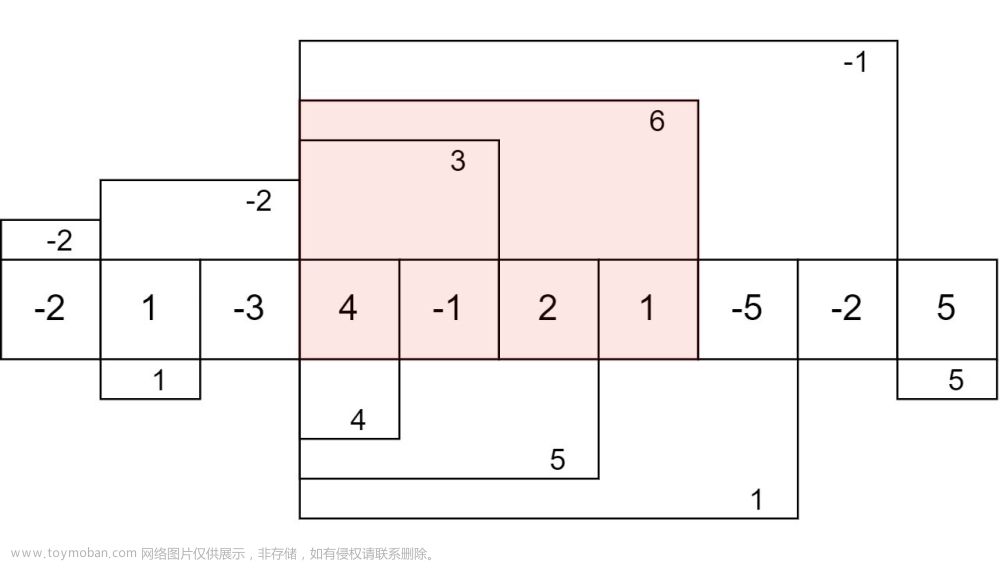
拼图的思路作图如下

最大子矩阵（openjudge noi-2.6基本算法之动态规划-1768）,算法,动态规划

假如，若要求红框内矩阵的和，要用(1，1)到红框内矩阵的右下角的矩阵的和(蓝框)，减去剩下的部分，可以先减去橙框和绿框，再把橙框和绿框重叠的部分加回来(因为它被减了2次)，就可以得到红框内矩阵的和了

修改内容：

有没有觉得4重循环还是多了？

前缀和的内容还可以简化哦！

但简化后的内容也要运用拼图思路

如图所示

最大子矩阵（openjudge noi-2.6基本算法之动态规划-1768）,算法,动态规划

如果要求红框矩阵内的和，可以用（黄框+绿框-重叠部分+蓝圈=红框）的公式求和。

可以这样做的原因是，黄框和绿框以及重叠部分已经求过了！！！再加上蓝圈(a[i])就可以了。

具体代码如下

for(int i=1;i<=n;i++)

{

        for(int j=1;j<=n;j++)

        {

                f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j];//拼图思路
        }
}

2. 数据定义：已知和未知的取名和类型

n：输入是一个N * N的矩阵

a[105][105]：输入的矩阵，0 < n <= 100

f[105][105]：第一行第一列到剩下每个位置的子矩阵的和，0 < n <= 100

sum：所有子矩阵的和

maxi：所有子矩阵中最大和，矩阵中整数的范围都在[-127, 127]

3. 数据输入：输入已知

cin>>n;

for(int i=1;i<=n;i++)

{

for(int j=1;j<=n;j++) cin>>a[i][j];

}

4. 数据计算：数字建模+设计算法

找前缀和的代码在前面已经给大家讲过了，下面是拼图的思路

for(int r1=1;r1<=n;r1++)

{

        for(int c1=1;c1<=n;c1++)//枚举左上顶点

{

                for(int r2=r1;r2<=n;r2++)

{

                        for(int c2=c1;c2<=n;c2++)枚举右下顶点

{

                                sum=f[r2][c2]+f[r1-1][c1-1]-f[r1-1][c2]-f[r2][c1-1];//拼图求和

                                maxi=max(maxi,sum);//比较

sum=0;//清零

}

}
}
}文章来源地址https://www.toymoban.com/news/detail-858894.html

（3）完整AC代码

#include<iostream>
using namespace std;
int main()
{
	int f1[105][105]={0};
	int n,a[105][105],f[105][105]={0},sum=0,maxi=-0x3f3f3f3f;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++) cin>>a[i][j];
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j];
		}
	}
	for(int r1=1;r1<=n;r1++)
	{
		for(int c1=1;c1<=n;c1++)
		{
			for(int r2=r1;r2<=n;r2++)
			{
				for(int c2=c1;c2<=n;c2++)
				{
					sum=f[r2][c2]+f[r1-1][c1-1]-f[r1-1][c2]-f[r2][c1-1];
					maxi=max(maxi,sum);
					sum=0;
				}
			}
		}
	}
	cout<<maxi;
	return 0;
}

到了这里，关于最大子矩阵（openjudge noi-2.6基本算法之动态规划-1768）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！