动态规划完全背包问题-java-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划完全背包问题-java。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

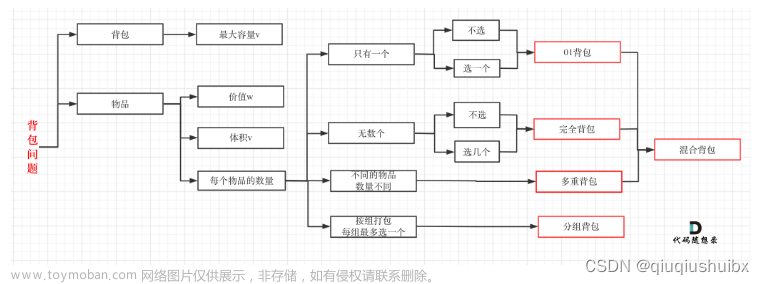
完全背包问题跟01背包问题思路大致一样，只不过对于物品的拿取次数不在限制，我们只需要考虑这点即可。

文章目录

前言

一、什么是完全背包问题？

二、问题模拟

1.样例数据

2.算法思路

三、代码如下

1.代码如下（示例）：

2.读入数

3.代码运行结果

总结

前言

完全背包问题跟01背包问题思路大致一样，只不过对于物品的拿取次数不在限制，我们只需要考虑这点即可。

提示：以下是本篇文章正文内容，下面案例可供参考

一、什么是完全背包问题？

有n种物品和一个bag大小的背包容量，每种物品都有无限件可以使用，每个物品都有体积v和价值w，求解背包所能容纳的最大价值是多少？

二、问题模拟

1.样例数据

假设我们还有有4种物品和一个容量为5的背包，这四种物品对应的体积和价值分别为：

物品一：体积是1，价值是2
物品二：体积是2，价值是4
物品三：体积是3，价值是4
物品三：体积是4，价值是5

2.算法思路

数组v[i]表示第i种物品的体积，w[i]表示第i种物品的价值。

我们引入dp状态数组，行数i表示第几种物品，列数j表示背包的容量j，dp[i][j] 表示在当前背包容量j下选取第i种物品后所能容纳的最大价值。

dp[i][j]的计算可以通过以下的推算进行：

选取0个第i种物品即不选取新物品，即对应
选取1个第i种物品， $完全背包问题java代码,动态规划,算法,java$
选取2个第i种物品， $完全背包问题java代码,动态规划,算法,java$

上述过程不会无限增加，因为我们有背包容量j，那么我们就可以得到一个极限条件，假设当前背包容量j下最多可得到t个物品，

那么完全背包的状态就是我们在不拿新物品、拿1件新物品、拿2件新物品等等直到最多拿k件新物品中比较得到的最大值即为dp[i][j]的值

$完全背包问题java代码,动态规划,算法,java$

那么我们就可以得到dp数组的递推代码：

        //第几种物品
        for(int i = 1;i <= n;i++){
            //背包容量
            for(int j = 1;j <= bag;j++){
                //表示在当前背包容量j下最多再放t个第i种物品
                int t = j / v[i];
                for(int k = 0;k <= t;k++){
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-k*v[i]] + w[i] * k);
                }
            }
        }

3.代码优化

我们通过观察可以发现，其实k循环可以舍弃掉，完全背包问题dp[i][j]我们可以通过每次累加v[i]，当j < v[i],我们相当于没加取上一个物品的最佳状态，dp[i][j] = dp[i-1][j]。当j >= v[i]，那我们就取当前第i个物品然后背包容量j-v[j]时的最大价值+w[i]，dp = max{dp[i-1][j],dp[i][j-v[i]]+w[i]}

        //第几种物品
        for(int i = 1;i <= n;i++){
            //背包容量
            for(int j = 1;j <= bag;j++){
                dp[i][j] = dp[i-1][j];
                if(j - v[i] >= 0){
                    dp[i][j] = Math.max(dp[i][j],dp[i][j-v[i]]+w[i]);
                }
            }
        }

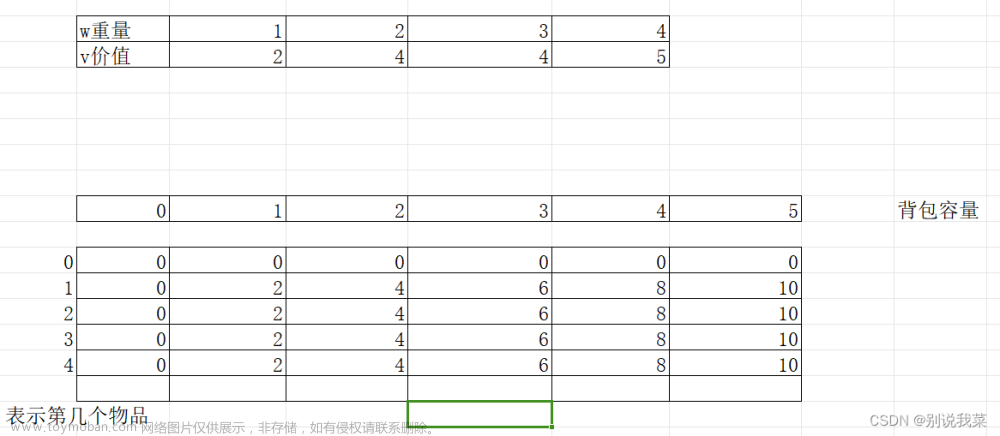
完全背包问题java代码,动态规划,算法,java

图2.1dp数组值

三、代码如下

1.代码如下（示例）：

package AcWing;

import java.io.*;

public class 完全背包问题 {
    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static void main(String[] args) throws Exception{
        int n = nextInt(),bag = nextInt();
        int[][] dp = new int[n+1][bag+1];
        //体积
        int[] v = new int[n+1];
        //价值
        int[] w = new int[n+1];
        for(int i = 1;i <= n;i++){
            v[i] = nextInt();
            w[i] = nextInt();
        }
        //第几种物品
        for(int i = 1;i <= n;i++){
            //背包容量
            for(int j = 1;j <= bag;j++){
                //表示在当前背包容量j下最多再放t个第i种物品
                int t = j / v[i];
                for(int k = 0;k <= t;k++){
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-k*v[i]] + w[i] * k);
                }
            }
        }
        pw.println(dp[n][bag]);
        pw.flush();
    }
    public static int nextInt()throws Exception{
        st.nextToken();
        return (int)st.nval;
    }
}