矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵-Toy模板网

这篇具有很好参考价值的文章主要介绍了矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

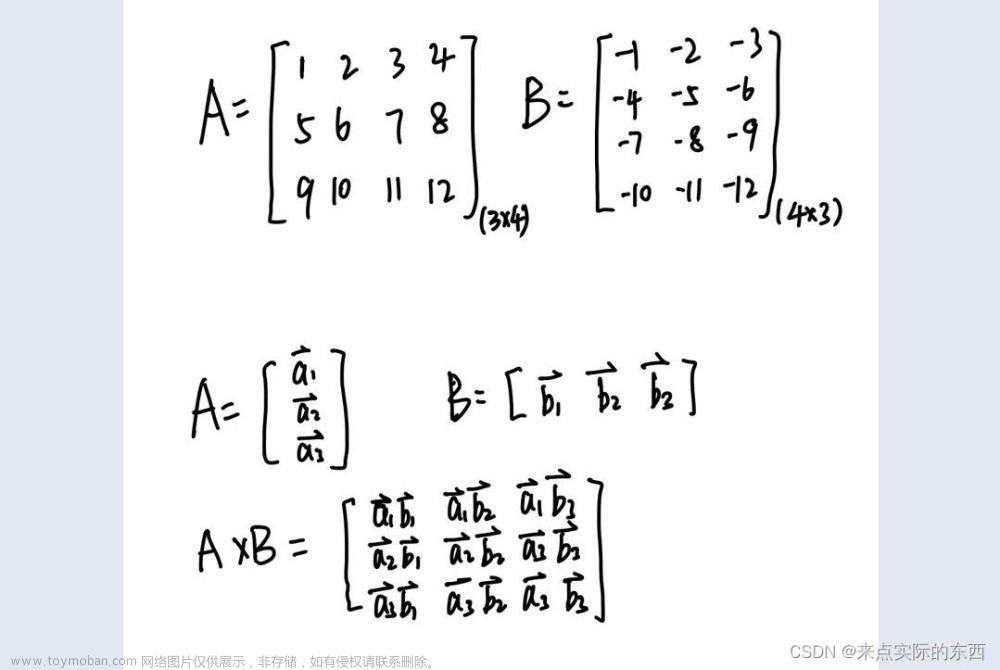
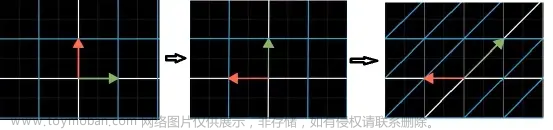
论文自然还是 Anatomy of High-Performance Matrix Multiplication。

如何拆分

一个矩阵乘法有 6 种拆分方式，其中对 row-major 效率最高的是：

矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵,矩阵,线性代数,c++

第一次拆分

先做第一次拆分，取 A 的 kc 列（PanelA）和 B 的 kc 行（PanelB），得到待累加的一部分结果；

矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵,矩阵,线性代数,c++

第二次拆分

第二次拆分，把 PanelB 按 nc 大小切分成多个 BlockB，分别与 PanelA 相乘；

矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵,矩阵,线性代数,c++

第三次拆分

最后一次切分，把 PanelA 按 mr 大小切分，与 BlockB 乘（注意具体代码里的kernel4x4或者kernel8x8是指 mr 的大小）。

GEPB 约束条件

我们考察最后一次 GEPB 的切分过程，如何使其性能最高？

矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵,矩阵,线性代数,c++

GEPB参数

以上是 GEPB 的参数，如果这个运算所需数据都加载到 L1 cache 里，那计算效率自然是最高的。此时运算 ops 为 2∗m∗kc∗nc ，同时做的数据搬运量为 kc∗nc+m(kc+2nc) ，我们期望做最小的 io 产生最大的计算，即

max(2∗m∗kc∗nc/(kc∗nc+m(kc+2nc)))

由于 nc 远小于 m，上式约等于

maximize(2∗kc∗nc/(kc+2∗nc))

可以得到以下约束/倾向：

约束1: maximize(2∗kc∗nc/(kc+2∗nc))

约束2：kc*nc 越大效果越好

Cache 层级分配

由于 L1Cache 通常比较小，不太可能得到比较大的 kc∗nc kc∗nc 值，是否可能把 BlockB 放到 L2Cache 里，尽量让 kc∗nc 最大？已知 GEPB 计算的伪代码为

Load PanelB into cache
for j = 0...M-1
  Load Aj into cache
  Load Cj into cache
  subkernel_calculation
  Store Cj
endfor

循环里每次取 PanelA 的 mr 行做计算，每次计算的时间开销为

2∗mr∗kc∗nc/cpu_frequency

假设 PanelB 放入了 L2Cache，每次加载需要的时间为
kc∗nc/l2cache_speed

计算时间要大于加载时间，才能防止 CPU 等待 IO 从而让 CPU ALU 跑满，代入上式可得到约束条件

约束3：mr≥cpu_frequency/(l2cache_speed∗2)

因为计算用的数据都在 L1Cache，所以每次从 PanelA 加载的 nr 行不宜超过 L1Cache大小。同时计算结果 C 也需要空间，可以得到

约束4： mr∗kc≤l1_cachesize/2

当数据全放到了 L1Cache 里计算时，每次是用 kernel4x4 还是 kernel8x8，取决于 CPU 有多少寄存器。一般是尽可能利用所有 reg。可以得到

约束5：nr kr 的选择完全看寄存器情况

需要一半的寄存器存结果
nr 和 kr 接近，效果最佳
armv8 浮点一般是、8x8

来自 TLB 的约束

我们知道计算机存储结构长这个样子

矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵,矩阵,线性代数,c++

计算机存储结构

上文说到要把 BlockB 放到 L2Cache，随着 ALU 的计算不断加载到 L1Cache。实际上两个 Cache 中间还隔着个 TLB，因此要考虑 TLB 寻址空间的限制。L1Cache miss 可以用 prefetch 指令处理掉，TLB miss 会真的 stall CPU，影响 ALU 利用率。

Cache 寻址空间（256K）一般小于 L2Cache 大小（2M），因此有

约束6： GEPB内循环一次计算所需数据总大小（的行的行BlockB+A的mr行+C的mr行）不能超过 TLB 寻址空间

约束7：计算数据要 Packing，防止 TLB miss

总结一下行主序 GEMM 分块的参数选择

mr、nr 和 kr 如何取值

尽可能是个正方形，尽量用满寄存器
约束3 限制了 mr 的最小值

kc 的取值

nc*kc 尽可能大，但不能大过 TLB 寻址空间的一半
kc 不超过 l1_cachesize/2/mr ，其中 mr 已在上文选取
按经验是页表大小的一半，即 pagesize/2

nc 的取值

nc=kc ，参见约束1

mc 的取值

mc∗k<l2_cachesize 我们期望 A 尽可能放到 L2Cache 里面

就已知的情况来看，fp32 GEMM 极限可达到 10-11 gflops 左右（即 CPU 峰值的 80+%，packA 和 packB 开销跟着矩阵形状走大约是20%），结合具体的任务，例如 2D 卷积、全连接，可以做到 90% 左右。文章来源地址https://www.toymoban.com/news/detail-859509.html

到了这里，关于矩阵乘法优化：GEMM中如何将大矩阵切割成小矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！