动态规划可以理解为递归,只不过递归是通过函数实现,动态规划通过循环实现!
一、前言
动态规划有多好用我就不过多介绍,写这篇文章的时候我也不是熟练掌握,只是单纯记录一下我的学习经历并分享一些我的心得体会,仅此而已。
推荐看一下这个视频,对你的理解应该会有所帮助。
二、基本思想
动态规划最核心的思想,就在于拆分子问题,记住过往,减少重复计算。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案(所谓的DP数组)。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
三、解题步骤
这或许会包含各种各样的例题,我想从中进行对比以达成熟练掌握的目的,持续更新。。。
大致步骤如下:
- 穷举分析
- 确定边界
- 找规律,确定最优子结构
- 状态转移方程
例题一(最长递增子序列)

1、穷举分析
自顶向上的穷举
这里观察规律,显然是有关系的,我们还是遵循动态规划自底向上的原则,基于示例1的数据,从数组只有一个元素开始分析。
- 当nums只有一个元素10时,最长递增子序列是[10],长度是1.
- 当nums需要加入一个元素9时,最长递增子序列是[10]或者[9],长度是1。
- 当nums再加入一个元素2时,最长递增子序列是[10]或者[9]或者[2],长度是1。
- 当nums再加入一个元素5时,最长递增子序列是[2,5],长度是2。
- 当nums再加入一个元素3时,最长递增子序列是[2,5]或者[2,3],长度是2。
- 当nums再加入一个元素7时,,最长递增子序列是[2,5,7]或者[2,3,7],长度是3。
- 当nums再加入一个元素101时,最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是4。
- 当nums再加入一个元素18时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。
- 当nums再加入一个元素7时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。
通过上面分析,我们可以发现一个规律:
如果新加入一个元素nums[i], 最长递增子序列要么是以nums[i]结尾的递增子序列,要么就是nums[i-1]的最长递增子序列。
原问题数组nums[i]的最长递增子序列 = 子问题数组nums[i-1]的最长递增子序列/nums[i]结尾的最长递增子序列
所以原问题,我们转化成求出以数组nums每个元素结尾的最长子序列集合,再取最大值。

2、确定边界
当nums数组只有一个元素时,最长递增子序列的长度dp(1)=1,当nums数组有两个元素时,dp[2] =2或者1, 因此边界就是dp[1]=1。
3、最优子结构
从穷举分析,我们可以得出,以下的最优结构:
dp[i] = max(dp[j]) + 1,存在j属于区间[0,i-1],并且num[i] > num[j]。
max(dp[j]) 就是最优子结构。
4、状态转移方程
dp[i] = Math.max(dp[i], dp[j] + 1);5、代码实现
class Solution {
public int lengthOfLIS(int[] nums) {
int n=nums.length;
if(n==1) return 1;
if(n==0) return 0;
int[] dp=new int[n];
int res=0;
Arrays.fill(dp,1);
for(int i=1;i<n;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j])
{
dp[i]=Math.max(dp[i],dp[j]+1);
}
res=Math.max(res,dp[i]);
}
}
return res;
}
}
6、复杂度
时间复杂度O(n^2),空间复杂度O(n)
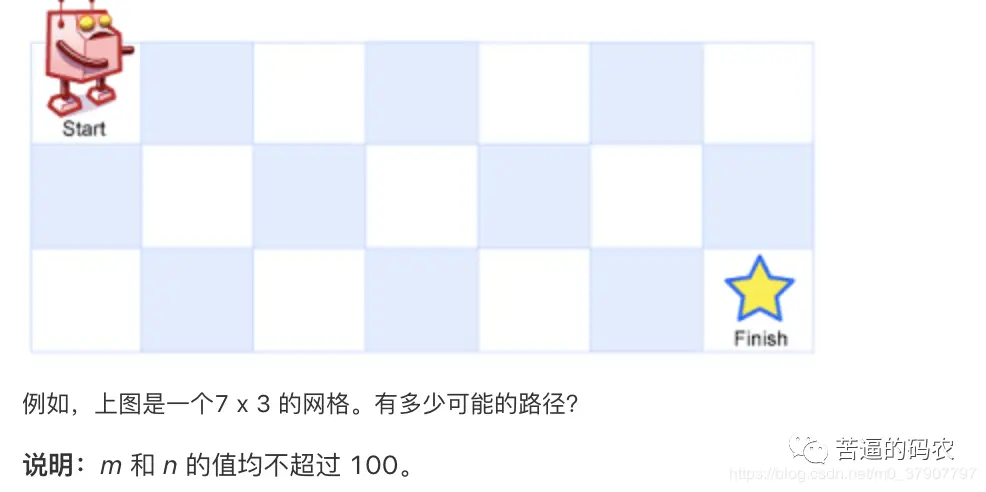
例题二(过河卒)

1、分析
卒只能向下和向右走,所以当前点等于上面的点加左边的点的可能数
2、确定边界
显然,dp[0][0] = 1
3、状态转移方程
if (d[i][j] != -1) {
if (i) dp[i][j] += dp[i - 1][j];
if (j) dp[i][j] += dp[i][j - 1];
}4、AC代码
#include<bits/stdc++.h>
#define MAX 30
using namespace std;
int d[MAX][MAX] = { 0 };
long long dp[MAX][MAX] = { 0 };//开long long防止数值过大
//用于马的控制点赋值
const int dx[] = { 2,1,-1,-2,-2,-1,1,2 };
const int dy[] = { 1,2,2,1,-1,-2,-2,-1 };
int main() {
int bx, by, mx, my;
cin >> bx >> by >> mx >> my;
/*for (int i = 1; i < bx; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < by; i++) {
dp[0][i] = 1;
}*/
d[mx][my] = -1;
for (int i = 0; i < 8; i++) {//马控制点赋值
if (mx + dx[i] >= 0 && mx + dx[i] <= bx && my + dy[i] >= 0 && my + dy[i] <= by) {
d[mx + dx[i]][my + dy[i]] = -1;
}
}
dp[0][0] = 1;
for (int i = 0; i <= bx; i++) {//卒只能向下和向右走,所以当前点等于上面的点加左边的点的可能数
for (int j = 0; j <= by; j++) {
if (d[i][j] != -1) {
if (i) dp[i][j] += dp[i - 1][j];
if (j) dp[i][j] += dp[i][j - 1];
}
}
}
//打印地图和dp
/*for (int i = 0; i <= by; i++) {
for (int j = 0; j <= bx; j++) {
cout << d[i][j]<< " ";
if (j == bx) {
cout << endl;
}
}
}
cout << endl;
for (int i = 0; i <= by; i++) {
for (int j = 0; j <= bx; j++) {
cout << dp[i][j] << " ";
if (j == bx) {
cout << endl;
}
}
}*/
cout << dp[bx][by] << endl;
return 0;
}例题三(摆花)

1、分析
定义状态:f(i,j) 表示前 i 个数总和为 j 的方案数。
2、状态转移方程
f(i,j)=f(i−1,j−k) (k从0到a[i])
其中, k是枚举当前第 i 个数的取值。
3、复杂度
时间复杂度:O(nmai),稳得一批。
空间复杂度:O(nm)
4、代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105, mod = 1000007;
int n, m, a[maxn], f[maxn][maxn];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
f[0][0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= min(j, a[i]); k++)
f[i][j] = (f[i][j] + f[i - 1][j - k]) % mod;
cout << f[n][m] << endl;
return 0;
}例题四(李白打酒加强版)


1、分析
设 f[i][j][k] 为当前走到第 i 个位置,看了 j 次花,有 k 斗酒的方案数。
题目中说了初始两斗酒,那么 f[0][0][2]=1。
重点是怎么前推后,依次循环 i,j,k,
如果 f[i][j][k] 不是 0,那么我们在第 i+1 个位置看花或者经过酒店。
看花:走到第 i+1 个位置,看了 j+1 次花,酒的数量变为 k−1。
酒馆:走到第 i+1 个位置,看了 j 次花,酒的数量变为 k×2。
2、状态转移方程
if (f[i][j][k] != 0)//这里也可以简写成 if(f[i][j][k])
{
f[i + 1][j + 1][k - 1] += f[i][j][k];
f[i + 1][j][k * 2] += f[i][j][k];
}j 只需要循环到 m−1,不需要循环到 m,如果循环到了 m:
首先,再看花变成 m+1 已经对答案没有任何的贡献了。
其次,这样还会多算。如果不看花只能是没有酒,一直经过酒店,
但是题目要求最后一次只能经过花,所以不行。
还有一个问题:酒的斗数上限是什么?文章来源:https://www.toymoban.com/news/detail-859591.html
显然不会超过 m,不然最后的酒就喝不完了,所以也循环到 m。文章来源地址https://www.toymoban.com/news/detail-859591.html
3、代码
#include <iostream>
using namespace std;
int n, m;
int f[205][105][105];
int main() {
cin >> n >> m;
f[0][0][2] = 1;
for (int i = 0; i < n + m; i ++)
for (int j = 0; j < m; j ++)
for (int k = 0; k <= m; k ++)
if (f[i][j][k]) {
if (k > 0)
f[i + 1][j + 1][k - 1]
= (f[i + 1][j + 1][k - 1] + f[i][j][k]) % 1000000007;
if (k <= 50)
f[i + 1][j][k * 2]
= (f[i + 1][j][k * 2] + f[i][j][k]) % 1000000007;
}
cout << f[n + m][m][0];
return 0;
}到了这里,关于浅析动态规划(Dynamic Programming,DP)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!