探索树与二叉树：从基础到应用的完整指南

目录

一.树的基本概念

 二.二叉树的概念

三.二叉树的遍历和线索二叉树

 四.树和森林

五.树与二叉树的应用

六.实际案例

七.总结

一.树的基本概念

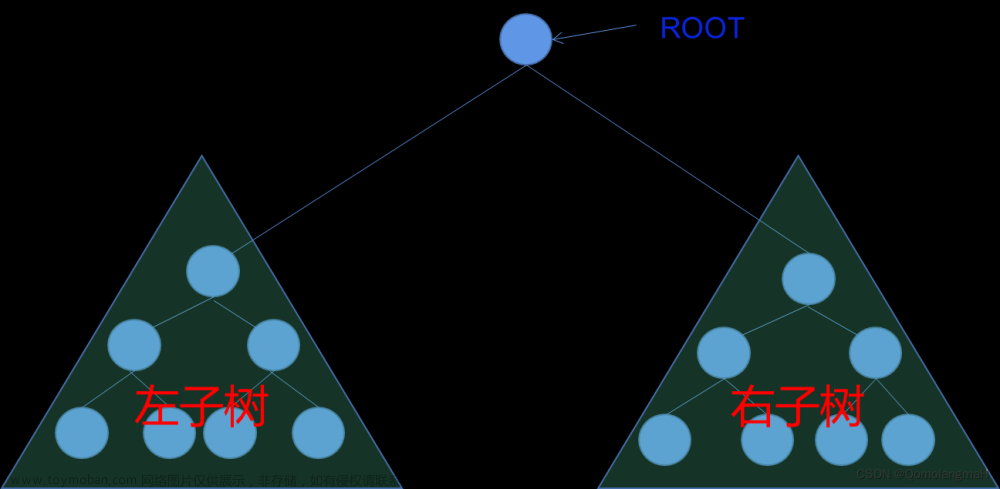
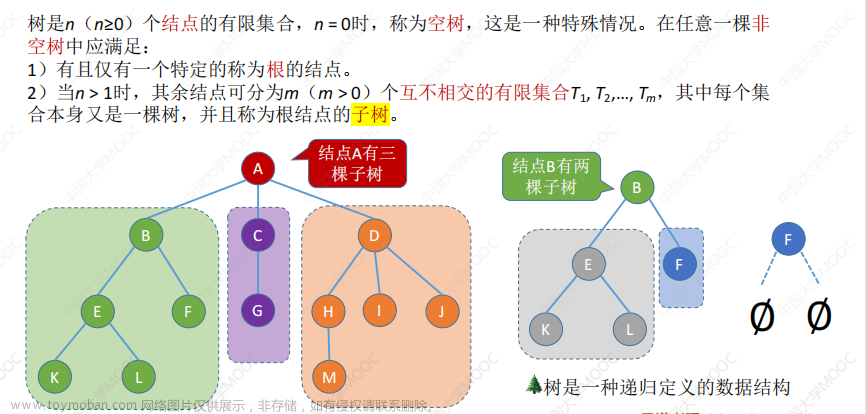
        树是一种非线性的数据结构，由节点和边组成的有限集合。树的结构类似于自然界中的树，从根部开始，向上延伸出许多分支，每个节点可以有零个或多个子节点，但每个节点只有一个父节点（除了根节点）。根节点是树中的顶部节点，没有父节点。

树的特点包括：

• 每个节点可以有零个或多个子节点。
• 每个节点只有一个父节点（除了根节点）。
• 树中没有环路，即不能存在从一个节点出发经过若干条边回到原始节点的路径。

以下是实现树的c++代码

#include <iostream>
#include <vector>
#include <string>
using namespace std;
// 树节点类
class TreeNode {
public:
    string value;
    vector<TreeNode*> children;
    // 构造函数
    TreeNode(string val) : value(val) {}
    // 添加子节点
    void add_child(TreeNode* child) {
        children.push_back(child);
    }
};
// 打印树的结构
void print_tree(TreeNode* node, int level = 0) {
    cout << string(level * 2, ' ') << node->value << endl;
    for (TreeNode* child : node->children) {
        print_tree(child, level + 1);
    }
}
int main() {
    // 创建树的示例
    TreeNode* root = new TreeNode("A");
    // 添加子节点
    root->add_child(new TreeNode("B"));
    root->add_child(new TreeNode("C"));
    root->add_child(new TreeNode("D"));

    // 添加子节点的子节点
    root->children[0]->add_child(new TreeNode("E"));
    root->children[0]->add_child(new TreeNode("F"));
    root->children[2]->add_child(new TreeNode("G"));

    // 打印树的结构
    cout << "树的结构：" << endl;
    print_tree(root);

    // 释放内存
    delete root;

    return 0;
}

        树的基本概念简单而清晰，它提供了一种有序的数据组织方式，适用于许多领域的问题建模和解决。在计算机科学中，树的应用非常广泛，例如在文件系统中表示文件的层次结构、在数据库中构建索引、在图形界面中构建UI布局等。

 二.二叉树的概念

        二叉树是一种特殊的树，它的每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树的结构更加规则，因此在计算机科学中广泛应用于各种算法和数据结构。

二叉树的特点包括：

• 每个节点最多有两个子节点。
• 左子节点和右子节点的顺序是固定的，即左子节点始终位于右子节点之前。
• 二叉树可以是空的，即不包含任何节点的情况。

以下是演示二叉树的基本结构的代码

#include <iostream>

using namespace std;

// 二叉树节点类
class BinaryTreeNode {
public:
    int value;
    BinaryTreeNode* left;
    BinaryTreeNode* right;

    // 构造函数
    BinaryTreeNode(int val) : value(val), left(nullptr), right(nullptr) {}
};

// 二叉树类
class BinaryTree {
public:
    BinaryTreeNode* root;

    // 构造函数
    BinaryTree() : root(nullptr) {}

    // 插入节点
    void insert(int val) {
        root = insertNode(root, val);
    }

    // 插入节点的辅助函数
    BinaryTreeNode* insertNode(BinaryTreeNode* node, int val) {
        if (node == nullptr) {
            return new BinaryTreeNode(val);
        }
        if (val < node->value) {
            node->left = insertNode(node->left, val);
        } else {
            node->right = insertNode(node->right, val);
        }
        return node;
    }

    // 中序遍历
    void inorderTraversal(BinaryTreeNode* node) {
        if (node == nullptr) return;
        inorderTraversal(node->left);
        cout << node->value << " ";
        inorderTraversal(node->right);
    }
};

int main() {
    // 创建二叉树示例
    BinaryTree tree;

    // 插入节点
    tree.insert(5);
    tree.insert(3);
    tree.insert(8);
    tree.insert(2);
    tree.insert(4);
    tree.insert(7);
    tree.insert(9);

    // 中序遍历二叉树
    cout << "中序遍历结果：" << endl;
    tree.inorderTraversal(tree.root);
    cout << endl;

    return 0;
}

        二叉树的结构简单清晰，具有良好的可预测性和易于操作性，因此在实际应用中得到广泛的应用。例如，二叉搜索树（Binary Search Tree，BST）是一种常见的数据结构，它利用了二叉树的有序性质，在插入、查找和删除等操作上具有较高的效率。 

三.二叉树的遍历和线索二叉树

遍历是指按照某种顺序访问二叉树中的所有节点。常见的遍历方式有前序遍历、中序遍历和后序遍历。

• 前序遍历：先访问根节点，然后遍历左子树，最后遍历右子树。
• 中序遍历：先遍历左子树，然后访问根节点，最后遍历右子树。
• 后序遍历：先遍历左子树，然后遍历右子树，最后访问根节点。

以下是实现二叉树三种遍历方法的c++代码

#include <iostream>

using namespace std;

// 二叉树节点类
class BinaryTreeNode {
public:
    int value;
    BinaryTreeNode* left;
    BinaryTreeNode* right;

    // 构造函数
    BinaryTreeNode(int val) : value(val), left(nullptr), right(nullptr) {}
};

// 前序遍历二叉树
void preorderTraversal(BinaryTreeNode* node) {
    if (node == nullptr) return;
    cout << node->value << " "; // 先访问根节点
    preorderTraversal(node->left); // 再遍历左子树
    preorderTraversal(node->right); // 最后遍历右子树
}

// 中序遍历二叉树
void inorderTraversal(BinaryTreeNode* node) {
    if (node == nullptr) return;
    inorderTraversal(node->left); // 先遍历左子树
    cout << node->value << " "; // 再访问根节点
    inorderTraversal(node->right); // 最后遍历右子树
}

// 后序遍历二叉树
void postorderTraversal(BinaryTreeNode* node) {
    if (node == nullptr) return;
    postorderTraversal(node->left); // 先遍历左子树
    postorderTraversal(node->right); // 再遍历右子树
    cout << node->value << " "; // 最后访问根节点
}

int main() {
    // 创建二叉树示例
    BinaryTreeNode* root = new BinaryTreeNode(1);
    root->left = new BinaryTreeNode(2);
    root->right = new BinaryTreeNode(3);
    root->left->left = new BinaryTreeNode(4);
    root->left->right = new BinaryTreeNode(5);

    // 前序遍历
    cout << "前序遍历结果：" << endl;
    preorderTraversal(root);
    cout << endl;

    // 中序遍历
    cout << "中序遍历结果：" << endl;
    inorderTraversal(root);
    cout << endl;

    // 后序遍历
    cout << "后序遍历结果：" << endl;
    postorderTraversal(root);
    cout << endl;

    // 释放内存
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

线索二叉树是一种特殊的二叉树，它在每个节点中保存了指向其前驱和后继节点的指针。这样可以方便地实现中序遍历，并且节省了空间。

对于每个节点，线索二叉树可以设置两种类型的线索：

1. 前驱线索（predecessor thread）：指向该节点在中序遍历序列中的前驱节点。
2. 后继线索（successor thread）：指向该节点在中序遍历序列中的后继节点。

线索二叉树的特点包括：

• 线索化后，对于任意节点，其左子节点指针如果为空，则指向其前驱节点；其右子节点指针如果为空，则指向其后继节点。
• 线索化后，可以通过节点的前驱和后继指针，实现高效的中序遍历，而无需使用递归或栈来维护遍历路径。

以下是如何实现线索二叉树以及通过前驱和后继指针进行中序遍历的c++代码

#include <iostream>

using namespace std;

// 二叉树节点类
class BinaryTreeNode {
public:
    int value;
    BinaryTreeNode* left;
    BinaryTreeNode* right;
    bool isThreaded; // 是否线索化
    BinaryTreeNode* pre; // 前驱节点指针

    // 构造函数
    BinaryTreeNode(int val) : value(val), left(nullptr), right(nullptr), isThreaded(false), pre(nullptr) {}
};

// 线索化二叉树
void threadedBinaryTree(BinaryTreeNode* root, BinaryTreeNode*& pre) {
    if (root == nullptr) return;
    
    // 线索化左子树
    threadedBinaryTree(root->left, pre);
    
    // 当前节点的前驱线索指向前一个节点
    if (root->left == nullptr) {
        root->left = pre;
        root->isThreaded = true;
    }
    
    // 前一个节点的后继线索指向当前节点
    if (pre != nullptr && pre->right == nullptr) {
        pre->right = root;
        pre->isThreaded = true;
    }
    
    // 更新前一个节点为当前节点
    pre = root;
    
    // 线索化右子树
    threadedBinaryTree(root->right, pre);
}

// 中序遍历线索二叉树
void threadedInorderTraversal(BinaryTreeNode* root) {
    BinaryTreeNode* current = root;
    while (current != nullptr) {
        while (current->left != nullptr && !current->isThreaded) {
            current = current->left;
        }
        cout << current->value << " ";
        
        if (current->right != nullptr && !current->right->isThreaded) {
            current = current->right;
        } else {
            current = current->right;
            while (current != nullptr && current->isThreaded) {
                cout << current->value << " ";
                current = current->right;
            }
        }
    }
}

int main() {
    // 创建线索二叉树示例
    BinaryTreeNode* root = new BinaryTreeNode(1);
    root->left = new BinaryTreeNode(2);
    root->right = new BinaryTreeNode(3);
    root->left->left = new BinaryTreeNode(4);
    root->left->right = new BinaryTreeNode(5);

    // 线索化二叉树
    BinaryTreeNode* pre = nullptr;
    threadedBinaryTree(root, pre);

    // 中序遍历线索二叉树
    cout << "中序遍历结果：" << endl;
    threadedInorderTraversal(root);
    cout << endl;

    // 释放内存
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

 四.树和森林

        树和森林是计算机科学中常见的数据结构，它们之间有着密切的联系。

        树是一种非线性的数据结构，由节点和边组成，每个节点最多有一个父节点和零个或多个子节点。树中的节点之间存在唯一的路径。树具有层级结构，最顶层的节点称为根节点，没有父节点的节点称为叶节点。在树中，任意节点都可以作为其他节点的父节点，因此树提供了一种自然的层次结构，常用于表示具有层次关系的数据。

        森林是由多棵互不相交的树组成的集合。换言之，森林是多个树的集合，其中每棵树都是独立的，彼此之间没有交集。森林的概念来源于自然界中的森林，其中每棵树都是独立的生长，相互之间不干扰。

        在计算机科学中，森林常用于表示多个独立的数据结构，每个数据结构都可以看作是一棵树。例如，森林可以用于表示多个文件系统中的目录结构，每个目录结构都是一棵树，而多个目录结构的集合则构成了一个森林。

以下是如何实现树和森林的代码

#include <iostream>
#include <vector>

using namespace std;

// 树节点类
class TreeNode {
public:
    int value;
    vector<TreeNode*> children;

    // 构造函数
    TreeNode(int val) : value(val) {}
};

// 树类
class Tree {
public:
    TreeNode* root;

    // 构造函数
    Tree() : root(nullptr) {}

    // 插入节点
    void insert(int parentVal, int childVal) {
        TreeNode* newNode = new TreeNode(childVal);
        if (root == nullptr) {
            root = newNode;
            return;
        }
        insertNode(root, parentVal, newNode);
    }

    // 插入节点的辅助函数
    void insertNode(TreeNode* node, int parentVal, TreeNode* newNode) {
        if (node->value == parentVal) {
            node->children.push_back(newNode);
            return;
        }
        for (TreeNode* child : node->children) {
            insertNode(child, parentVal, newNode);
        }
    }
};

// 森林类
class Forest {
public:
    vector<Tree*> trees;

    // 添加树
    void addTree(Tree* tree) {
        trees.push_back(tree);
    }
};

int main() {
    // 创建树和森林示例
    Tree tree1, tree2;
    tree1.insert(1, 2);
    tree1.insert(1, 3);
    tree1.insert(2, 4);
    tree2.insert(5, 6);
    tree2.insert(5, 7);
    
    Forest forest;
    forest.addTree(&tree1);
    forest.addTree(&tree2);

    // 输出树和森林的结构
    cout << "树1的结构：" << endl;
    cout << "  1" << endl;
    cout << " / \\" << endl;
    cout << "2   3" << endl;
    cout << "|" << endl;
    cout << "4" << endl;
    
    cout << "树2的结构：" << endl;
    cout << "  5" << endl;
    cout << " / \\" << endl;
    cout << "6   7" << endl;

    return 0;
}

五.树与二叉树的应用

树和二叉树在计算机科学中有广泛的应用，包括：

• 数据库索引：使用B树和B+树来加速数据库查询。
• 编译器设计：使用语法树来表示程序的结构。
• 文件系统：使用文件系统树来组织文件和目录。
• 图形用户界面：使用树来表示窗口和控件的层次结构。
• 人工智能：使用决策树来进行分类和预测。

例如，以下是一个运用B+树加速数据库查询的过程

#include <iostream>
#include <vector>

using namespace std;

// B+树节点类
class BPlusTreeNode {
public:
    vector<int> keys; // 节点的关键字
    vector<BPlusTreeNode*> children; // 子节点指针

    // 构造函数
    BPlusTreeNode() {}

    // 判断节点是否为叶子节点
    bool isLeaf() {
        return children.empty();
    }
};

// B+树类
class BPlusTree {
public:
    BPlusTreeNode* root;

    // 构造函数
    BPlusTree() : root(nullptr) {}

    // 插入关键字
    void insert(int key) {
        if (root == nullptr) {
            root = new BPlusTreeNode();
            root->keys.push_back(key);
            return;
        }
        insertNode(root, key);
    }

    // 插入关键字的辅助函数
    void insertNode(BPlusTreeNode* node, int key) {
        if (node->isLeaf()) {
            // 叶子节点直接插入
            auto it = lower_bound(node->keys.begin(), node->keys.end(), key);
            node->keys.insert(it, key);
            return;
        }
        // 非叶子节点找到合适的子节点递归插入
        int i = 0;
        while (i < node->keys.size() && key > node->keys[i]) {
            i++;
        }
        insertNode(node->children[i], key);
    }
};

int main() {
    // 创建B+树示例
    BPlusTree bPlusTree;
    bPlusTree.insert(10);
    bPlusTree.insert(5);
    bPlusTree.insert(20);
    bPlusTree.insert(3);
    bPlusTree.insert(8);
    bPlusTree.insert(15);
    bPlusTree.insert(25);

    // 输出B+树结构
    cout << "B+树结构：" << endl;
    cout << "Root -> ";
    for (int key : bPlusTree.root->keys) {
        cout << key << " ";
    }
    cout << endl;

    return 0;
}

六.实际案例

        假设我们要设计一个文件系统，需要组织文件和目录的层次结构。这个问题可以用树来解决。每个目录可以看作是一个节点，它可以包含其他目录（子节点）或文件（叶节点）。这样，我们就可以使用树来表示文件系统的结构，并且方便地进行文件的查找和操作。

代码如下：

#include <iostream>
#include <string>
#include <vector>

using namespace std;

class Node {
public:
    string name;
    vector<Node*> children;

    Node(string n) : name(n) {}
};

class FileSystem {
public:
    Node* root;

    FileSystem(string rootName) {
        root = new Node(rootName);
    }

    void addFile(string path, string fileName) {
        Node* current = root;
        vector<string> directories = split(path, '/');

        for (string dir : directories) {
            bool found = false;
            for (Node* child : current->children) {
                if (child->name == dir) {
                    current = child;
                    found = true;
                    break;
                }
            }
            if (!found) {
                Node* newDir = new Node(dir);
                current->children.push_back(newDir);
                current = newDir;
            }
        }

        current->children.push_back(new Node(fileName));
    }

    void printFileSystem() {
        printFiles(root, 0);
    }

private:
    void printFiles(Node* node, int level) {
        for (int i = 0; i < level; i++) {
            cout << "  ";
        }
        cout << node->name << endl;

        for (Node* child : node->children) {
            printFiles(child, level + 1);
        }
    }

    vector<string> split(string str, char delimiter) {
        vector<string> result;
        stringstream ss(str);
        string token;

        while (getline(ss, token, delimiter)) {
            result.push_back(token);
        }

        return result;
    }
};

int main() {
    FileSystem fs("root");
    fs.addFile("/dir1/file1", "file1");
    fs.addFile("/dir1/dir2/file2", "file2");
    fs.addFile("/dir1/dir2/dir3/file3", "file3");
    fs.printFileSystem();

    return 0;
}

        在这个示例中，我们定义了一个Node类来表示文件系统中的每个节点。每个节点都有一个名称和一个子节点列表。FileSystem类表示整个文件系统，它有一个根节点。

        addFile函数用于向文件系统中添加文件。它接受一个路径和一个文件名作为参数。它会沿着路径创建目录，并在最后一个目录中添加文件。

        printFileSystem函数用于打印文件系统的结构。它使用递归来遍历树，并打印每个节点的名称。

七.总结

        树和二叉树是非常重要的数据结构，它们在计算机科学中有广泛的应用。树的结构类似于自然界中的树，而二叉树是一种特殊的树，它的每个节点最多有两个子节点。

        遍历是访问二叉树中所有节点的重要操作，常见的遍历方式有前序遍历、中序遍历和后序遍历。

        线索二叉树是一种特殊的二叉树，它在每个节点中保存了指向其前驱和后继节点的指针。

        树和森林是相关的概念，森林是由多棵互不相交的树组成的集合。树和二叉树在数据库索引、编译器设计、文件系统、图形用户界面和人工智能等方面都有广泛的应用。文章来源地址https://www.toymoban.com/news/detail-859784.html

到了这里，关于探索树与二叉树：从基础到应用的完整指南的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！