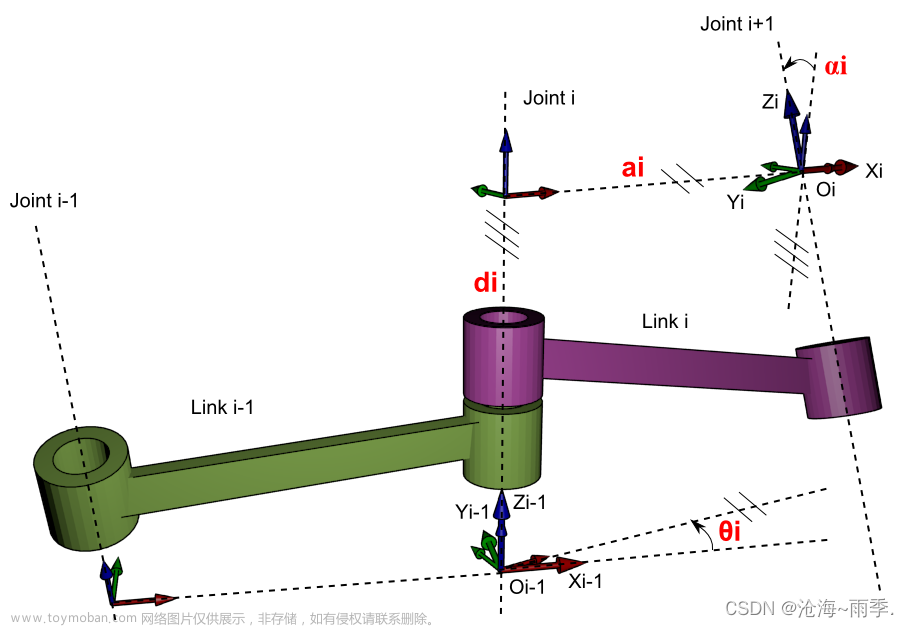
一、雅可比矩阵介绍
雅可比矩阵：机器人操作空间速度与关节空间速度的线性映射关系，可以视作从关节空间向操作空间运动速度的传动比。
令机械手的运动方程为： 表示操作空间与关节空间的位移关系
则两边同时对时间求导，就可以求解出q与x之间的微分关系
,其中J(q)是6*n的偏导数矩阵。表示机械手的雅可比矩阵。
由于刚体坐标系的广义速度由线速度和角速度组成，即
。则其中J（q）的上三行表示对夹手线速度的传递比，下三行表示对夹手角速度的传递比。而每一列表示对相应的关节速度对于夹手线速度和角速度的传递比，具体如下：
则，相应的夹手线速度和角速度可以表示为各关节速度的线性函数如下：
二、矢量积法计算雅可比矩阵
根据关节速度的传递情况，末端夹手的线速度和角速度与某一关节速度存在一定的关系，具体传递情况分析如下：
1.对于移动关节，关节变量只引起末端夹手线速度的变化，其映射关系为：
其中，Xi表示关节变量qi对应的移动轴。
2.对于转动关节，关节变量步进引起末端线速度变化还引起了角速度变化，其映射关系为：
其中，
表示关节变量qi对应的转动轴在基系下的表达。
表示夹手坐标原点相对于坐标系{i-1}的位置矢量在基座标系中的表达。
则相应的雅可比矩阵的第i列可以表示为：
通过上述关系即可以获得相应的雅可比矩阵。文章来源：https://www.toymoban.com/news/detail-859916.html
本文参考《机器人学》第三版 蔡自兴、谢斌编著。文章来源地址https://www.toymoban.com/news/detail-859916.html
到了这里，关于机器人逆运动学求解——矢量积法计算雅可比矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
