C++ 动态规划 01背包问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了C++ 动态规划 01背包问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

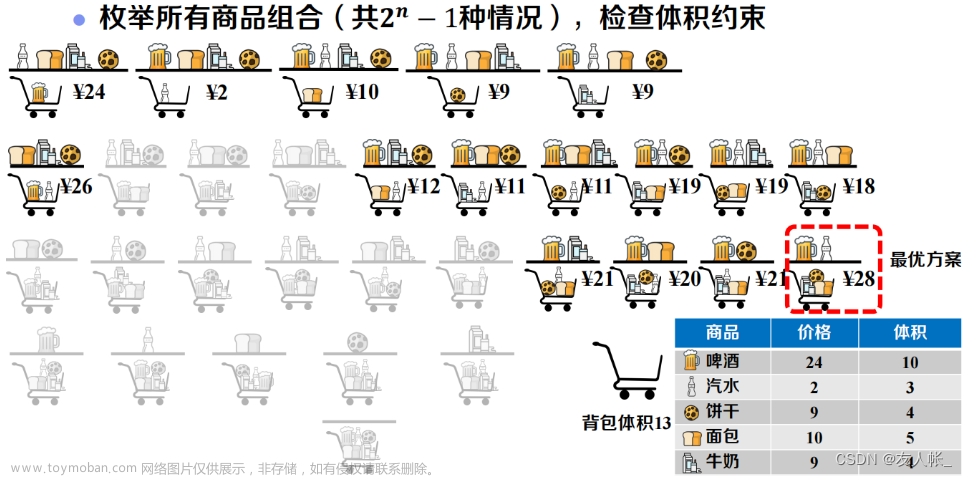
有 N
件物品和一个容量是 V
的背包。每件物品只能使用一次。

第 i
件物品的体积是 vi
，价值是 wi
。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数， N，V
，用空格隔开，分别表示物品数量和背包容积。

接下来有 N
行，每行两个整数 vi,wi
，用空格隔开，分别表示第 i
件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000

0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8
c++01背包问题,力扣,动态规划,算法笔记,动态规划,c++,算法

这是一个经典的动态规划问题，称为"01背包问题"。问题描述如下：

有一个容量为 m 的背包，和 n 个物品，每个物品有两个属性：体积 v[i] 和价值 w[i]。要求选择一些物品放入背包中，使得放入的物品的体积总和不超过背包容量，且价值最大。

这里的 f[i][j] 表示前 i 个物品放入容量为 j 的背包中的最大价值。状态转移方程为：

f[i][j]=max⁡(f[i−1][j],f[i−1][j−v[i]]+w[i])f[i][j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i])

其中，第一项 f[i−1][j]f[i−1][j] 表示不选择第 i 个物品，第二项 f[i−1][j−v[i]]+w[i]f[i−1][j−v[i]]+w[i] 表示选择第 i 个物品。选择的条件是当前背包容量 j 大于等于第 i 个物品的体积 v[i]。

最终的答案即为 f[n][m]，表示前 n 个物品放入容量为 m 的背包中的最大价值。

这个问题的动态规划思路是从前往后逐个决策，通过填表的方式记录状态转移，最终求得问题的最优解。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main ()
{
    cin>>n>>m;
    
    for(int i = 1; i <= n; i ++ ) cin>>v[i]>>w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    
    cout<<f[n][m]<<endl;
    
    return 0;
}

楼主刚接触DP感觉很抽象，这里加些输出，辅助理解一下过程就清晰多了。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];


void out(int x, int y)
{
    cout<<"i = "<<x<<"; j = "<<y<<";"<<endl;
    for(int i = 0; i <= n; i ++ )
    {
        for(int j = 0; j <= m; j ++ )
        {
            cout<<f[i][j]<<" ";
        }
        cout<<endl;
    }
}

int main ()
{
    cin>>n>>m;

    for(int i = 1; i <= n; i ++ ) cin>>v[i]>>w[i];
    out(11, 22);
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
        {
            cout<<"1"<<endl;
            f[i][j] = f[i - 1][j];
            out(i, j);
            cout<<"2"<<endl;
            cout<<"v[i] = "<<v[i]<<endl;
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            out(i, j);
        }

    cout<<f[n][m]<<endl;

    return 0;
}

下面是样例的输出：

4 5
1 2
2 4
3 4
4 5
i = 11; j = 22;
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 1; j = 0;
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 1
i = 1; j = 0;
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 1; j = 1;
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 1
i = 1; j = 1;
0 0 0 0 0 0
0 2 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 1; j = 2;
0 0 0 0 0 0
0 2 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 1
i = 1; j = 2;
0 0 0 0 0 0
0 2 2 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 1; j = 3;
0 0 0 0 0 0
0 2 2 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 1
i = 1; j = 3;
0 0 0 0 0 0
0 2 2 2 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 1; j = 4;
0 0 0 0 0 0
0 2 2 2 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 1
i = 1; j = 4;
0 0 0 0 0 0
0 2 2 2 2 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 1; j = 5;
0 0 0 0 0 0
0 2 2 2 2 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 1
i = 1; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 2; j = 0;
0 0 0 0 0 0
0 2 2 2 2 2
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 2
i = 2; j = 0;
0 0 0 0 0 0
0 2 2 2 2 2
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 2; j = 1;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 2
i = 2; j = 1;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 2; j = 2;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 2 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 2
i = 2; j = 2;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 2; j = 3;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 2 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 2
i = 2; j = 3;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 2; j = 4;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 2 0
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 2
i = 2; j = 4;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 0
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 2; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 2
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 2
i = 2; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 3; j = 0;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 0 0 0 0 0
0 0 0 0 0 0
2
v[i] = 3
i = 3; j = 0;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 0 0 0 0 0
0 0 0 0 0 0
1
i = 3; j = 1;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 0 0 0 0
0 0 0 0 0 0
2
v[i] = 3
i = 3; j = 1;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 0 0 0 0
0 0 0 0 0 0
1
i = 3; j = 2;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 0 0 0
0 0 0 0 0 0
2
v[i] = 3
i = 3; j = 2;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 0 0 0
0 0 0 0 0 0
1
i = 3; j = 3;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 0 0
0 0 0 0 0 0
2
v[i] = 3
i = 3; j = 3;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 0 0
0 0 0 0 0 0
1
i = 3; j = 4;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 0
0 0 0 0 0 0
2
v[i] = 3
i = 3; j = 4;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 0
0 0 0 0 0 0
1
i = 3; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 6
0 0 0 0 0 0
2
v[i] = 3
i = 3; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 0 0 0 0 0
1
i = 4; j = 0;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 0 0 0 0 0
2
v[i] = 4
i = 4; j = 0;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 0 0 0 0 0
1
i = 4; j = 1;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 0 0 0 0
2
v[i] = 4
i = 4; j = 1;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 0 0 0 0
1
i = 4; j = 2;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 0 0 0
2
v[i] = 4
i = 4; j = 2;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 0 0 0
1
i = 4; j = 3;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 6 0 0
2
v[i] = 4
i = 4; j = 3;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 6 0 0
1
i = 4; j = 4;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 6 6 0
2
v[i] = 4
i = 4; j = 4;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 6 6 0
1
i = 4; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 6 6 8
2
v[i] = 4
i = 4; j = 5;
0 0 0 0 0 0
0 2 2 2 2 2
0 2 4 6 6 6
0 2 4 6 6 8
0 2 4 6 6 8
8

Process returned 0 (0x0)   execution time : 9.800 s
Press any key to continue.

下面的代码是优化成一维数组的代码：
当解决01背包问题时，我们使用二维数组f[i][j]表示前i个物品在背包容量为j时的最大价值。在动态规划的过程中，每次计算f[i][j]时，只需要用到上一行f[i-1][k]的信息（其中0 <= k <= j）。

考虑优化空间，我们可以使用一维数组f[j]表示在背包容量为j时的最大价值，同时逐步迭代更新这个一维数组。在每一轮外层循环中，我们通过反向遍历背包容量j，更新f[j]的值。这样，在更新f[j]的过程中，我们相当于使用了上一轮循环中的f[j-v[i]]，这就达到了压缩状态的效果。

让我们详细解释这个代码：

f[j]数组的含义：f[j]表示背包容量为j时的最大价值。

外层循环 for(int i = 1; i <= n; i++) 遍历每个物品。

内层循环 for(int j = m; j >= v[i]; j--) 从背包容量m开始向前遍历，确保在更新f[j]时使用的是上一轮循环中的f[j-v[i]]。

状态转移方程：f[j] = max(f[j], f[j - v[i]] + w[i])，表示考虑是否放入第i个物品，如果放入，则更新背包容量为j时的最大价值。

最终结果为 cout << f[m] << endl;，表示在背包容量为m时的最大价值。

这种状态压缩的思想在动态规划中常被使用，通过适当的设计状态转移方程和遍历顺序，可以在保证算法正确性的前提下减少空间复杂度。文章来源地址https://www.toymoban.com/news/detail-859918.html

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main ()
{
    cin>>n>>m;
    
    for(int i = 1; i <= n; i ++ ) cin>>v[i]>>w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = m; j >= v[i]; j -- )
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    
    cout<<f[m]<<endl;
    
    return 0;
}