动态规划——路径问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划——路径问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

什么是路径问题？

练习

练习1：不同路径

练习2：不同路径II

练习3：珠宝的最高价值

练习4：下降路径最小和

练习5：地下城游戏

什么是路径问题？

动态规划中的路径问题：指在一个给定的网格中，从起点到终点有多条可能的路径，每条路径都有一个特定的权重或成本，动态规划路径问题的目标是找到一条路径使得其总权重或成本最小或最大化。

在解决这类问题时，通常会使用动态规划算法，通过逐步计算子问题的最优解来找到整体问题的最优解。

关于动态规划的解题过程，可参考：

接下来，我们通过一些练习来进一步体会路径问题及其解决方法

练习

练习1：不同路径

题目链接：

62. 不同路径 - 力扣（LeetCode）

题目描述：

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109

思路分析：

要求从网格的左上方走到网格的右下方一共有多少条路径，且一次只能向右或向下移动一步

我们先来分析状态表示：

我们以 [i, j]位置为结尾进行分析：

那么在本题中，以[i, j]位置为结尾，则可表示为到达[i, j]位置

则dp[i][j]则可表示：到达[i, j]位置时的总路径数

状态转移方程：

由于一次只能向右或向下移动一步，因此，只能从[i-1, j] 或 [i, j-1]位置到达 [i, j]位置

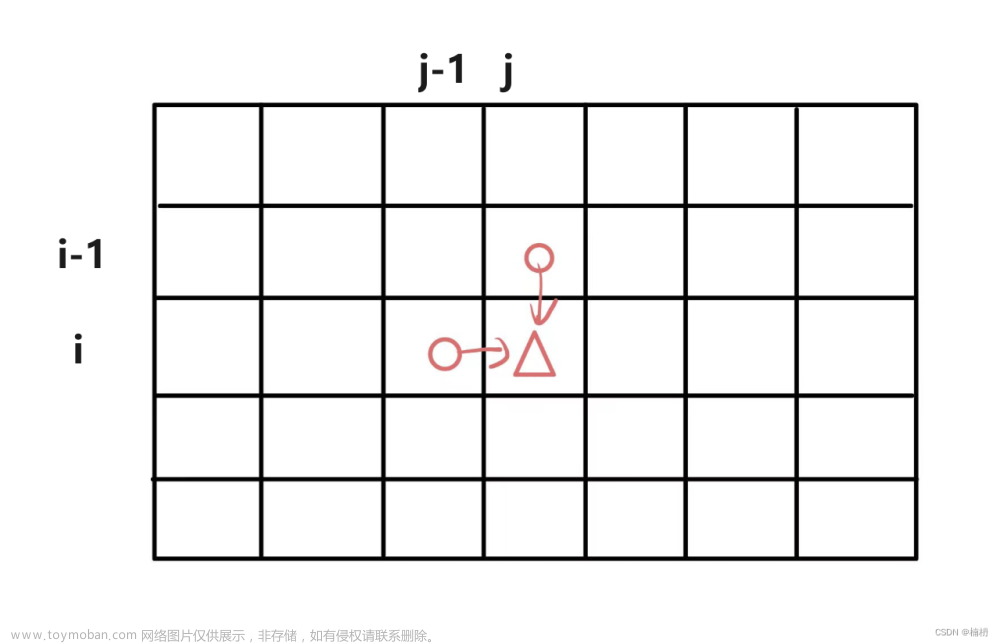
动态规划路径,Java刷题,动态规划,算法,java,leetcode

由于 dp[i][j]表示到达[i, j]位置时的总路径数，因此，

dp[i-1][j]：到达[i-1, j]位置的总路径数，从[i-1, j]向下走一步，可到达[i, j]位置，因此，从[i-1, j]位置到达[i, j]的总路径数为 dp[i-1][j]

同理，从[i, j-1]向右走一步可到达[i, j]位置，从[i, j-1]位置到达[i, j]的总路径数为dp[i][j-1]

可得：到达[i, j]位置的总路径数 dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始化：

由于 dp[i][j] = dp[i-1][j] + dp[i][j-1]，当i = 0 或 j = 0时，填表就会越界，我们可以选择先初始化这些位置的值，也可以通过 添加辅助节点 的方式来帮助我们进行初始化和填表：

我们在最上面添加一行，方便原 i = 0 位置的元素进行初始化，在最左边添加一列，方便原j = 0位置的元素进行初始化

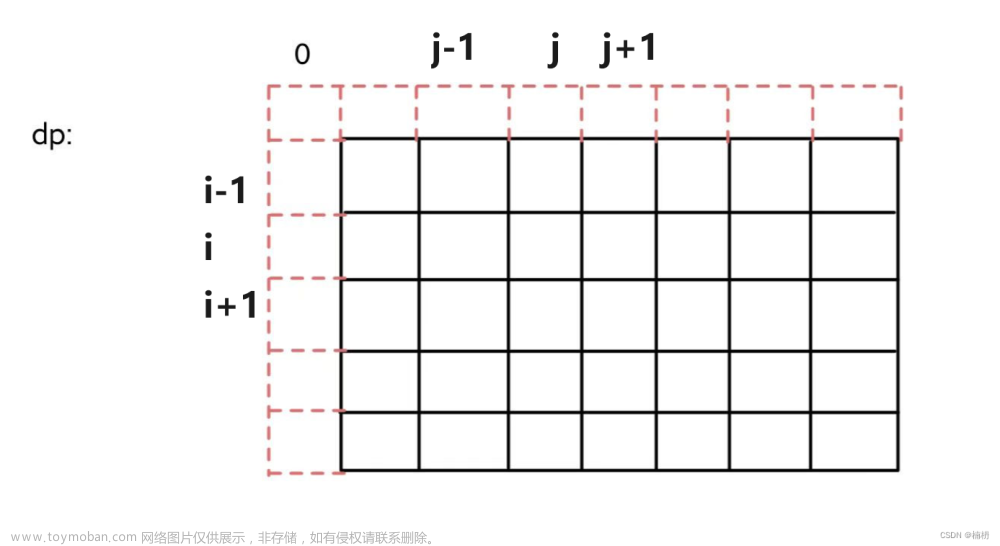
动态规划路径,Java刷题,动态规划,算法,java,leetcode

添加辅助节点后，我们要考虑：

（1）辅助节点里的值要保证后续填表过程中不出错

原 i = 0 的所有位置只能由左侧([i, j-1])向右移动而来，不能从[i-1,j]移动而来，因此，其总路径数 = dp[i][j-1]，即 dp[i-1][j] = 0，将最上面添加的辅助节点初始化为 0

同理，原 j = 0 的所有位置只能由上侧([i-1, j])向下移动而来，dp[i][j-1] = 0，将最左侧添加的辅助节点初始化为 0

但注意：要从起始位置开始移动，因此起始位置要置为 1，起始位置可从上面向下移动而来，也可由左面向右移动而来，因此可将 dp[0][1] （或dp[1][0]）置为1

（2）下标的映射关系

题目中只给出该网格是一个 m * n的表格，要求我们找到从左上角到右下角的所有路径数，因此，我们以 [1, 1]为新的起始位置，[m, n]为结束位置

填表顺序：

由于 dp[i][j] = dp[i-1][j] + dp[i][j-1]，我们在填写[i, j]位置的值时，要先确定[i-1, j]和 [i, j-1]位置的值，因此，我们以从上到下，且每一行从左到右的顺序进行填表

返回值：

题目要求我们返回从左上角到右下角的所有路径，即到达[m, n]位置时的所有路径，因此返回dp[m][n]

代码实现：

class Solution {
    public int uniquePaths(int m, int n) {
      //创建dp表
      int[][] dp = new int[m+1][n+1];
      //初始化
      dp[0][1] = 1;
      //填表
      for(int i = 1; i <= m; i++){
        for(int j = 1; j <= n; j++){
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
      }
      //返回
      return dp[m][n];
    }
}

练习2：不同路径II

题目链接：

63. 不同路径 II - 力扣（LeetCode）

题目描述：

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

思路分析：

本题与 练习1：不同路径 类似，同样是求从左上角到右下角的所有路径数，但本题的网格中存在障碍物，当遇到障碍物时，不能通过

状态表示：

我们以 [i, j]位置为结尾进行分析：

则dp[i][j]则可表示：到达[i, j]位置时的总路径数

状态转移方程：

由于本题中存在障碍物，因此，

（1）若当前位置 obstacleGrid[i][j] 为 1，则当前位置不可通过，不能由该位置向右或向下移动，即 dp[i][j] = 0；

（2）若当前位置 obstacleGrid[i][j] 为 1，则当前位置可通过，可由该位置继续向右或向下移动，由于一次只能向右或向下移动一步，因此，只能从[i-1, j] 或 [i, j-1]位置到达 [i, j]位置

由于 dp[i][j]表示到达[i, j]位置时的总路径数，因此，

dp[i-1][j]：到达[i-1, j]位置的总路径数，从[i-1, j]向下走一步，可到达[i, j]位置，因此，从[i-1, j]位置到达[i, j]的总路径数为 dp[i-1][j]

同理，从[i, j-1]向右走一步可到达[i, j]位置，从[i, j-1]位置到达[i, j]的总路径数为dp[i][j-1]

则到达[i, j]位置的总路径数 dp[i][j] = dp[i-1][j] + dp[i][j-1]

因此 若 obstacleGrid[i][j] = 1，dp[i][j] = 0；若 obstacleGrid[i][j] = 0，dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始化：

当i = 0 或 j = 0时，会越界，我们可以选择先初始化这些位置的值，也可以通过添加辅助节点的方式来帮助我们进行初始化和填表：

我们在最上面添加一行，方便原 i = 0 位置的元素进行初始化，在最左边添加一列，方便原j = 0位置的元素进行初始化

动态规划路径,Java刷题,动态规划,算法,java,leetcode

在添加辅助节点后，我们要考虑：

（1）辅助节点里的值要保证后续填表过程中不出错

同理，原 j = 0 的所有位置只能由上侧([i-1, j])向下移动而来，dp[i][j-1] = 0，将最左侧添加的辅助节点初始化为 0

但注意：要从起始位置开始移动，因此要置为 1，起始位置可从上面向下移动而来，也可由左面向右移动而来，因此可将 dp[0][1] （或dp[1][0]）置为1

（2）下标的映射关系

在添加辅助节点后，dp[i][j]位置对应 obstacleGrid[i-1][j-1]位置

填表顺序：从上到下，且每一行从左到右

返回值：dp[m][n]

代码实现：

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        //创建dp表
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m+1][n+1];
        //初始化
        dp[0][1] = 1;
        //填表
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(obstacleGrid[i-1][j-1] == 1) dp[i][j] = 0;
                else dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        //返回
        return dp[m][n];
    }
}

练习3：珠宝的最高价值

题目链接：

LCR 166. 珠宝的最高价值 - 力扣（LeetCode）

题目描述：

现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为：

只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时，停止拿取

注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。

示例 1:

输入: frame = [[1,3,1],[1,5,1],[4,2,1]]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最高价值的珠宝

提示：

0 < frame.length <= 200
0 < frame[0].length <= 200

思路分析：

题目要求我们从左上角开始拿珠宝，拿到当前位置的珠宝（frame[i][j]）后，可向右或向下移动一格，直到移动到右下角

状态表示：

我们以 [i, j]位置为结尾进行分析：

则dp[i][j]则可表示：到达[i, j]位置时，获得的珠宝最高价值为 dp[i]][j]

状态转移方程：

由于一次只能向右或向下移动一步，因此，只能从[i-1, j] 或 [i, j-1]位置到达 [i, j]位置

由于 dp[i][j]表示到达[i, j]位置时获得的珠宝最高价值，因此，

dp[i-1][j]：到达[i-1, j]位置，从[i-1, j]向下走一步，可到达[i, j]位置，因此，从[i-1, j]位置到达[i, j]的珠宝最高价值为 dp[i-1][j] + frame[i][j]

同理，从[i, j-1]向右走一步可到达[i, j]位置，从[i, j-1]位置到达[i, j]的珠宝最高价值为dp[i][j-1] + frame[i][j]

可得：到达[i, j]位置时的珠宝最高价值 dp[i][j] = max(dp[i-1][j] , dp[i, j-1]) + frame[i][j]

初始化：

同样的，当 i = 0 或 j = 0时，填表会越界，因此，我们可以通过添加辅助节点的方式来帮助我们进行初始化和填表：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

（1）辅助节点里的值要保证后续填表过程中不出错

原 i = 0 的所有位置只能由左侧([i-1, j])向右移动而来，不能从[i,j-1]移动而来，因此，珠宝的最高价值 = dp[i-1][j]，所有 dp[i][j-1] = 0，将最上面添加的辅助节点初始化为 0

同理，原 j = 0 的所有位置只能由上侧([i, j-1])向下移动而来，dp[i-1][j] = 0，将最左侧添加的辅助节点初始化为 0

（2）下标的映射关系

在添加辅助节点后，dp[i][j]位置对应 frame[i-1][j-1]位置

填表顺序：从上到下，且每一行从左到右

返回值：dp[m][n]

代码实现：

class Solution {
    public int jewelleryValue(int[][] frame) {
        //创建dp表
        int m = frame.length;
        int n = frame[0].length;
        int[][] dp = new int[m+1][n+1];
        //初始化
        //填表
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]) + frame[i-1][j-1];
            }
        }
        //返回
        return dp[m][n];

    }
}

练习4：下降路径最小和

题目链接：

931. 下降路径最小和 - 力扣（LeetCode）

题目描述：

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

思路分析：

我们首先来分析题目要求：

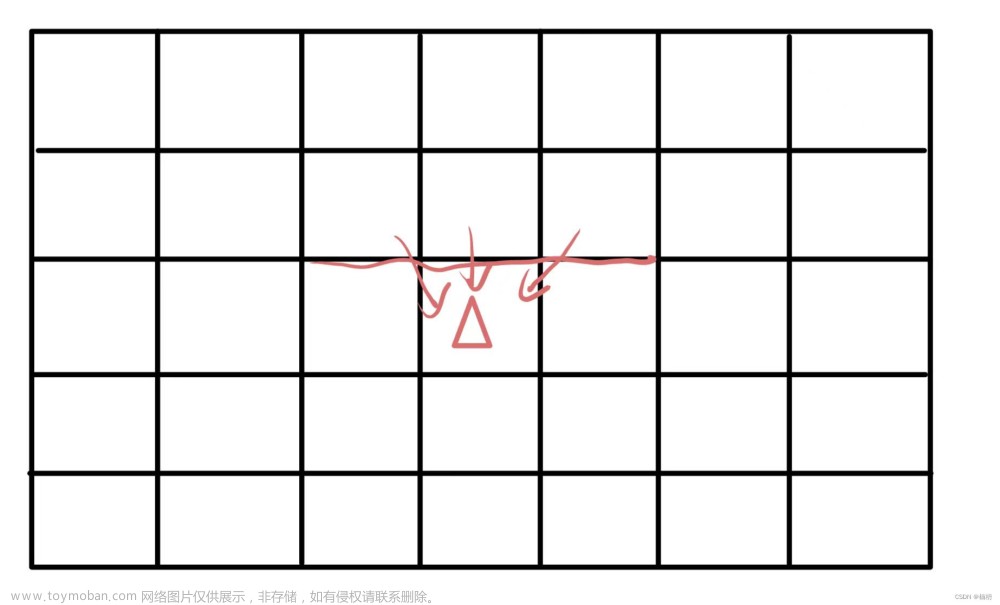
当我们从一行中选择一个元素（matrix[i][j]）后，可在下一行选择和当前行所选元素最多相隔一列（matrix[i-1][j+1] matrix[i][j+1] matrix[i+1][j]），要得到下降路径的最小和，因此，要在这三个元素中选择最小的一个

状态表示：

我们以[i, j]位置为结尾进行分析：

以[i, j]位置为结尾，可表示下降至[i, j]位置

则 dp[i, j]可表示：下降到dp[i, j]位置时的路径最小和

状态转移方程：

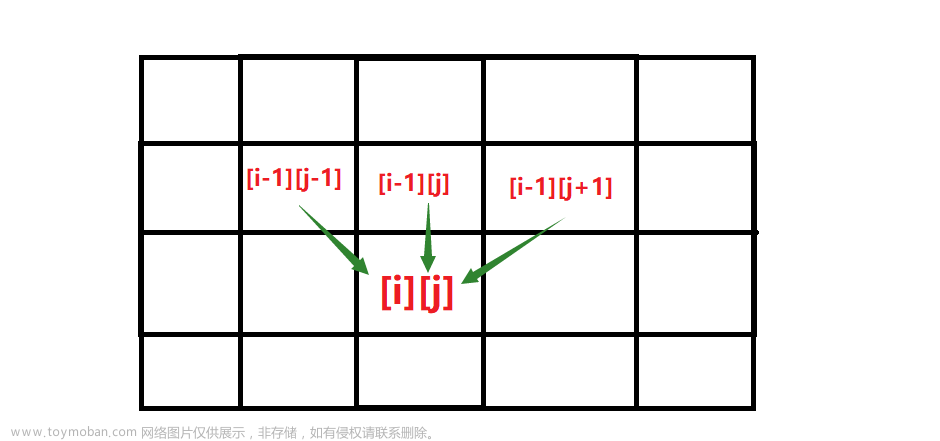
下降至[i, j]位置后，可下降至[i-1, j+1]、[i, j+1]和 [i+1,j+1]位置，因此，到达[i, j]位置，可由[i-1, j-1]、[i, j-1] 和 [i+1, j-1]位置下落

动态规划路径,Java刷题,动态规划,算法,java,leetcode

dp[i][j]：下降至[i, j]位置时的最小路径和，因此dp[i-1][j -1]表示下降到[i-1, j-1]位置时的最小路径和，从[i-1, j-1]位置下降至[i, j]位置，最小路径和为：dp[i-1][ j-1] + matrix[i][j]

同理，从[i, j-1]位置下降至[i, j]位置的最小路径和为：dp[i][j-1] + matrix[i][j]

从[i+1, j-1]位置下降至[i, j]位置的最小路径和为：dp[i+1][j-1] + matrix[i][j]

因此，要得求到达[i, j]位置的最小路径和，只需求出[i-1, j-1]、[i, j-1] 和 [i+1, j-1]中的最小路径和，再 + maxtrix[i][j]即可

dp[i][j] = min(dp[i-1][j-1], dp[i, j-1], dp[i+1][j-1]) + matrix[i][j]

初始化：

由于dp[i][j] = min(dp[i-1][j-1], dp[i, j-1], dp[i+1][j-1]) + matrix[i][j] ，因此在求第一列和最后一列的最小路径和时，可能会出错

动态规划路径,Java刷题,动态规划,算法,java,leetcode

在这里，我们仍采用添加辅助节点的方式来进行帮助我们进行初始化和填表：

我们在第一行的最上面、第一列的前面和最后一列的后面分别添加一列：

这样，我们就无需再处理原来的边界情况，在添加辅助节点时要注意：

1. 辅助节点里的值要保证后续填表过程中不出错

虽然添加辅助节点后，我们无需再处理原来的边界情况，但是，由于辅助节点是不存在的，因此，不能由辅助节点下落，即不能取辅助节点中的值

如何初始化才能让辅助节点中的值不影响后续填表？

dp[i][j] = min(dp[i-1][j-1], dp[i, j-1], dp[i+1][j-1]) + matrix[i][j] ，我们需要在取其中的最小值，要保证在任何情况下都不会取辅助节点中的值，我们可以将辅助节点中的值初始化为最大值（-100 <= matrix[i][j] <= 100，最大值只需大于100即可），这样，就能够保证不取到辅助节点中的值

2. 下标的映射关系

在添加辅助节点后，matrix和dp表的映射关系发生变化：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

dp[i][j]对应matrix[i-1][j-1]

填表顺序：从上到下，每一行从左到右

返回值：要求下降到最后一行的路径最小和，因此，需要返回最后一行的最小值

代码实现：

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        //创建dp表
        int[][] dp = new int[n+1][n+2];
        //初始化
        for(int i = 1; i <= n; i++){
            dp[i][0] = Integer.MAX_VALUE;
            dp[i][n+1] = Integer.MAX_VALUE;
        }
        //填表
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <=n; j++){
                dp[i][j] = Math.min(Math.min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + matrix[i-1][j-1];
            }
        }
        //返回
        int min = dp[n][1];
        for(int i = 2; i <= n; i++){
            min = Math.min(dp[n][i], min);
        }
        return min;
    }
}

练习5：地下城游戏

题目链接：

174. 地下城游戏 - 力扣（LeetCode）

题目描述：

174. 地下城游戏

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只向右或向下移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

示例 2：

输入：dungeon = [[0]]
输出：1

提示：

m == dungeon.length
n == dungeon[i].length
1 <= m, n <= 200
-1000 <= dungeon[i][j] <= 1000

思路分析：

骑士要从左上角起始位置到达右下角最终位置救公主，每个位置中有一个健康点数（dungeon[i][j]），为负时，骑士失去健康点数；为正时，增加健康点数。当健康点数 <= 0时，骑士死亡，因此，我们要保证骑士到达右下角时至少有 1 点健康点数，且中途健康点数不能低于1

我们首先分析状态表示：

我们以[i, j] 位置为结尾进行分析：

则dp[i][j]：到达[i, j]位置时的最低健康点数

状态转移方程：

dp[i][j]：到达[i, j]位置时的最低健康点数，由于一次只能向右或向下移动一步，因此[i, j]位置只能由[i-1, j] 或 [i, j-1]位置到达，

dp[i-1][j]：到达[i-1, j]位置的最低健康点数，因此，从[i-1, j]位置到达[i, j]位置的最低健康点数为 dp[i-1][j] - dungeon[i][j]

但是，dp[i-1][j] - dungeon[i][j]可能 <= 0，此时，骑士不能继续移动，要保证[i, j]位置的最低健康点数 >= 1，因此，需要修改dp[i-1][j]的值，而修改后，前面的值也需要进行修改，因此，以 [i, j]位置为结尾进行分析不可行

以[i, j]位置为结尾分析不行，我们以[i, j]位置为起点进行分析

dp[i][j]则表示：以[i, j]位置为起点，到达终点所学的最低健康点数

状态转移方程：

从[i, j]位置出发，则可到达[i+1, j] 和 [i, j+1]位置，

dp[i, j]：以[i, j]位置为起点，到达终点所学的最低健康点数，则dp[i+1][j]：到达[i+1, j]位置的最低健康点数

从 dp[i][j]位置走到dp[i+1][j]位置，则健康点数变为 dp[i][j] + dungeon[i][j]，即 dp[i+1][j] = dp[i][j] + dungeon[i][j]，因此 dp[i][j] = dp[i+1][j] - dungeon[i][j]

若 dungeon[i][j] < 0，当前位置需要消耗健康点数，则从[i, j]位置向下走时需要更多的健康点数

若 dungeon[i][j] > 0，当前位置会补充健康点数，则从[i, j]位置向下走时不需要很多健康点数，

但是，需要注意的是若 dungeon[i][j] > dp[i+1][j]时，dp[i+1][j] - dungeon[i][j] < 0，即当前位置能够补充很多健康点数（例如：dp[i+1][j] = 3，dungeon[i][j] = 4，dp[i+1][j] - dp[i][j] = -1，即到达当前位置的最低健康点数可为负数），但是题目中要求骑士的健康点数必须 >= 1，因此，当前的健康点数不能为0或负数，必须大于等于1，因此，[i, j]位置的最低健康点数为 max(1, dp[i+1][j] - dungeon[i][j])

同理，从 [i, j]位置走到[i, j+1]位置时的最低健康点数为 max(1, dp[i][j+1] - dungeon[i][j])

因此，[i, j]位置的最低健康点数dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])

初始化：

由于，dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]))，因此在填写最后一行和最后一列时可能会越界，因此，我们在最后一行的下面及最后一列的右面添加辅助节点来帮助我们进行初始化和赋值：

动态规划路径,Java刷题,动态规划,算法,java,leetcode

这样，在填写最后一行和最后一列时就不会发生越界

接下来，我们考虑：

1. 辅助节点里的值要保证后续填表过程中不出错

辅助节点能够帮助我们处理边界情况，但辅助节点里的值不能影响最终结果，当前位置不能到达辅助节点位置，即不能选择辅助节点里的值，dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]))，要选择两个元素中的最小值，我们可以将辅助节点中的值设为最大值，这样，就不会选择辅助节点中的值

但是，需要注意的是，当我们在填写终点的值时：

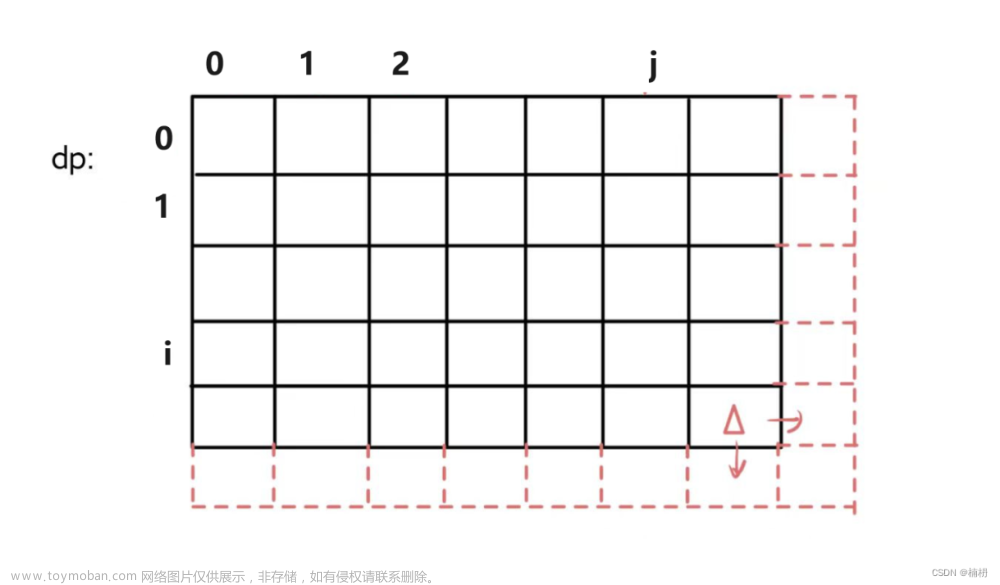
动态规划路径,Java刷题,动态规划,算法,java,leetcode

到达终点后，骑士的健康点数应该大于0，此时的最低健康点数应该为1，因此，应该将 dp[m][n-1] 或 dp[m-1][n]的值初始化为 1

2. 下标的映射关系

由于是在右侧和下侧添加的辅助节点，因此，dp[i][j]对应dungeon[i][j]

填表顺序：dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])，因此在填写[i, j]位置时要先知道[i+1][j] 和 [i][j+1]的值，因此，从下往上，每一行从右向左填写

返回值：要求从起点到重点的最低健康点数，因此，返回dp[0][0]

代码实现： 文章来源地址https://www.toymoban.com/news/detail-859929.html

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        //创建dp表
        int m = dungeon.length;
        int n = dungeon[0].length;
        int[][] dp = new int[m+1][n+1];
        //初始化
        for(int i = 0; i <= m; i++){
            dp[i][n] = Integer.MAX_VALUE;
        }
        for(int i = 0; i <= n; i++){
            dp[m][i] = Integer.MAX_VALUE;
        }
        dp[m][n-1] = 1;
        //填表
        for(int i = m-1; i >= 0; i--){
            for(int j = n-1; j >= 0; j--){
                dp[i][j] = Math.min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j];
                dp[i][j] = Math.max(1, dp[i][j]);
            }
        }
        //返回
        return dp[0][0];
    }
}

到了这里，关于动态规划——路径问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！