acwing算法提高之图论--最小生成树的典型应用-Toy模板网

这篇具有很好参考价值的文章主要介绍了acwing算法提高之图论--最小生成树的典型应用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

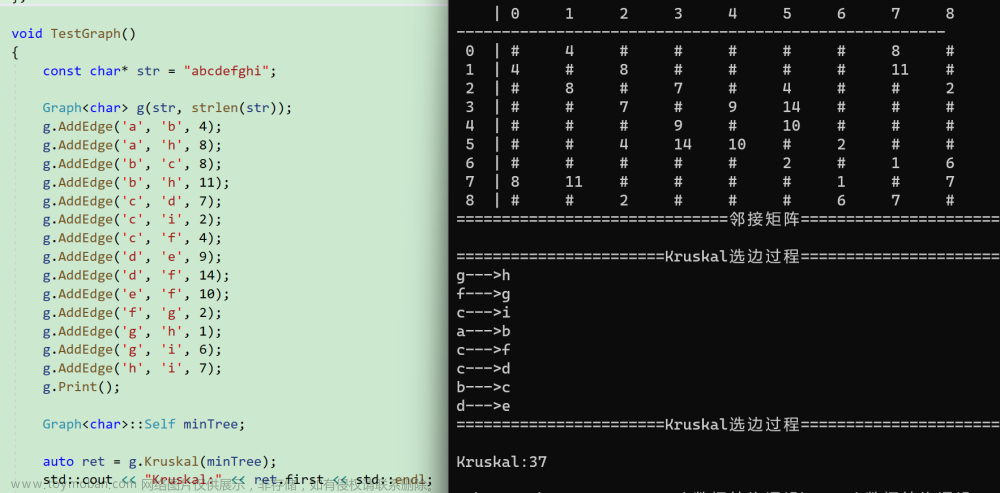
1 介绍

本专题用来记录使用prim算法或kruskal算法求解的题目。

2 训练

题目1：1140最短网络

C++代码如下，文章来源地址https://www.toymoban.com/news/detail-859986.html

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110, INF = 0x3f3f3f3f;
int g[N][N];
int d[N];
bool st[N];
int n, m;

void prim() {
    memset(d, 0x3f, sizeof d);
    
    int res = 0;
    for (int i = 0; i < n; ++i) {
        int t = -1;
        for (int j = 1; j <= n; ++j) {
            if (!st[j] && (t == -1 || d[t] > d[j])) {
                t = j;
            }
        }
        
        st[t] = true;
        if (i) res += d[t];
        
        for (int j = 1; j <= n; ++j) {
            if (d[j] > g[t][j]) {
                d[j] = g[t][j];
            }
        }
    }
    
    cout << res << endl;
    return;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            cin >> g[i][j];
        }
    }
    
    prim();
    
    return 0;
}

题目2：1141局域网

C++代码如下，

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110, M = 210;
int p[N];
int n, m;

struct Edge {
    int a, b, w;
    bool operator< (const Edge &W) const {
        return w < W.w;
    }
}edges[M];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin >> n >> m;
    int s = 0;
    for (int i = 0; i < m; ++i) {
        cin >> edges[i].a >> edges[i].b >> edges[i].w;
        s += edges[i].w;
    }
    
    for (int i = 1; i <= n; ++i) p[i] = i;
    
    sort(edges, edges + m);
    
    int res = 0, cnt = 0;
    for (int i = 0; i < m; ++i) {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a);
        b = find(b);
        if (a != b) {
            p[a] = b;
            res += w;
            cnt++;
        }
    }
    
    cout << s - res << endl;
    return 0;
}

题目3：1142繁忙的都市

C++代码如下，

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 310, M = 8010;
int n, m;
int p[N];

struct Edge {
    int a, b, w;
    bool operator< (const Edge &W) const {
        return w < W.w;
    }
}edges[M];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) p[i] = i;
    
    for (int i = 0; i < m; ++i) {
        cin >> edges[i].a >> edges[i].b >> edges[i].w;
    }
    
    sort(edges, edges + m);
    
    int res = 0;
    int cnt = 0;
    for (int i = 0; i < m; ++i) {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a);
        b = find(b);
        if (a != b) {
            p[a] = b;
            cnt += 1;
            res = w;
        }
    }
    
    cout << cnt << " " << res << endl;
    
    return 0;
}

题目4：1143联络员

C++代码如下，

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2010, M = 10010;
int n, m;
int p[N];
struct Edge {
    int a, b, w;
    bool operator< (const Edge &W) const {
        return w < W.w;
    }
}edges[M];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) p[i] = i;
    
    int res = 0;
    int j = 0;
    for (int i = 0; i < m; ++i) {
        int op, a, b, w;
        cin >> op >> a >> b >> w;
        if (op == 1) {
            res += w;
            a = find(a);
            b = find(b);
            if (a != b) {
                p[a] = b;
            }
        } else if (op == 2) {
            edges[j] = {a, b, w};
            j += 1;
        }
    }
    
    sort(edges, edges + j);
    for (int i = 0; i < j; ++i) {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a);
        b = find(b);
        if (a != b) {
            p[a] = b;
            res += w;
        }
    }
    
    cout << res << endl;
    
    return 0;
}

题目5：1144连接格点

C++代码如下，

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10, M = 2 * N;
int n, m;
int p[N];

struct Edge {
    int a, b, w;
    bool operator< (const Edge &W) const {
        return w < W.w;
    }
}edges[M];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n * m; ++i) p[i] = i;
    
    int x1, y1, x2, y2;
    while (cin >> x1 >> y1 >> x2 >> y2) {
        int w = 0;
        if (x1 == x2) w = 2;
        else w = 1;
        
        int a = (x1 - 1) * m + y1;
        int b = (x2 - 1) * m + y2;
        a = find(p[a]);
        b = find(p[b]);
        if (a != b) {
            p[a] = b;
        }
    }
    
    int k = 0;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j < m; ++j) {
            //(i,j) -> (i,j+1)
            int a = (i - 1) * m + j;
            int b = (i - 1) * m + j + 1;
            edges[k] = {a, b, 2};
            k += 1;
            
            //cout << "a = " << a << ", b = " << b << endl;
        }
    }
    
    //cout << "===" << endl;
    
    for (int j = 1; j <= m; ++j) {
        for (int i = 1; i < n; ++i) {
            
            //(i,j) -> (i+1,j)
            int a = (i - 1) * m + j;
            int b = i * m + j;
            edges[k] = {a, b, 1};
            k += 1;            
            
            //cout << "a = " << a << ", b = " << b << endl;
        }
    }
    
    sort(edges, edges + k);
    
    int res = 0;
    for (int i = 0; i < k; ++i) {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a);
        b = find(b);
        if (a != b) {
            p[a] = b;
            res += w;
        }
    }
    
    cout << res << endl;
       
    return 0;
}