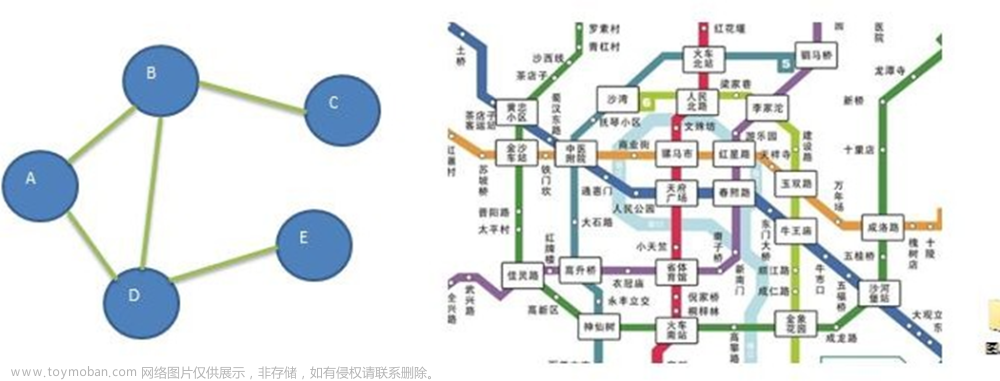
一、搜索与图论
1. DFS(深度优先遍历)
😋 时间复杂度:
邻接矩阵:O(v^2) (v是点数)
邻接表: O(v+m) (v是点数,m是边数)
😋 数字排列
static int n = 10;
static int[] path = new int[15]; // 存储数字的顺序
static boolean[] st = new boolean[15];// 数字使用状态,下标数字 一一对应
static void dfs(int u) { //参数是 树的层数,也就是排列数字的第 u 位
if (u == n) { //到最后一层,递归结束
for (int i = 0; i < n; i++)
System.out.print(path[i]);
System.out.println();
return;
}
for (int i = 1; i <= n; i++) {
if(!st[i]) {
path[u] = i;
st[i] = true;
dfs(u+1);
st[i] = false; // 数据保持一致,用了还 (回溯)
}
}
}
😋 n皇后问题(优化版)
//版本1 (每行只选一个格子)
static int N = 20; // 由于斜线的原因,至少开 2n-1 的空间
static int n; // n皇后问题
static char[][] g = new char[N][N]; // 存储皇后的信息
// 布尔类型默认值为 flase
static boolean[] col = new boolean[N]; // 列
// 正对角线 u = -i + b --> b = u + i
static boolean[] dg = new boolean[N];
// 反对角线 u = i + b --> b = u - i 但是 b 不能小于0,所以b = n - (u - i) = n - u + i
static boolean[] udg = new boolean[N];
static void dfs(int u) { // 这里的 u 是行号
// 递归出口
if (u == n) {
for (int i = 0; i < n; i++) { // 走到叶子结点,当前的g数组就是一个方案
for (int j = 0; j < n; j++) {
System.out.print(g[i][j] + " ");
}
System.out.println();
}
System.out.println();
}
for (int i = 0; i < n; i++) {
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false;
g[u][i] = '.';
}
}
}
public static void main(String[] args) {
n = 4; // 假装输入 4
// 初始化棋盘
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
g[i][j] = '.';
dfs(0);
}
😋 n皇后问题(初阶版)
// 版本2(从左上到右下,按格子放皇后)
static int N = 20; // 由于斜线的原因,至少开 2n-1 的空间
static int n; // n皇后问题
static char[][] g = new char[N][N]; // 存储皇后的信息
// 布尔类型默认值为 flase
static boolean[] col = new boolean[N]; // 列
static boolean[] row = new boolean[N]; // 列
// 正对角线 u = -i + b --> b = u + i
static boolean[] dg = new boolean[N];
// 反对角线 u = i + b --> b = u - i 但是 b 不能小于0,所以b = n - (u - i) = n - u + i
static boolean[] udg = new boolean[N];
/**
* @param x 行
* @param y 列
* @param s 皇后个数
*/
static void dfs(int x, int y, int s) {
if (y == n) {// 列标 溢出
y = 0;
x++;// 转到下一行
}
if (x == n) {
if (s == n) { // 放满8个皇后
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(g[i][j]);
}
System.out.println();
}
System.out.println();
}
return;
}
// 不放皇后
dfs(x, y + 1, s);
// 放皇后
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
g[x][y] = '.';
}
}
public static void main(String[] args) {
n = 4; // 假装输入 4
// 初始化棋盘
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
g[i][j] = '.';
dfs(0, 0, 0);
}
2. BFS
😋 时间复杂度
邻接矩阵:O(v^2) (v是点数)
邻接表: O(v+m) (v是点数,m是边数)
😋 迷宫最短路问题
static int N = 10;
static int[][] g = new int[N][N];// 图的数组
static int[][] d = new int[N][N];// 距离
static int[][] q = new int[N * N][2]; // 队列,存下标
static int n, m;// 行数 列数
static int bfs() {
int hh = 0, tt = 0; // 队列的头尾指针
// 初始化距离数组(注意 fill 只能对一维数组进行填充)
for (int i = 0; i < N; i++) {
Arrays.fill(d[i], -1);
}
q[0][0] = 0;
q[0][1] = 0;
d[0][0] = 0;
int[] dx = { -1, 0, 1, 0 }; // x向量
int[] dy = { 0, -1, 0, 1 }; // y向量
while (hh <= tt) {
// 队头出队
int xx = q[hh][0];
int yy = q[hh++][1];
for (int i = 0; i < 4; i++) {
int x = dx[i] + xx;
int y = dy[i] + yy;
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
d[x][y] = d[xx][yy] + 1;
q[++tt][0] = x;
q[tt][1] = y;
}
}
}
return d[n - 1][m - 1];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
g[i][j] = sc.nextInt();
}
}
System.out.println(bfs());
System.out.println();
}
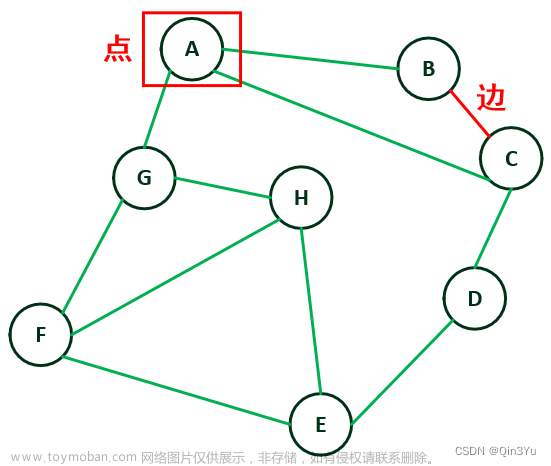
3. 图的DFS
😎 树的重心问题 参考地址
static int N = 100010;
static int M = 2 * N;
static int ans = N;
static int n, idx;
static int[] h = new int[N];// 头指针数组
static int[] e = new int[N];// 结点
static int[] ne = new int[N];// next指针数组
static boolean[] st = new boolean[N];// 记录点有没有被遍历
// 添加结点 a 指向 结点 b 的边
static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
// 深度优先遍历
/**
* @param u 要搜索的结点下标
* @return 返回 u 结点所在图的结点树
*/
static int dfs(int u) {
st[u] = true; // 记录下已经遍历的结点,防止重复遍历
int size = 0; // 连通块的最值
int sum = 0;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
// 重复结点,跳过
if (st[j])
continue;
int s = dfs(j);// 深搜子结点
size = Math.max(size, s); // 更新连通块的最值
sum += s; // u结点的所有子结点拥有的结点数加起来 sum
}
size = Math.max(size, n - sum - 1); // u的子连通块的最小连通数 ; u 的父连通块的结点数
ans = Math.min(size, ans); // 找最小连通块的结点个数
return sum + 1; // 子结点的连通块个数 加上 本身 1个
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
// 初始化邻接表(链表)
Arrays.fill(h, -1);
for (int i = 0; i < n - 1; i++) { // 读取边数据,初始化图,边数比结点数少 1
int a = sc.nextInt();
int b = sc.nextInt();
add(a, b);
add(b, a);
}
dfs(1);// 随便传一个点
System.out.println(ans);
}
4. 图的BFS
😎 图中点的层次 参考地址
static int n, m, idx;
static int N = 10010;
static int[] e = new int[N];
static int[] ne = new int[N];
static int[] h = new int[N];
static int[] d = new int[N];
static int[] q = new int[N];
static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
static void bfs() {
Arrays.fill(d, -1);
q[0] = 1;
d[1] = 0;
int hh = 0, tt = 0;
while (hh <= tt) {
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] == -1) // 条件成立,当前结点没有被搜索到过
{
d[j] = d[t] + 1;
q[++tt] = j; // 插入到队列中
}
}
}
System.out.println(d[n]);
}
public static void main(String[] args) {
Arrays.fill(h, -1);
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 1; i <= m; i++) {
int a, b;
a = sc.nextInt();
b = sc.nextInt();
add(a, b);
}
bfs();
}
5. 图的拓扑序列
😎 有向,无环的图才有拓扑序列 参考地址
static int N = 100010;
static int idx, n, m;
static int[] e = new int[N];// 结点值数组
static int[] ne = new int[N];// next指针数组
static int[] h = new int[N];// 头指针数组
static int[] q = new int[N];// 队列
static int[] d = new int[N];// 入度数
// a ---> b
static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
static boolean topSort() {
int hh = 0, tt = -1;
for (int i = 1; i <= n; i++) { // 这里必须是从 1 到 n,因为点的编号从 1 开始,没有 0
if (d[i] == 0) {
q[++tt] = i; // 将所有入度为 0 的点入队
}
}
while (hh <= tt) {
int t = q[hh++];// 当前结点
for (int i = h[t]; i != -1; i = ne[i]) {// 遍历当前结点的所有后继结点
int j = e[i]; // 获取当前结点的后继结点的值
d[j]--; // 删除点 t 指向 点 j 的边
if (d[j] == 0) // 如果点 j 的入度为零了,入队
q[++tt] = j;
}
}
// 表示如果n个点都入队了的话,那么该图为拓扑图,返回true
return tt == n - 1;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
// 初始化头指针数组
Arrays.fill(h, -1);
for (int i = 0; i < m; i++) {
int a, b;
a = sc.nextInt();
b = sc.nextInt();
add(a, b);// a指向b ,b的入度 +1
d[b]++;
}
if (topSort()) {
for (int i = 0; i < n; i++) {
System.out.print(q[i]);
}
System.out.println();
} else {
System.out.println(-1);
}
}
6. Dijkstra(迪杰斯特拉)
适用范围:单源无负权边
😉 朴素版 O(n^2)
😉 适用于稠密图 即 n个点 n^2条边
😉 参考链接
import java.util.*;
class Main{
static int N = 550,n,m,INF = 0x3f3f3f3f;
static int[][] g = new int[N][N];//邻接矩阵存图
static boolean[] st = new boolean[N];
static int[] dist = new int[N];
static int dijkstra()
{
Arrays.fill(dist,INF);
dist[1] = 0;
for(int i = 0; i < n; i++)//找n次最小距离的点
{
int t = -1;
for(int j = 1; j <= n; j++)//循环找当前最小距离的点
{
if(!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
}
st[t] = true;
for(int j = 1; j <= n; j++)//用当前最小距离的点试图去更新其他的距离
{
dist[j] = Math.min(dist[j],dist[t] + g[t][j]);
}
}
if(dist[n] == INF)
return -1;
else
return dist[n];
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for(int i = 0; i <= n; i++)
{
Arrays.fill(g[i],INF);//初始化边权(全部默认为无边【无穷大】)
}
for(int i = 0; i < m; i++)
{
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
g[a][b] = Math.min(g[a][b],c);//处理重边。直接保留最短的边即可
}
System.out.println(dijkstra());
}
}
😍 堆优化版 O(m Log n)
😍 适用稀疏图
static int N = 1000010;
static int[] e = new int[N], ne = new int[N], h = new int[N], w = new int[N];// 邻接表
static int idx;
static int[] dist = new int[N];// 距离数组
static boolean[] st = new boolean[N];// 是否已经求得最短路径
static int n, m;
static void add(int x, int y, int z) {
e[idx] = y;
w[idx] = z;
ne[idx] = h[x];
h[x] = idx++;
}
static int dijkstra() {
// 初始化距离
Arrays.fill(dist, 0x3f3f3f3f);
dist[1] = 0;
PriorityQueue<pair> heap = new PriorityQueue<>((o1, o2) -> (o1.d - o2.d));// 按距离升序排小根堆
pair pair = new pair(0, 1);
heap.add(pair);
while (heap.size() != 0) {
pair t = heap.peek();// 小顶堆,堆顶即是最小路径的点
heap.poll();
int ver = t.x; // vertex :顶点
int distance = t.d;
if (st[ver]) {
continue;// 如果该点已经确定了最短距离那就跳过
}
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > distance + w[i]) {
dist[j] = distance + w[i]; // 更新距离
heap.add(new pair(dist[j], j));
}
}
}
if (dist[n] == 0x3f3f3f3f)
return -1;
else
return dist[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
// 初始化邻接表
Arrays.fill(h, -1);
for (int i = 0; i < m; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
add(x, y, z);
}
System.out.println(dijkstra());
}
static class pair {
int d;// 存 到该点距离
int x;// 存 点
public pair(int d, int x) {
super();
this.d = d;
this.x = x;
}
}
7. Bellman-Ford(贝尔曼福特)
😚 适用范围:单源有负权边
😋 有边数限制的最短路:原题地址
😋 算法复杂度: O(nm)
static int N = 510;
static int M = 10010;
static Edge[] edges = new Edge[M];// 存储所有的边
static int[] dist = new int[N];// 距离数组
static int[] backup = new int[N];// 备份数组,用于防止连环更新
static int n, m, k;// k是题目限制的边数
static class Edge { // 自定义一个边类
int a, b, w;
public Edge(int a, int b, int w) {
this.a = a;
this.b = b;
this.w = w;
}
}
static int bellmanFord() {
// 初始化
Arrays.fill(dist, 0x3f3f3f3f);
dist[1] = 0;
for (int i = 0; i < k; i++) {// 题目限制多少条边,那就循环多少次
backup = Arrays.copyOf(dist, dist.length);// 数组的备份
for (int j = 0; j < m; j++) {
int a = edges[j].a;
int b = edges[j].b;
int w = edges[j].w;
//用备份的数据更新其他结点的距离。【 就是避免了 b 被更新后,下一循环再作为 a更新其他的边】
dist[b] = Math.min(dist[b], backup[a] + w);
}
}
// 0x3f3f3f3f/2 是避免到不了的非联通图的情况,无穷 + 负边 < 无穷 。所以不能用无穷判断
// 为什么是 无穷 / 2 呢? 因为边的权重范围 <10000 点的数量 <500 。 所以: 无穷 - 五百万 > 无穷 / 2
if (dist[n] > 0x3f3f3f3f / 2)
return 0x3f3f3f3f;
else
return dist[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
k = sc.nextInt();
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int w = sc.nextInt();
edges[i] = new Edge(a, b, w);
}
int t = bellmanFord();
if (t == 0x3f3f3f3f)
System.out.println("impossible");
else {
System.out.println(t);
}
}
8. spfa算法
😘 适用条件:不能有负环
😘 时间复杂度:[最坏] O(n m)
😘spfa求最短路 参考地址
static int N = 100010;
static int n, m, idx;
static int[] e = new int[N];// 结点数组
static int[] w = new int[N];// 权重
static int[] ne = new int[N];// next数组
static int[] h = new int[N];// 头指针
static int[] dist = new int[N];// 距离
static boolean st[] = new boolean[N];// 结点是否已经入队
static void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
static int spfa() {
Arrays.fill(dist, 0x3f3f3f3f);
LinkedList<Integer> q = new LinkedList<>();// LinkedList 实现了 Queue 接口,可以当成队列用
// 初始化距离
dist[1] = 0;
q.add(1); // 入队用add,而不是用 push
st[1] = true;
while (!q.isEmpty()) {
int t = q.poll();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
// 获取i点的编号,判断是否有变小,若变小,入队
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
if (!st[j]) {
q.add(j);
st[j] = true;
}
}
}
}
return dist[n];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
Arrays.fill(h, -1);
while (m-- > 0) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
add(a, b, c);
}
if (spfa() == 0x3f3f3f3f)
System.out.println("impossible");
else {
System.out.println(dist[n]);
}
}
9. Floyd(弗洛伊德)
👵 时间复杂度:O(n^3)
🥰 多元汇求最短路:参考地址
static int N = 210;
static int INF = 0x3f3f3f3f;// 无穷大
static int n, m, k, x, y, z;
static int[][] d = new int[N][N];// 邻接矩阵
static void floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);
}
}
// 弗洛伊德
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
k = sc.nextInt();
// 初始化邻接矩阵
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j)
d[i][j] = 0;// 自身与自身的距离直接是0,消去自环
else
d[i][j] = INF;
}
}
// 读入边
while (m-- > 0) {
x = sc.nextInt();
y = sc.nextInt();
z = sc.nextInt();// 权值
d[x][y] = Math.min(d[x][y], z);// 重边取最小值
}
floyd();
// 读入询问
while (k-- > 0) {
x = sc.nextInt();
y = sc.nextInt();
if (d[x][y] > INF / 2)
System.out.println("impossible");
else
System.out.println(d[x][y]);
}
}
10. Prim (普利姆)
🥰 prim 算法求最小生成树: 参考地址
🥰 时间复杂度:O(n^2)
static int N = 510;
static int INF = 0x3f3f3f3f;
static int n, m, u, v, w;
static int[][] g = new int[N][N];// 邻接矩阵存图
static int[] dist = new int[N];// 存每一个点到 【生成树】 的距离
static boolean[] st = new boolean[N];
static int prim() {
// 初始化距离数组
Arrays.fill(dist, INF);
int res = 0;// 记录最小生成树所有边的权值和
// n个点n次迭代
for (int i = 0; i < n; i++) {
int t = -1;// 定义 -1 为了第一点所有距离都是无穷的时候能加入到树中
for (int j = 1; j <= n; j++) {
// 找到没加入生成树中的点与集合边 中的最小边
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
if (i != 0 && dist[t] == INF)
return dist[t];
if (i != 0)
res += dist[t];
st[t] = true;
// 更新其他点到新集合的距离
for (int j = 1; j <= n; j++) {
dist[j] = Math.min(dist[j], g[t][j]);
}
}
return res;
}
public static void main(String[] args) {
// 一定要初始化 图
for (int i = 0; i < g.length; i++) {
Arrays.fill(g[i], INF);
}
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
while (m-- > 0) {
u = sc.nextInt();
v = sc.nextInt();
w = sc.nextInt();
g[u][v] = g[v][u] = Math.min(g[u][v], w);
}
int t = prim();
if (t == INF)
System.out.println("impossible");
else {
System.out.println(t);
}
}
11. Kruskal (克鲁斯卡尔)
🥰 克鲁斯卡尔算法求最小生成树(结合并查集)
🥰 时间复杂度:O(mlogm)
🥰 参考地址
static int N = 100010;
static int M = 200010;
static int INF = 0x3f3f3f3f;
static int n, m, a, b, w;
static int[] p = new int[N];// 并查集
static Edge[] e = new Edge[N];
// 并查集本并,返回值就是所在的 集合
static int find(int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
static int kruskal() {
int res = 0;// 记录当前生成树的权值和
int cnt = 0;// 记录当前生成树边的数量
// 将边按权值排序 sort(char[] a, int fromIndex(包含), int toIndex(不包含))
// 按升序排列数组的指定范围。
Arrays.sort(e, 0, m);// 一定要控制范围,因为数组开大了,有未初始化的值
// 从小到大枚举所有边
for (int i = 0; i < m; i++) {
// 获取当前边的起点和终点
int s = e[i].s;
int t = e[i].t;
int w = e[i].w;
// 并查集判断两点是否在同一个 最小生成树中
s = find(s);
t = find(t);
if (s != t) {// 如果不在同一个集合
p[s] = t; // 并查集的合并
res += w; // 更新总权重
cnt++;
}
}
if (cnt < n - 1) {// n个结点,至少要 n-1 条边才能是连通的
return INF;
}
return res;
}
public static void main(String[] args) throws IOException {
// 大数据量输入
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] s1 = br.readLine().split(" ");
n = Integer.parseInt(s1[0]);
m = Integer.parseInt(s1[1]);
// 初始化并查集,读入边
for (int i = 1; i <= n; i++) {
p[i] = i;
}
for (int i = 0; i < m; i++) {
String[] s2 = br.readLine().split(" ");
a = Integer.parseInt(s2[0]);
b = Integer.parseInt(s2[1]);
w = Integer.parseInt(s2[2]);
e[i] = new Edge(a, b, w);
}
int t = kruskal();
if (t == INF)
System.out.println("impossible");
else {
System.out.println(t);
}
}
}
//自定义一个 Edge 类,实现 comparable 接口便于排序
class Edge implements Comparable<Edge> {
int s;// 起点
int t;// 终点
int w;// 权值
@Override
public int compareTo(Edge e) { // 重写compareTo方法,小减大,升序
return this.w - e.w;
}
public Edge(int s, int t, int w) {
super();
this.s = s;
this.t = t;
this.w = w;
}
12. 染色法
😋 二分图:
😋 将所有点分成两个集合,所有边都在集合之间,那就是二分图
😋 一定不含有奇数环
😎 染色法判断二分图:参考地址
🥰 时间复杂度: O(n+m)
static int N = 100010;
static int n, m, u, v, idx;
// 邻接表存边
static int[] e = new int[N];
static int[] ne = new int[N];
static int[] h = new int[N];
static int[] st = new int[N];// 0 表示没染色 1,2 表示两种不同颜色
static void add(int u, int v)
{
// u 指向 v 的边,无向图就就加来回两条
e[idx] = v;
ne[idx] = h[u];
h[u] = idx++;
}
static boolean dfs(int u, int c)
{
st[u] = c;// 染色
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (st[j] == 0)
{
// 神之 3 - c ,这样 c 就能间隔地取到 1 和 2 的值了
if (!dfs(j, 3 - c))// 染色失败,说明矛盾了
return false;
} else if (st[j] == c)
return false;// 当前点和邻接点颜色相同了,矛盾返回 false
}
return true;// 所有染色过程都成功了,返回true
}
public static void main(String[] args)
{
// 初始化边头指针数组
Arrays.fill(h, -1);
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 0; i < m; i++)
{
u = sc.nextInt();
v = sc.nextInt();
// 无向图,加两条
add(u, v);
add(v, u);
}
boolean flag = true;// 记录是否染色成功
for (int i = 0; i <= n; i++)
{
if (st[i] == 0)
{// 点 i 没染色
if (!dfs(i, 1))// 染色失败
{
flag = false;
break;
}
}
}
if (flag)
System.out.println("Yes");
else
System.out.println("No");
}
13. 匈牙利算法
👵 时间复杂度:O(vm) (v是一边集合的点数,m是边数)
👵 匈牙利算法求二分图的最大匹配:参考地址
static int N = 510;
static int M = 100010;
static int n1, n2, m, idx, a, b;
// 边数组一定要开 大于 M 边数 的大小
static int[] e = new int[M];
static int[] ne = new int[M];
static int[] h = new int[N];
static boolean[] st = new boolean[N];// 判断是否重复
static int[] match = new int[N];
static void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
static boolean find(int x)
{
for (int i = h[x]; i != -1; i = ne[i]) // 列举 x 结点邻接的所有边对应的点
{
int j = e[i];// j 是待匹配的点
//只有当 j 没被匹配才会进来,所以当第二次find(match[j])的时候,就会给x结点分配下一个待匹配的j结点
// 如果实在没有可以匹配的了,返回 false
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
n1 = sc.nextInt();
n2 = sc.nextInt();
m = sc.nextInt();
// 初始化边
Arrays.fill(h, -1);
while (m-- > 0)
{
a = sc.nextInt();
b = sc.nextInt();
add(a, b);
}
int res = 0;
for (int i = 1; i <= n1; i++)// 给左子集的所有点找匹配
{
Arrays.fill(st, false);// 初始化判重数组
if (find(i))
res++;// 给i点找匹配,成功则 res++
}
System.out.println(res);
}
二、数学知识
1. 质数(素数)
🤠 试除法
🤠 O( sqrt(n) )
// 判断质数(素数)的方法
boolean ifPrime(int x) {
if(x < 2) return false;
// 试除法(试除到 根号x即可,因为因数是成对存在的)
/*
例 : 6
1*6 2*3 3*2 6*1
左右对称,只需枚举一半即可(根号x)
*/
for(int i = 2; i <= x/i; i++) {
if(x%i == 0) return false;
}
return true;
}
2. 分解质因数
😏 参考地址:acwing案列
😏 最坏:O( sqrt(n) )
static void divide(int x)
{
// 大于 根号x 的质数中 只有本身能整除本身
for (int i = 2; i <= x / i; i++)
{
if (x % i == 0)
{
int s = 0;// 指数
while (x % i == 0)
{
x /= i;
s++;
}
System.out.print(i + " " + s);
}
System.out.println();
}
// 当x没能被 2 到 根号x 任何一个数整除时,说明它本身就是一个质数
if (x > 1)
System.out.println(x + " " + 1);
System.out.println();
}
3. 筛素数
👼 参考地址:埃氏筛选法
👼 原理:用找到的素数把后边的合数去掉
👼 O( nlog(logn) )
static int cnt;
static int N = 100000010;
static int[] primes = new int[N];
static boolean st[] = new boolean[N];// true 表示合数
static int getPrime(int n)
{
for (int i = 2; i <= n; i++)
{
// st[i] = false 素数
if (!st[i])
{
primes[cnt++] = i;
// 把以素数为因数的数都去掉 2i,3i,4i ...
for (int j = 2; j * i <= n; j++)//条件要控制筛选到 n
{
st[i * j] = true;
}
}
}
return cnt;
}
😏 线性筛法
😏 O(n)
static int N = 100010;
static int cnt;// 存储素数的个数
static int[] primes = new int[N];// 存储素数的数组
static boolean[] st = new boolean[N];
static void getPrimes(int n)
{
for (int i = 2; i <= n; i++)
{
if (!st[i])
primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j++)
{
// 小于最小质因子的所有 【质数 * i】 =【结果】的最小质因子 都是 当前质数 ,而且是合数所以可以去掉
st[primes[j] * i] = true; //质数 乘以 某数 肯定时 合数
// 控制只以比最小质数小的质数 筛选,比如 20 用 2筛掉了就不会用 5再筛一次
// 因为筛到最小质数时,已经把后边要筛的都筛完了
// 例 12 = 4*3 = 2*2*3 = 2*6 而 4 筛选的都会被它的最小质因子 2 筛掉,so只要筛到 2 就够了
if (i % primes[j] == 0)
break; // j 从小到大开始遍历,所以 primes[j]一定是 i 的最小质因子
}
}
}
4. 试除法求约数
🤔 参考地址:acwing
🤔 O ( sqrt(n) )
/**
* @param x 待求约数的数
* @return 所有约数组成的数组
*/
static ArrayList<Integer> getDivitors(int x)
{
ArrayList<Integer> list = new ArrayList<>();
for (int i = 1; i <= x / i; i++)
{
if (x % i == 0)
{
list.add(i);
if (i != x / i)// 排除 x = i*i 时 i重复加入的情况
list.add(x / i);
}
}
list.sort(null);//传一个 null 参数就是自然升序
return list;
}
5. 约数个数
👨🦰 参考地址:acwing
static int mod = 1000000007;
public static void main(String[] args)
{
HashMap<Integer, Integer> map = new HashMap<>();// 存的是指数
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n-- > 0)
{
int x = sc.nextInt();
for (int i = 2; i <= x / i; i++)// i 从2开始
{
while (x % i == 0) //while 循环,直到开不出因数 i 为止
{
map.put(i, map.getOrDefault(i, 0) + 1);
x /= i;
}
}
// 特判:当 x 本身就是一个质数的情况
if (x != 1)
map.put(x, map.getOrDefault(x, 0) + 1);
}
long res = 1;
for (int i : map.values())
{
res = res * ((i + 1)) % mod; // 加 1 是因为有指数为 0 的情况
}
System.out.println(res);
}
6. 约数求和
🐷 约数和定理:百度百科
🐷 把每一项乘出来就是 n 的所有约数相加了
🐷 参考地址
static long mod = 1000000007;
public static void main(String[] args)
{
HashMap<Integer, Integer> map = new HashMap<>();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n-- > 0)
{
int x = sc.nextInt();
for (int i = 2; i <= x / i; i++)
{
while (x % i == 0)
{
map.put(i, map.getOrDefault(i, 0) + 1);
x /= i;
}
}
if (x != 1)
map.put(x, map.getOrDefault(x, 0) + 1);
}
long res = 1;
// 根据约数和定理
for (int p : map.keySet())
{
//① 先求每一个小括号里的值
long sum = 0;
int a = map.get(p);
long t = 1;
// 这里 p 是底数 a 是指数
while (a-- > 0)
{
/* 加一 ? 例:2 的 4次 或者说 +1 就是 p 的 0 次幂
a t p t = t * p + 1
3 1 2 t = 1 * 2 + 1 = 3
2 3 2 t = 3 * 2 + 1 = (2 + 1) * 2 + 1 = 2^2 + 2^1 + 2^0 = 7
1 7 2 t = 7 * 2 + 1 = (2^2 + 2^1 + 2^0) * 2 + 1 = 2^3 + 2^2 + 2^1 + 1 = 15
总结 *p 就是之前的 t 所有的 p 指数 +1,但是 0 次方的就消掉了,然后每次都得补上 +1
*/
t = (t * p + 1) % mod;
}
// ② 把的每一个值乘起来就是所有约数的和了
res = res * t % mod;
}
System.out.println(res);
}
7. 最大公约数
✨ 辗转相除法(欧几里得算法)
✨ O( log n)
static long gcd(long a, long b)
{
/* 辗转相除法
求 a,b 的公约数 == 求 a,b+ka 的公约数
例:求公约数的数 公约数
12,18 6
12,18+12=30 6
30 18 6
12,18+24=42 6 总结可知:a,b 的公约数 == a,b%a 的公约数
*/
return b != 0 ? gcd(b, a % b) : a;
}
8. 欧拉函数
✨ 欧拉函数求互质的数的个数:参考地址

✨ 互质数:只有一个共同公因数 1 的两个数
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n-- > 0)
{
int a = sc.nextInt();
int res = a;
for (int i = 2; i <= a / i; i++)
{
if (a % i == 0)// 条件成立,i 就是 a 的一个质因子
{
// 欧拉方程
// res = res *(1-1/i);//整除运算不能有小数, 1/i 得换掉,把 1/i 提出去
res = res / i * (i - 1);
while (a % i == 0)//只要 a 还有 i 这个质因子就进去
a /= i;
}
}
if (a > 1)//质因子只有1和本身的情况
res = res / a * (a - 1);
System.out.println(res);
}
}
9. 筛法求欧拉函数
✨ 参考地址
✨ 思路分析
static int N = 1000010, cnt;
static int[] primes = new int[N];// 素数数组
static int[] phi = new int[N]; // 欧拉数组
static boolean[] st = new boolean[N];
static long getEulers(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; i++)
{
if (!st[i])
{
primes[cnt++] = i;
phi[i] = i - 1;// 素数的情况
}
for (int j = 0; primes[j] <= n / i; j++)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0)
{
phi[primes[j] * i] = phi[i] * primes[j];
break;
}
phi[primes[j] * i] = phi[i] * (primes[j] - 1);
}
}
long res = 0;
for (int i = 1; i <= n; i++)
res += phi[i];
return res;
}
public static void main(String[] args)
{
// 测试案例
// 输入 6 输出 12
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(getEulers(n));
}
10. 快速幂
✨ 参考传送门
✨ O( Log k)
✨ 注意:10的9次方已经达到 int 的临界值,要用 long 类型
/**快速幂
* @param a 底数
* @param k 幂数
* @param p 模
* @return a ^ k % p = ?
*/
static int qmi(int a, int k, int p)
{
int res = 1;
while (k != 0)
{
if ((k & 1) != 0)
{
res = res * a % p;
}
k >>= 1;// k/2
a = a * a % p;
}
return res;
}
✨ 快速幂求逆元
✨ 乘法逆元的作用
✨ 费马小定理
✨ 思路:先化简,然后观察方程,刚好符合费马小定理,然后套快速幂公式

/**
* 快速幂
*
* @param a 底数
* @param k 幂数
* @param p 模
* @return a ^ k % p = ?
*/
static int qmi(int a, int k, int p)
{
int res = 1;
while (k != 0)
{
if ((k & 1) != 0)
{
res = res * a % p;
}
k >>= 1;// k/2
a = a * a % p;
}
return res;
}
public static void main(String[] args)
{
// 快速幂求逆元
int a = 6;
int p = 3;
int res = qmi(a, p - 2, p);
if (a % p != 0) // a 不能是 p 的倍数,并且 p 不等于 2
{
System.out.println(res);
} else
{
System.out.println("impossible");
}
}
11. 扩展欧几里得算法
✨ 参考传送门
static int x, y, tem;
// 扩展欧几里得算法
static int x, y, tem;
// 扩展欧几里得算法
static int exGcd(int a, int b)
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
int gcd = exGcd(b, a % b);
tem = x;
x = y;
y = tem;
y -= a / b * x;
return gcd;
}
public static void main(String[] args)
{
// exGcd(4, 6);// -1 1
exGcd(8, 18);// -2 1
System.out.println(x + " " + y);
}
12. 高斯消元
✨ 死去的线性代数正在攻击我的脑子……
✨ 核心思路:初等行变换
✨ 参考传送门
static int N = 110;
static double eps = 0.000001;// 极小值,由于 double 精度问题,只要某数小于 eps 即是 0
static double[][] a = new double[N][N];// 注意从下标 1 开始存数据
static int n;// 记录有多少方程组
/**
* @return 0代表唯一解,1代表无穷多组解,2代表无解
*/
static int gauss()
{
int c = 1;// 当前列 colum
int r = 1;// 当前行 row
for (c = 1; c <= n; c++)// 遍历每一行
{
int t = r;// 临时变量记录当前列绝对值最大的行
// 1. 找出绝对值最大的行
for (int i = r; i <= n; i++)
{
if (Math.abs(a[i][c]) > Math.abs(a[t][c]))
t = i;// 更新最大值所在行
}
// 当 a[t][c] == 0 时,说明此行已经处理过了。注意:a[t][c]在这一列中绝对值最大
if (Math.abs(a[t][c]) < eps)
continue;
// 2. 将选中的这一行调到未处理行中 的最上面
if (t != r)
{
// 交换行
for (int j = c; j <= n + 1; j++)
{
double tem = a[t][j];
a[t][j] = a[r][j];
a[r][j] = tem;
}
}
// 3. 将首位非零的数化成 1
for (int j = n + 1; j >= c; j--)
{
a[r][j] /= a[r][c];
}
// 4. 将 该列 本行之下 的所有元素都置为 0
for (int i = r + 1; i <= n; i++) // 此时 i 表示要置 0 的行标
{
if (Math.abs(a[i][c]) > eps)// 不等于 0 进来
for (int j = n + 1; j >= c; j--)// 注意:从后边开始减去 ( 1* 不为0的元素值 )
a[i][j] = a[i][j] - a[i][c] * a[r][j];
}
// print();
r++;
}
// 走了continue,说明有一列全都是 0,即 0*x = ?,如果方程右边不是 0 ,w无解
if (r < n + 1)// 方程数小于 n
{
for (int i = r; i <= n; i++)// ?
if (Math.abs(a[i][n + 1]) > eps)
return 2;// 无解
return 1;// 无穷多解
}
// 然后就是唯一解的情况
// 最后一个解已知,借助最后一个解,求出其他的解
for (int i = n - 1; i >= 1; i--)
{
// 每次都是从对角线上的元素后一个元素开始解
// (通过下边已知的解把对应的列化0,使该行只剩下对角线上的系数不为 0 )
for (int j = i + 1; j <= n; j++)
{
a[i][n + 1] -= a[i][j] * a[j][n + 1];// 此时,a[j][n+1] == 1
}
}
return 0;
}
/*
输入:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出
1.00
-2.00
3.00
*/
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n + 1; j++)
{
a[i][j] = sc.nextDouble();
}
}
int t = gauss();
// 0 代表唯一解,1代表无穷解,2代表无解
if (t == 0)
for (int i = 1; i <= n; i++)
System.out.println(a[i][n + 1]);
else if (t == 1)
System.out.println("Infinite group solutions");
else
System.out.println("No solution");
}
// 输出调试
static void print()
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n + 1; j++)
System.out.printf("%4f ", a[i][j]);
System.out.println();
}
System.out.println();
}
13. 组合数
(1)组合数 1
✨ 案列传送门
✨ 核心思路:c[ i ][ j ] = c[ i-1 ][ j-1 ] + c[ i-1 ][ j ] 【预处理】
static int N = 2010, mod = 1000000007;
static int[][] c = new int[N][N];// 组合数 数组
// 预处理
static void init()
{
for (int i = 0; i < N; i++)
for (int j = 0; j <= i; j++)
if (j == 0)//处理边界
c[i][j] = 1;
else
{
// 从i个数选j个数 = 【(选定一个数)再从 i-1 个数 挑 j-1 个数】+ 【(不选某个数)从i-1 个数中挑 j 个数】
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
}
public static void main(String[] args)
{
/*
输入:
3
3 1
5 3
2 2
输出:
3
10
1
*/
init();
// 测试案例
System.out.println(c[3][1]);
System.out.println(c[5][3]);
System.out.println(c[2][2]);
}
(2)组合数 2
✨ 乘法逆元
✨ 参考传送门
✨ 注意转为 long 类型防止溢出
✨ 两层强转注意小括号表明嵌套关系
static int N = 100010, mod = (int) 1e9 + 7;
static int[] fact = new int[N];// 阶乘 数组
static int[] infact = new int[N];// 逆元数组
/**
* @param a 底数
* @param k 指数
* @param p 模
* @return
*/
static int qmi(int a, int k, int p)
{
long res = 1;
while (k > 0)
{
if ((k & 1) != 0)
res = res * a % p;
//
a = (int) ((long) a * a % p);
// a = (int) (long) a * a % p; 错误案例
// 两层强转的时候后边的待强转数要加 小括号
k >>= 1;
}
return (int) res;
}
public static void main(String[] args)
{
fact[0] = infact[0] = 1;// 初始化
for (int i = 1; i < N; i++)
{
// 求阶乘
fact[i] = (int) (long) fact[i - 1] * i % mod;
// 求逆元的阶乘
infact[i] = (int) ((long) infact[i - 1] * qmi(i, mod - 2, mod) % mod);
}
int a = 5;
int b = 3;
// 输出 10
// c[a][b] = a! / ( (a-b)! * b! )
System.out.println((int) ((long) fact[a] * infact[b] % mod * infact[a - b] % mod));
}
(3)组合数 3
✨ 鲁卡斯定理
✨ 参考传送门
✨ 注意运算过程中的溢出问题
static long p;
// 快速幂
static long qmi(long a, long k)
{
long res = 1;
while (k > 0)
{
if ((k & 1) == 1)
res = res * a % p;
a = a * a % p;
k >>= 1;
}
return res;
}
// 计算组合数的方法
/**
* @param a 上标
* @param b 下标
* @return 组合数的值
*/
static long C(long a, long b)
{
long res = 1;
// 从 a 向下乘 b 步,然后除以 b的阶乘(乘以其逆元)
for (int i = 1, j = (int) a; i <= b; i++, j--)
{
res = res * j % p;
res = res * qmi(i, p - 2) % p;
}
return res;
}
static long lucas(long a, long b)
{
if (a < p && b < p)
return C(a, b);
return C(a % p, b % p) * lucas(a / p, b / p) % p;
}
public static void main(String[] args)
{
// 测试数据
long a = 6;
long b = 4;
p = 13;
System.out.println(lucas(a, b));
}
(3)组合数 4
✨ 求质因子的个数
✨ 例:求 12! 中 有多少个2相乘

✨ 参考传送门
static int N = 5050;
static int cnt;//默认自动初始化为 0
static int[] primes = new int[N];//质数数组
static int[] sum = new int[N];//记录质数的指数(即有多少个 特定质数 相乘)
static boolean[] st = new boolean[N];//已筛标志 数组
static ArrayList<Integer> res = new ArrayList<>();
// 线性筛(质数)
/**
* @param n 筛选 0~n 的质数
*/
static void getPrimes(int n)
{
for(int i =2; i <= n; i++)
{
if(!st[i])
primes[cnt++] = i;
for(int j =0; primes[j] <= n/i; j++)
{
st[primes[j]*i] = true;
if(i % primes[j] == 0) break;
}
}
}
// 高精度乘法(从低位开始算)
static void multi(int b)
{
int t = 0;
for(int i = 0; i < res.size(); i++)
{
t += res.get(i) * b;
res.set(i, t%10);
t /=10;//存进位
}
while(t>0)
{
res.add(t%10);
t /= 10;
}
// 消去高位的 0
while(res.size()>1 && res.get(res.size()-1) ==0)
res.remove(res.size()-1);
}
static int get(int n,int p)
{
int res = 0;
while(n>0)
{
res += n/p;
n /= p;
}
return res;
}
public static void main(String[] args)
{
int a = 5,b = 3;//求 C[b][a] , 输出 10
getPrimes(a);
for(int i =0; i<cnt;i++)
{
int p = primes[i];
// a! 中 p的指数 - b! 中p的指数 - (a-b)! 中p的指数
// == [a]/([b]*[a-b]) (简版)
sum[i] = get(a,p) - get(b,p) - get(a-b,p);
}
res.add(1);//初始化为 1,默认 0 ,无法乘
for(int i =0; i < cnt; i++)
for(int j = 0; j < sum[i]; j++)
multi(primes[i]);// 全局 res 乘上 每一个prime
// 结果输出
for(int i = res.size()-1; i >=0;i--)
{
System.out.print(res.get(i));
}
}
14. 卡特兰数
✨ 题目传送门
✨ 核心公式:C(2n,n) /(n+1) 【C是组合数】
static int mod = (int) 1e9 + 7;
// 快速幂求逆元,模p 必须为质数
static int qmi(int a, int k, int p)
{
int res = 1;
while (k > 0)
{
if ((k & 1) == 1)
res = (int) ((long) res * a % mod);
a = (int) ((long) a * a % mod);
k >>= 1;
}
return res;
}
public static void main(String[] args)
{
int n = 3;// 假装是输入的测试数据
int a = 2 * n;
int b = n;
int res = 1;
// 求 :A[b][a]
for (int i = a; i >= a - b + 1; i--)
res = (int) ((long) res * i % mod);
// 求b!
for (int i = b; i >= 1; i--)
res = (int) ((long) res * qmi(i, mod - 2, mod) % mod);
// 再除以 n+1 == 乘以 n+1 的逆元
res = (int) ((long) res * qmi(n + 1, mod - 2, mod) % mod);
System.out.println(res); // 输出 5
}
15. 容斥定理
✨ 容斥原理
✨ 参考传送门
✨ 求能被整除的数
static int N = 20, n, m;
static int[] p = new int[N];// 质数数组
public static void main(String[] args)
{
n = 10;// 被除数
m = 2; // m 个除数 p
p[0] = 2;
p[1] = 3;
// 输出 7
int res = 0;
// 遍历从 1 ~ 2^n-1
// 2^n == 1左移 m 位
for (int i = 1; i < 1 << m; i++)//这里的每一个 i 都代表着一种方案
{
int t = 1;// 质数的乘积
int s = 0;// 选了几个集合
// 这里是解析 i 方案对应的质数,二进制 1 代表有这个质数因子
for (int j = 0; j < m; j++)
{
if ((i >> j & 1) == 1)
{
if ((long) t * p[j] > n)
{
t = -1;
break;
}
t *= p[j];
s++;
}
}
if (t != -1)
{
if (s % 2 == 1)
res += n / t;
else
res -= n / t;
}
}
System.out.println(res);
}
16. 博弈论
(1)nim游戏
✨ 传送门
✨ 核心:
所有数按位与(^)== 0,先手必败
否则,先手必胜文章来源:https://www.toymoban.com/news/detail-860348.html
/*
先手必胜状态:先手操作完,可以走到某一个必败状态
先手必败状态:先手操作完,走不到任何一个必败状态
先手必败状态:a1 ^ a2 ^ a3 ^ ... ^an = 0
先手必胜状态:a1 ^ a2 ^ a3 ^ ... ^an ≠ 0
*/
public static void main(String[] args)
{
int n = 2;
int x1 = 1;
int x2 = 1;
// 输出必败 No
int res = 0;// 0 ^ x = x
// for(int i = 0; i < n; i++)
// {
// res ^= x;
// }
res = res ^ x1 ^ x2;
if (res == 0)
System.out.println("No");
else
{
System.out.println("Yes");
}
}
(2)集合Nim游戏
🙈 参考传送门
🙈 mex函数: 设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算,即:mex(S)= min(x]x属于自然数,且x不属于S。例:mex({0,1,3})= 2;
🙈 sg函数:根据终点态 sg(终点)= 0 逆推出每个节点的态文章来源地址https://www.toymoban.com/news/detail-860348.html
static int M = 110, N = 10010, k;
static int s[] = new int[M]; // 数字集合(每次可取多少颗石子)
static int sg[] = new int[N]; // 存放某个数的SG函数的值
public static void main(String[] args)
{
/*输入案例,输出 Yes
2
2 5
3
2 4 7
*/
Arrays.fill(sg, -1);
Scanner sc = new Scanner(System.in);
k = sc.nextInt(); // k代表数字集合里有多少个数
for (int i = 0; i < k; i++)
{
s[i] = sc.nextInt();
}
int n = sc.nextInt();//
int res = 0;
while (n-- > 0)
{
int x = sc.nextInt();
// 直接异或sg函数的和 进行判断
res ^= sg(x);
}
System.out.println(res != 0 ? "Yes" : "No");
}
// 递归 sg 有点难搞 debug看看
static int sg(int x)
{
if (sg[x] != -1)
return sg[x]; // 若sg存在直接返回出来
// 每次递归新创建一个set集合,便于求最小自然数
HashSet set = new HashSet<>();
// 枚举集合中每一个数 进行比较
for (int i = 0; i < k; i++)
{
if (x >= s[i])
{
// 取了 s[i] 个石子的方案
set.add(sg(x - s[i])); // 递归往set集合中添加sg函数
}
}
// 在集合中找,最小的不存在的值
for (int i = 0; i <= N; i++)
{
if (!set.contains(i))
{
return sg[x] = i;// 找到,保存,返回
}
}
return 0;
}
到了这里,关于搜索+图论+数论的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




![[数据结构]-二叉搜索树](https://imgs.yssmx.com/Uploads/2024/02/718431-1.png)




