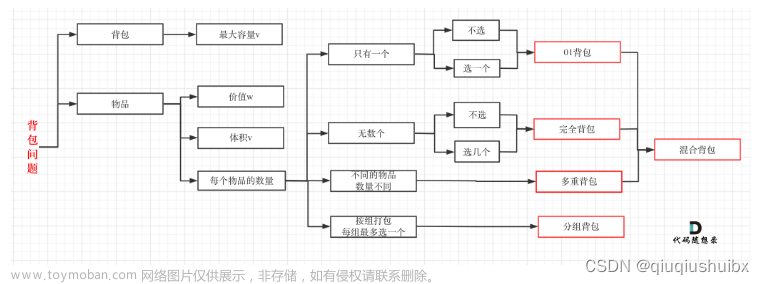
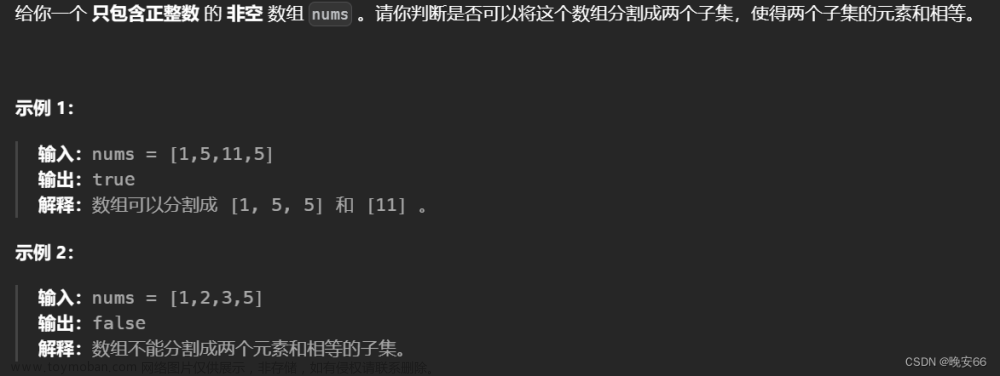
组合数问题
我们思考一下,如果要把数组分割成两个子集,并且两个子集的元素和相等,是否等价于在数组中寻找若干个数使之和等于所有数的一半?是的!
因此我们可以想到,两种方式:
①回溯的方式找到target,但是回溯是阶乘级别的算法,这里会超时。
②从前往后遍历,形象说明:定义n个集合dp[i],dp[i]表示前i个数的可能组合值,则有dp[i]={dp[i-1],dp[i-1]+i},dp[i-1]+i指的是i加上dp[i-1]中的所有元素得到的集合。同时由于长度最长200,数值最大为100,因此数的范围最大为1<=i<=20000,因此最多只有20000个不同的数。因此dp最大为2W个数!所以我们可以用集合实现,并且时间复杂度满足要求O(nums.length*nums.length*max(nums[i]))!
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=0;
for(auto &i:nums) sum+=i;
if(sum&1||nums.size()==1) return false;//只有偶数总和可以
sum>>=1;
unordered_set<int> Set;
vector<int> temp;
for(auto &i:nums){
if(i==sum) return true;
for(auto it=Set.cbegin();it!=Set.cend();++it){
int cur=*it+i;
if(cur==sum) return true;
if(cur<sum) temp.emplace_back(cur);//>sum的没意义
}
for(auto & j:temp) Set.insert(j);
temp.clear();
Set.insert(i);
}
return false;
}
};遇到的问题:
在循环遍历的过程中往容器中插入元素会导致容器迭代器end()和size(),时刻发生变化。与此同时,有的容器比如vector和string,往后面增加元素超过容量capacity可能会导致拷贝,从而整个迭代器失效。因此!在使用循环并且需要添加元素时,想使用迭代器需要额外注意!


比如本题是先将所需增加的放入到一个vector中的。
我们不能企图使用临时“指针”迭代器i=end(),然后遍历到it!=i,这是错误的!因为end()可能失效,而不是end()当时指向的位置。以下是C++ prime中特地提到的(这么小,但又特别灾难的坑被遇到了)
int tmp=Set.size(); for(auto it=Set.cbegin();tmp!=0;++it,--tmp){ int cur=*it+i; if(cur==sum) return true; temp.emplace_back(cur); Set.insert(cur); }这样做仍然是错误的,实际上我们在往非顺序容器中插入元素时,容器的数据结构会发生变化,因此导致++it可能并非按照原来的想法遍历,所以是错误的!
唯一正确且安全的方式是,如果需要在遍历的时候同时添加元素,最好不要使用迭代器!迭代器可以很好的遍历元素或者按迭代器范围赋值。但是边添加边遍历问题非常大。
因此对于无序容器只能使用迭代器的情况下,使用临时容器存储是非常必要的;对于顺序容器可以使用下标的情况下,使用下标更好。
动态规划
这道题实际上和0-1背包问题很像,即从n个物品中拿出一部分使得其值刚好等于target。意识到这一点我们可以定义动态转移方程:
dp[i][k]=max(dp[i-1][k-nums[i]],dp[i-1][k]);
dp[0][nums[0]]=1;
//dp[i][k]表示拿前i个物品是否可以达到重量k。
这实际上和方法一组合数问题是异曲同工的,方法一使用集合实现,那么如果方法一使用的是数组实现呢?那么数组中标记为1的实际上就是方法二的状态了!文章来源:https://www.toymoban.com/news/detail-860549.html
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=0;
for(auto &i:nums) sum+=i;
if(sum&1||nums.size()==1) return false;
sum>>=1;
vector<vector<int>> dp(nums.size(),vector<int>(sum+1,0));//超过sum实际上就不用看了
if(nums[0]<=sum)
dp[0][nums[0]]=1;
for(int i=1;i<nums.size();++i){
for(int j=1;j<=sum;++j){
dp[i][j]=dp[i-1][j];
if(j-nums[i]>=0)
dp[i][j]=max(dp[i-1][j-nums[i]],dp[i-1][j]);
}
if(nums[i]<=sum)
dp[i][nums[i]]=1;
}
return dp[nums.size()-1][sum];
}
};由于只用到前面的值,很显然我们可以降维优化。文章来源地址https://www.toymoban.com/news/detail-860549.html
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=0;
for(auto &i:nums) sum+=i;
if(sum&1||nums.size()==1) return false;
sum>>=1;
vector<int> dp(sum+1,0);//超过sum实际上就不用看了
if(nums[0]<=sum)
dp[nums[0]]=1;
for(int i=1;i<nums.size();++i){
for(int j=sum;j>=nums[i];--j){
dp[j]=max(dp[j],dp[j-nums[i]]);
}
}
return dp[sum];
}
};到了这里,关于力扣hot100:416.分割等和子集(组合/动态规划/STL问题)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!