【python库学习】 sklearn中的决策树Decision Trees-Toy模板网

这篇具有很好参考价值的文章主要介绍了【python库学习】 sklearn中的决策树Decision Trees。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、原理

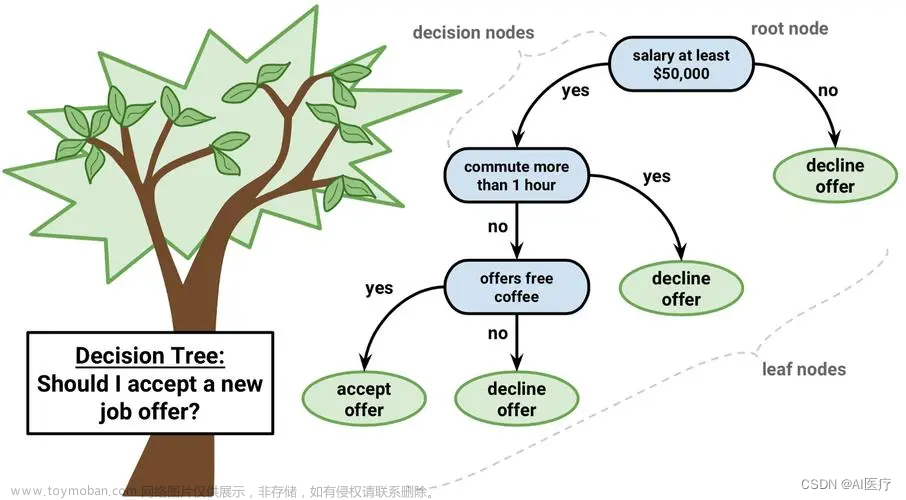
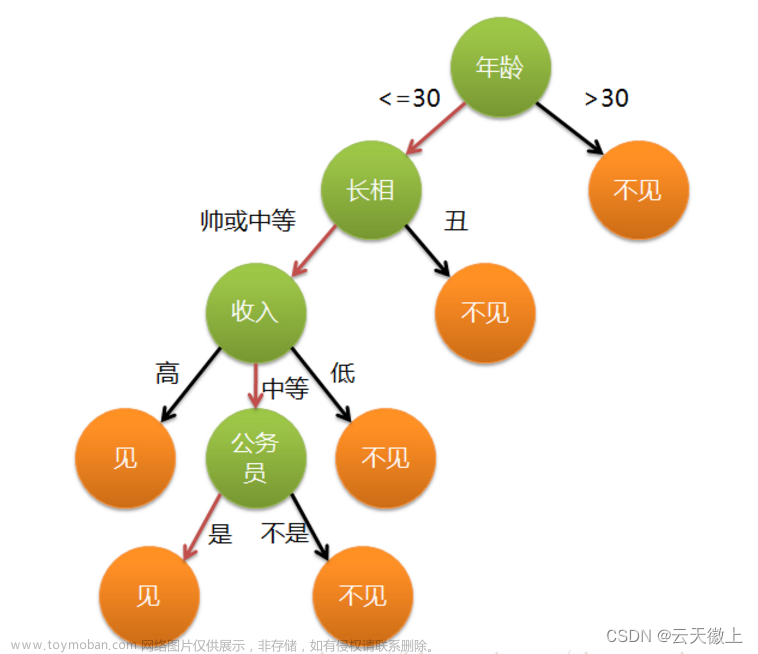
一棵决策树包含一个根结点、若干个内部结点和若干个叶结点;叶结点对应于决策结果,其他每个结点则对应于一个属性测试;每个结点包含的样本集合根据属性测试的结果被划分到子结点中;根结点包含样本全集.从根结点到每个叶结点的路径对应了一个判定测试序列.
sklearn 决策树,决策树,python,机器学习

划分准则
决策树构建的关键是每个节点的划分准则,常用的划分准则有信息增益,信息增益率,基尼指数.
假定当前样本集合 D中第k 类样本所占的比例为 Pk,其信息熵定义如下,信息熵越小,D的纯度越高:
$Ent(D)=-\displaystyle\sum_{k=1}^{|y|}(p_klog_2p_k)$
由此通过划分,划分后的信息熵与划分前的信息熵差,其差为信息增益,增益越大,说明划分结果越纯.其信息增益如下,a为划分属性,V为a属性下的不同取值数. $Gain(D,a)=Ent(D)-\displaystyle\sum_{v=1}^{V}{{|D^v| \above {1pt}|D| }Ent(D^v)}$
实际上，信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，加入了对每个属性取值数进行归一化的处理,加入该处理的结果称为信息增益率,具体公式如下:

需注意的是，增益率准则对可取值数目较少的属性有所偏好,因此 C4.5 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的.
基尼指数
剪枝
决策树剪枝是为了防止过拟合而对决策树进行优化的方法。决策树的剪枝可以分为预剪枝和后剪枝两种方法。
预剪枝(Pre-pruning)：在构造决策树的过程中，在节点划分之前，先对当前节点进行评估，如果该节点的划分不能带来决策树泛化性能的提升，那么该节点就不会被划分，直接作为叶子节点结束。
后剪枝(Post-pruning)：在决策树生成完全后，通过对整棵树进行自下而上的剪枝，将一些叶子节点替换成父节点，从而简化决策树的结构。后剪枝的常用方法是使用验证集进行评估，通过计算剪枝前后的预测准确率差异，若剪枝后的预测准确率上升则将剪枝后的节点作为叶节点。
两个方法的差异在,预剪枝容易造成欠拟合,因为常发生当前划分点没有提升性能,然在后续划分中有提升;后剪枝是需要先生成一颗完整复杂的决策树后再进行剪枝,其计算量较大.
在经典的CART树剪枝中,采用的就是后剪枝的方法,先生成一个最复杂的树，然后跟逐次剪掉最弱联系（衡量准则如误差发生变化时对应的最小复杂度）的树,直到只剩最后一个终结点。然后按一定准则（如测试集检测，K折交叉验证或者一个标准差准则）在一系列剪枝后的树里选择最优树作为剪枝后的输出。
缺失值处理
(1) 如何在属性值缺失的情况进行划分属性选择?
c4.5用了以下方案:
该方法的关键是采用对应特征非缺失值样本计算划分准则,并采用缺失权重进行矫正.
如属性A有缺失,则在待划分节点重新计算属性A信息熵1(采用剔除缺失后样本),然后计算属性A下的非缺失取值的信息熵2,缺失信息增益=信息熵1-信息熵2权重2,其中权重2等于属性A下某取值样本数➗(总非缺失值值样本数);最终信息增益=缺失信息增益权重1,其中权重1为总非缺失值值样本数➗总样本数.
(2) 缺失样本如何划分到子节点中?
同样的关键是赋予权重,非缺失样本权重均为1,缺失的样本同时放入该节点产生的所有子节点中,并赋予权重2.
连续值处理
采用离散方法进行处理,如c4,5用的是二分法,对连续值排序后,取两个连续值中间值作为划分点,计算增益.连续值特别的是在该节点得到最佳划分点划分后,还能在后面的子节点继续作为候选特征进行划分,区别是取值为上一节点划分后的子区间.

二、常见类型

常用的决策树类型包括：

ID3决策树：一种最早被提出的决策树算法，使用信息增益来选择特征。
C4.5决策树：ID3决策树的改进版本，使用信息增益率来选择特征。
CART决策树：以Gini指数或基尼系数为划分准则，既可以用于分类问题，也可以用于回归问题。是一种二叉树.
CHAID决策树：它是一种多叉树，可以用于分类和回归分析。树中每个节点都是一个特征，并通过卡方检验来确定每个特征的分裂点。通过计算每个分裂点的卡方值，选择卡方值最大的特征作为当前节点的分裂特征，然后将数据集根据该特征的不同取值分裂成多个子节点。
CHAID决策树的主要优点是能够处理分类变量和连续变量，且可适应多叉树结构。
首先，它对变量的多样性较为敏感，因此在处理高维度或者特征较多的数据时可能容易过拟合。
此外，CHAID决策树在处理缺失值时需要进行数据填充，处理不完整的数据可能会影响结果的准确性。
MARS决策树：多自适应回归样条（Multivariate Adaptive Regression Splines），主要用于回归问题。MARS决策树节点的划分首先选择最重要的特征，然后使用样条函数插值确定划分点完成的。通过将数据划分为不同的子空间，拟合局部线性模型，MARS决策树能够适应非线性关系和高维度特征。对计算资源的需求较高,对异常值较敏感.
节点的划分是通过以下两个步骤完成的：
特征选择（Feature Selection）：MARS决策树使用一种称为逆向逐步建模（Backward stepwise modeling）的方法来选择特征。首先，将所有特征视为自变量构建回归模型,计算每个特征的评估指标(如t值)。然后，剔除最不重要的特征(如t值小于阈值)，重新构建回归模型,直到满足迭代停止条件,最终剩余的特征为重要特征。
插值（Interpolation）：在选择了划分特征之后，对每一个划分点进行二分,使用样条函数（splines）来拟合子区间的局部线性关系。通常使用最小二乘法来拟合样条函数，选择使残差平方和最小化的划分点为最佳的划分点。

三、优缺点

优点

根据树结构可以得到数据更多的洞察,可解释性强
无需要求对数据进行标准化,空值处理
可以同时应用分类特征与连续特征
对异常点容错性强
支持分类任务,回归任务,多输入多输出任务
拟合时间复杂度是0（logN) N为样本数.

缺点

一是不加限制会学到复杂的树结构，需要注意控制过拟合问题；
二是样本稍微变动,决策树结构就会发生变化,不太稳定，通过集成学习可以得到一定的缓解；
三是决策树的决策边界是非顺滑非连续的，这个特点使得它较难扩展；
四是决策树的构建原理是采用启发式算法如贪婪算法在单个节点上优化，这点得到的决策树可能不是全局最优的拟合，该问题同样可以通过集成学习得到缓解；
五是决策树会偏向某些样本比例大的特征,在面对不平衡的数据集，决策树偏差会比较大，建议训练前进行数据平衡处理；
最后决策树的构建原理使得它对一些特别的情况难以拟合，如异或关系。

四、sklearn.tree

本库的决策树通过分段常数逼近目标分布，深度越大，其分段越细致，同时复杂度越大，拟合越好，过拟合风险上升。决策树易于理解与解释，且生成的决策树可以可视化；无需做数据标准化处理，空值剔除等，注意的是本库不支持缺失值；其拟合时间复杂度是0（logN) N为样本数；可以处理多输出问题，可以同时接受连续值与类别型数据，注意本库不支持类别型数据；对数据假设要求不严格，在部分违反下，表现仍然不错。当然根据决策树的原理，也有一些缺点，一是不加限制会学到复杂的树结构，需要注意控制过拟合问题；二是决策树不太稳定，通过集成学习可以得到一定的缓解；三是决策树的预测是非顺滑非连续的，这个特点使得它较难扩展；四是决策树的构建原理是采用启发式算法如贪婪算法在单个节点上优化，这点得到的决策树可能不是全局最优的拟合，该问题同样可以通过集成学习得到缓解；五是在面对不平衡的数据集，决策树偏差会比较大，建议训练前进行数据平衡处理；最后决策树的构建原理使得它对一些特别的情况难以拟合，如异或关系。

sklearn 决策树,决策树,python,机器学习

分类器

本库的使用方法如下方代码示例显示，其拟合预测操作模式保持sklearn的经典方式，拟合好的树可以绘制下方形式，也可以输出txt的格式；若要更生动的树展示，或者输出为pdf格式的树，则需要借助额外的库，通过conda install python-graphviz或者pip install graphviz安装，使用方法见第二段代码示例。

>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> from sklearn.tree import export_text
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)
>>> clf.predict([[2., 2.]]) #输出类别预测结果
>>> clf.predict_proba([[2., 2.]]) #输出各类别预测的概率
>>> tree.plot_tree(clf) #绘制决策树
>>>  #输出txt格式的决策树
>>> r = export_text(clf, feature_names=iris['feature_names'])
>>> print(r)
|--- petal width (cm) <= 0.80
|   |--- class: 0
|--- petal width (cm) >  0.80
|   |--- petal width (cm) <= 1.75
|   |   |--- class: 1
|   |--- petal width (cm) >  1.75
|   |   |--- class: 2

sklearn 决策树,决策树,python,机器学习

# 可以对树输出进行个性化设置
>>> dot_data = tree.export_graphviz(clf, out_file=None, 
...                      feature_names=iris.feature_names,  
...                      class_names=iris.target_names,  
...                      filled=True, rounded=True,  
...                      special_characters=True)  
>>> graph = graphviz.Source(dot_data) 
>>> graph.render("iris")  #输出pdf文件
>>> graph

回归

其调用方法如下代码，不再细说。

>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])

多输出问题

针对多输出的问题最直观的想法是，针对单个输出独立建模。但是实际中，多维输出之间可能存在相关性，因此可以选择拟合一个同时输出多维目标值的模型，这样更短的训练时间（只需要训练一个模型），而且表现上通常优于单个输出独立建模的方式。本库决策树通过改变下面两点实现多输出拟合：
1.叶结点上存储n维输出而不是1维
2.在树分裂时对n维输出计算评判标准，然后取平均作为最终分裂判断标准
在遇见多输出时，前面的分类与回归方法均支持，目标输入由 (n_samples,)变为 (n_samples, n_outputs)，使用方法与1维的类似，不再细谈。

时间复杂度

根据决策树的构建原理，容易得到一个节点，对每个个特征计算最佳评判标准值，需要计算N_features次，计算一个特征的一个分割点的评判标准值为O(N_samples)，计算一个特征最佳分割点需要计算log(N_samples)次的评判标准值，因此构建一个节点需要O(N_featuresN_sampleslog(N_samples))，构建一棵树为O(N_featuresN_samples^2log(N_samples)).当树是均衡的二叉树时，其时间复杂度为O(N_featuresN_sampleslog(N_samples))+log(N_samples)。

实际应用注意点

参数列表

共12个参数

参数名	含义	应用说明
criterion	判定准则	{“gini”, “entropy”, “log_loss”},该库中实现的是CART树,因此默认”gini”
splitter	节点划分策略	{“best”, “random”},默认”best”
max_depth	树深	默认”None”,应用见4,不设置则持续分裂到最低阈值(见应用6)
min_samples_split	最小分割样本量	默认2,可设置为整数或者小数,整数为样本数,小数为输入样本比例
min_samples_leaf	最小叶结点样本量	默认1,用法同min_samples_split
min_weight_fraction_leaf	最小叶结点样本权重	默认0,为叶结点样本权重总和,应用见6点
max_features	节点划分最大特征集数	int, float or {“auto”, “sqrt”, “log2”}, default=None,其中小数为特征数比例
random_state	随机状态	主要用于在选择候选特征时,设置后提高划分的一致性
max_leaf_nodes	最大叶结点数	int, default=None,建议根据非纯度下降情况进行设置
min_impurity_decrease	划分非纯度最小下降值	float, default=0.0,设置后对结点是否能分裂添加纯度提升阈值判定,小于阈值不进行结点分裂
class_weight	类权重	dict, list of dict or “balanced”, default=None,对多类分类时,接受[{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] 输入而不是[{1:1}, {2:5}, {3:1}, {4:1}].
ccp_alpha	最小成本计算复杂度剪枝参数	non-negative float, default=0.0,见最小成本计算复杂度剪枝内容

树对有大量特征的情况下容易过拟合，因此注意样本数与特征数的比例，样本数少维度高的时候容易过拟合
可以考虑在树拟合前进行降维处理（PCA, ICA, or Feature selection），这样树拟合的时候找到有区别的特征的几率更大
理解树的结构有助于在树做预测时获得更多的洞察，这对数据特征重要性的理解很重要
在首次拟合树时，可以设置最大深度为3，输出树的拟合样子，有助于理解模型是如何拟合数据集的；然后再逐步加深树
记住树每加深一层，所需样本数翻倍，根据该点去限制最大深度预防过拟合
使用参数 min_samples_split （最小分割样本量）或者min_samples_leaf （最小叶结点样本量）防止过拟合；在大型数据集下，可以尝试设置 min_samples_leaf=5；这两个参数的差别在于前者可以得到任意样本数的叶结点，后者确保每一个叶结点样本数的下限，这避免了在回归任务中的出现过拟合，低方差的叶结点；在分类任务中通常设置 min_samples_leaf=1；当样本带有样本权重时，考虑设置参数min_weight_fraction_leaf 或者 min_impurity_decrease 。
在数据不平衡的场景下，建议在训练前对训练集进行数据平衡处理，如从每类中采样同样数量的样本，或者将每个类的样本权重之和归一化为相同的值；注意使用基于权重的预剪枝min_weight_fraction_leaf参数，得到的树模型偏差要小于非权重的预剪枝 min_samples_leaf。
本库所有决策树采用的是np.float32数据集，如果训练集不是该类型，将对训练集生成副本。这在大型数据集下需要考虑空间资源的问题。
如果训练集X非常稀疏，建议在拟合前转化为稀疏的csc_matrix矩阵，在预测前将预测集转化为csr_matrix矩阵，如此在有许多样本中含0 的场景下，使用稀疏矩阵训练可以快几个数量级。

树算法ID3, C4.5, C5.0 and CART

本库实现的是CART树

ID3是多分枝树，每个节点基于分类型目标计算分类型特征的最大信息增益得到分割点，树先构建到最大尺寸，然后进行后剪枝操作。
C4.5相比于ID3，取消了特征必须是分类型的限制，对于数值型特征采用分段离散的方法进行处理；采用的是信息增益率而非信息增益考虑到了特征差异值较多信息增益天然高的问题。C4.5将训练好的树转化为if else的规则集，然后按顺序对每条规则进行验证，当去除该条规则，准确度上升则删除该条规则（类似后剪枝）。
C5.0在C4.5的基础上使用内存更小，产出的规则集更小，准确度更高。
CART树构造二叉树，支持数值型的目标变量，分类任务使用基尼指数进行构造，回归时采用平方误差进行构造；不会计算规则集。

最小成本计算复杂度剪枝

其原理可以参考这篇文章CART树剪枝，总的原理是代价，复杂度，与剪枝间的关系，代价是每个叶结点错误分类的权重均值 $R (T)$ ；复杂度由参数 $\alpha$ 进行控制，按照下方公式进行复杂度计算；剪枝则为将非叶结点做为叶结点，这样该结点后面的部分被丢弃；这样每一次剪枝对应一个新的复杂度（通过下方包含了代价与复杂参数的公式计算）。
sklearn 决策树,决策树,python,机器学习
总的剪枝流程是，先生成一个最复杂的树，然后跟逐次剪掉最弱联系（复杂度发生变化时对应最小的 $\alpha$ ）的树,直到只剩最后一个终结点。然后按一定准则（如测试集检测，K折交叉验证或者一个标准差准则）在一系列剪枝后的树里选择最优树作为剪枝后的输出。文章来源地址https://www.toymoban.com/news/detail-860555.html