6自由度并联机器人 运动学算法 正解 逆解
6个耦合的非线性方程组求解
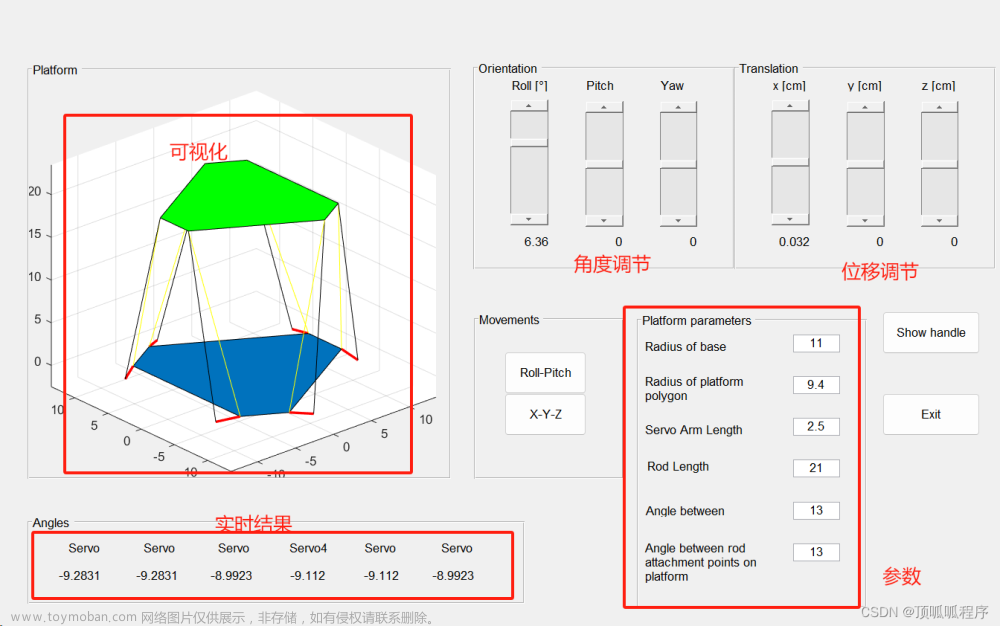
正解快速收敛可用在机器人控制中
已实际使用
6自由度并联机器人运动学算法及其在机器人控制中的应用
随着社会科技的不断发展,机器人技术在工业自动化和服务业中的应用越来越广泛。其中,高自由度并联机器人作为一种重要的机器人类型,受到了广泛的关注。本文将围绕6自由度并联机器人的运动学算法展开讨论,特别是正解和逆解的求解方法。
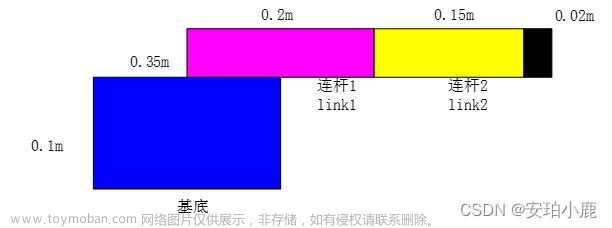
首先,我们要理解什么是6自由度并联机器人。简单来说,6自由度并联机器人是指机器人有6个自由度,即6个独立的运动变量,可以在空间中完成各种姿态的运动。与传统的机器人相比,6自由度并联机器人更加灵活和高效,并且适用于各种环境。
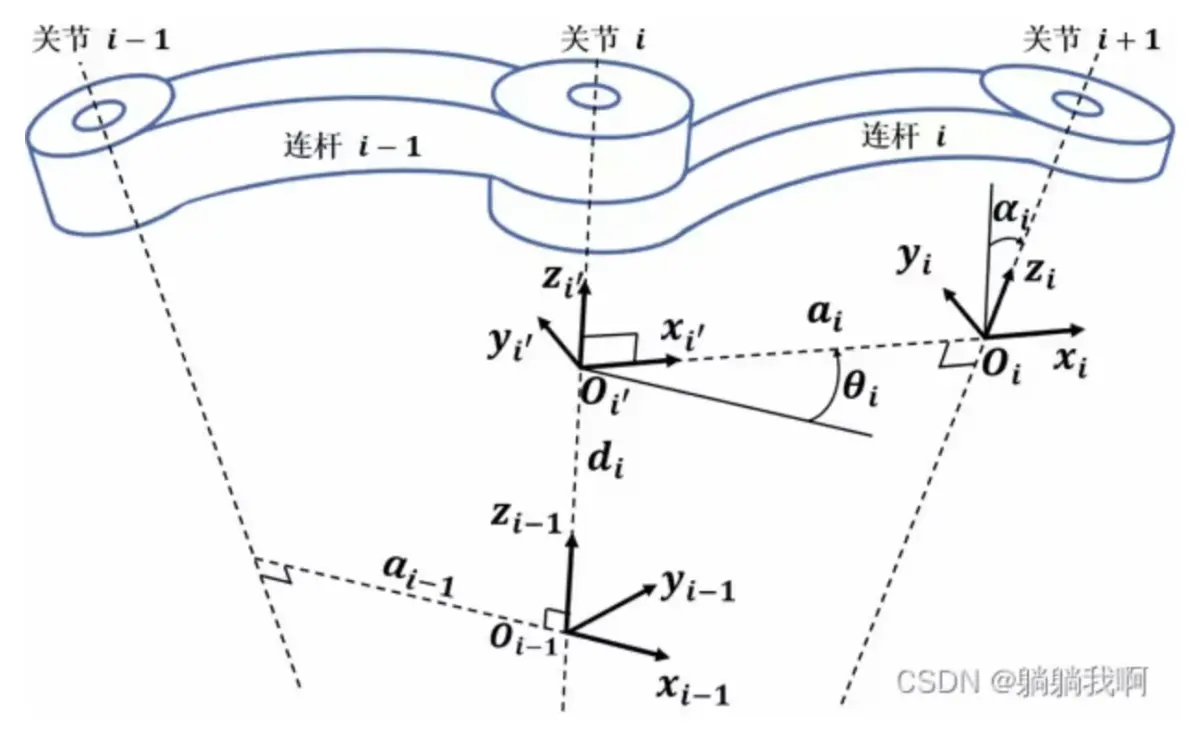
在控制6自由度并联机器人时,运动学算法是一个很关键的部分。运动学算法可以将机器人的姿态和位置进行精确计算和控制。在6自由度并联机器人中,运动学算法的基本任务是确定机器人各个执行器的角度和位置,从而达到人机交互和自动化控制的目的。
关于6自由度并联机器人的运动学算法,最常见的问题是正解和逆解问题。正解问题是在已知机器人各个执行器的角度和位置时,确定机器人的姿态和位置。逆解问题是在已知机器人的姿态和位置时,确定机器人各个执行器的角度和位置。在实际控制中,正解和逆解问题都需要求解,因此,运动学算法的求解方法非常重要。
对于6自由度并联机器人的正解问题,可以使用解析法、数值法或混合法进行求解。其中,解析法是将机器人的位姿方程简化成一组代数方程,通过求解代数方程组来获得解。数值法则通过数值计算方法来近似求解位姿方程。混合法则是将解析法和数值法相结合,实现更好的数值精度和求解速度。在实际应用中,选择不同的方法取决于机器人的结构、运动范围和计算需求等因素。
对于6自由度并联机器人的逆解问题,可以使用牛顿迭代法、遗传算法或线性化迭代方法进行求解。其中,牛顿迭代法是最常见的算法之一,它将机器人的逆运动学问题转化成非线性方程组的求解问题。具体地说,首先计算机器人的雅各比矩阵,然后使用牛顿迭代法来求解非线性方程组。牛顿迭代法具有求解速度快、收敛性好等特点,是实际控制中常用的方法之一。
在上述逆解算法中,非线性方程组的求解是一个关键的环节。在6自由度并联机器人的逆解问题中,通常需要求解6个耦合的非线性方程组。这些方程组是非线性、多元且复杂的,因此求解难度很大。对于这些方程组的求解,可以使用数值计算方法、近似计算方法或符号计算方法等多种方法,具体方法的选择需要考虑计算效率和精度等因素。
结论
综上所述,6自由度并联机器人的运动学算法是机器人控制中的一个重要问题。正解和逆解求解方法的选择对机器人的控制精度和效率有着重要的影响。在实际应用中,需要根据具体情况选择不同的算法和方法,以实现机器人的优化控制。已实际使用的算法应该在进一步的实践中得到验证和完善,以确保它的效果和可靠性。文章来源:https://www.toymoban.com/news/detail-860635.html
相关代码,程序地址:http://lanzouw.top/681126954454.html
文章来源地址https://www.toymoban.com/news/detail-860635.html
到了这里,关于6自由度并联机器人 运动学算法 正解 逆解6个耦合的非线性方程组求解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!