文章目录
一、前言
二、FFT是什么(原理)?
三、FFT IP核参数介绍
四、仿真
0、文件完整结构
1、设置IP核
2、例化FFT,并完善顶层文件
3、利用matlab生成正弦波信号
4、导出变量x生成的正弦波数据
5、编写testbench
6、RTL Simulation
五、上板
1、matlab生成正弦波信号并导出mif文件
2、ram ip核设置及相关模块
ram_ip例化(简单驱动)
ram_rw(读写控制)
fft_ram(连接fft和ram)
3、fft ip核
4、计算频谱下标
5、上板验证(signaltap)
六、IP核破解
参考文献及资料
总结
一、前言
注意:笔者使用的是Quartus Standard 17.1版本,高版本的Quartus需要先破解IP核才能调用FFT,不然在编译仿真时会在EDA Netlist Writer报错说没有相应的license,同时打开simulation tool也会报错。板子用的是小梅哥的AC620V2开发板,型号是cyclone IV E : EP4CE10F17C8。
二、FFT是什么(原理)?
FFT(快速傅里叶变换)是数字信号处理中一种重要的算法,用于将一个信号从时域转化为频域。其原理基于傅里叶变换,但相比传统的傅里叶变换,FFT算法具有更高的计算效率。
FFT算法的原理是将一个N点的离散信号通过递归分治的方式分解成多个小规模的离散信号,然后通过频域旋转因子的运算将其合并成最终的频域结果。具体而言,FFT算法通过将信号分解为偶数点和奇数点,然后再对这些小规模的子问题进行傅里叶变换,最终将结果合并得到信号的频域表示。
FFT算法在数字信号处理中具有重要的意义。首先,FFT算法可以将信号从时域转换为频域,这使得我们可以了解信号的频谱特征,例如信号的频率成分、幅度和相位信息等。这对于信号处理、频谱分析和滤波等应用非常重要。
其次,FFT算法具有高效的计算速度。传统的傅里叶变换算法的计算复杂度为O(N^2),而FFT算法的计算复杂度为O(NlogN)。这意味着FFT算法能够在较短的时间内进行大规模信号的频域变换,对于实时信号处理和大数据处理具有重要意义。
此外,FFT算法还有其他一些重要的应用,例如信号滤波、频谱估计、相关性分析和频谱乘法等。这些应用使得FFT成为数字信号处理中必不可少的工具。
快速傅里叶变换的基本思想是将时域序列逐次分解为一组子序列,利用旋转因子的特性,由子序列的DFT来实现整个序列的DFT。
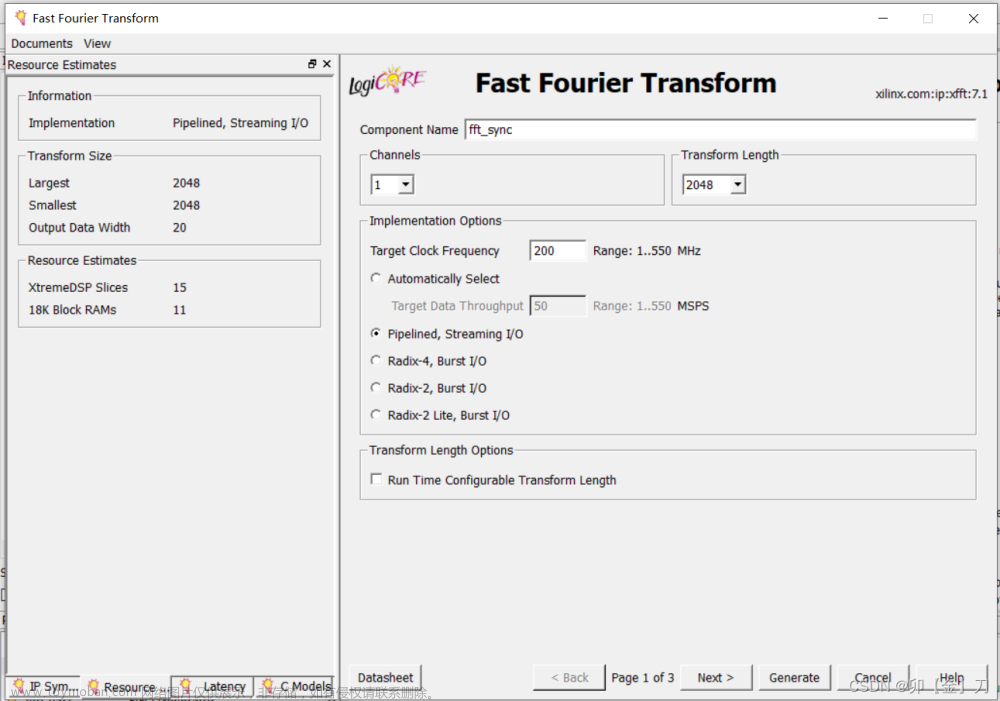
三、FFT IP核参数介绍
按以下步骤可以打开官方对于FFT IP核的解释文档
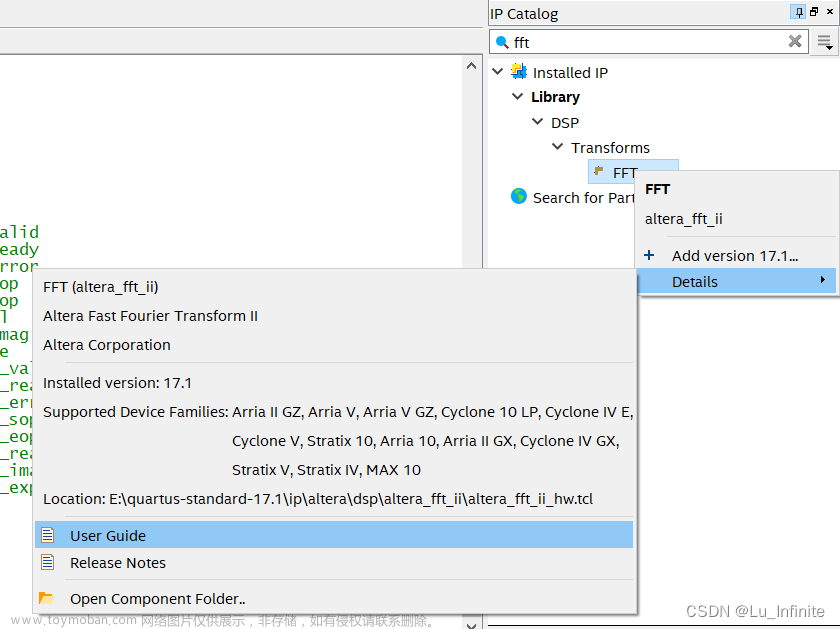
双击FFT可以进入IP核设置界面

Transform:Length是指转换序列长度或者在可变数据流模式下的最大转换长度;Direction可选FFT或者逆快速傅里叶变换IFFT。同时可以在端口信号inverse处设置变换方向,0为FFT,1为IFFT。
.inverse (inverse), // .inverseI/O:Data Flow可以选择四种模式Variable Streaming、Streaming、Buffered Burst、Burst。可以根据自己的需求选择具体的模式。Streaming模式允许对于输入数据的持续处理并且持续输出处理后的数据流,不需要暂停输入输出数据流。Variable Streaming模式和Streaming模式很相似,但Variable Streaming在FFT运行过程中可以处理不同长度的序列。Buffered Burst模式进行FFT的处理时间会相对久一点,但对于内存资源的需求会比Streaming模式少。Burst模式和Buffered Burst模式也很相似,但Burst会消耗更少的内存资源,同时平均吞吐量会更低。
Data and Twiddle:设置数据类型和旋转因子。和之前设置的IO模式有对应关系,否则会显示报错。可以再具体翻一翻手册。
| Parameters | Value | Description |
|---|---|---|
| Transform Length |
64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, or 65536. Variable streaming also allows 8, 16, 32, 131072, and 262144 |
The transform length. For variable streaming, this value is the maximum FFT length. |
| Transform Direction | Forward,reverse, bidirectional |
The transform direction. |
| I/O Data Flow | Streaming Variable Streaming Buffered Burst Burst |
If you select Variable Streaming and Floating Point, the precision is automatically set to 32, and the reverse I/O order options are Digit Reverse Order. |
| I/O Order | Bit Reverse Order, Digit Reverse Order, Natural Order, N/2 to N/2 |
The input and output order for data entering and leaving the FFT (variable streaming FFT only). The Digit Reverse Order option replaces the Bit Reverse Order in variable streaming floating point variations. |
| Data Representation | Fixed point or single floating point, or block floating point |
The internal data representation type (variable streaming FFT only), either fixed point with natural bit-growth or single precision floating point. Floating-point bidirectional IP cores expect input inThe internal data representation type (variable streaming FFT only), either fixed point with natural bit-growth or single precision floating point. Floating-point bidirectional IP cores expect input in |
| Data Width | 8, 10, 12, 14, 16, 18, 20,24, 28, 32 | The data precision. The values 28 and 32 are available for variable streaming only. |
| Twiddle Width | 8, 10, 12, 14, 16, 18, 20,24, 28, 32 | The twiddle precision. The values 28 and 32 are available for variable streaming only. Twiddle factor precision must be less than or equal to data precision. |
Basic Parameters
在Burst模式下还需要配置Advanced Parameters,但只需要配置FFT Engine Architecture和Number of Parallel FFT Engines。

| Parameters | Value | Description |
|---|---|---|
| FFT Engine Architecture | Quad Output, Single Output |
Choose between one, two, and four quad-output FFT engines working in parallel. Alternatively, if you have selected a singleoutput FFT engine architecture, you may choose to implement one or two engines in parallel. Multiple parallel engines reduce transform time at the expense of device resources, which allows you to select the desired area and throughput trade-off point. Not available for variable streaming or streaming FFTs. |
| Number of Parallel FFT Engines | 1, 2, 4 | |
| DSP Block Resource Optimization | On or Off | Turn on for multiplier structure optimizations. These optimizations use different DSP block configurations to pack multiply operations and reduce DSP resource requirements. This optimization may reduce FMAX because of the structure of the specific configurations of the DSP blocks when compared to the basic operation. Specifically, on Stratix V devices, this optimization may also come at the expense of accuracy. You can evaluate it using the MATLAB model provided and bit wise accurate simulation models. If you turn on DSP Block Resource Optimization and your variation has data precision between 18 and 25 bits, inclusive, and twiddle precision less than or equal to 18 bits, the FFT MegaCore function configures the DSP blocks in complex 18 x 25 multiplication mode. |
| Enable Hard Floating Point Blocks | On or off | For Arria 10 devices and single-floating-point FFTs only. |
在配置完IP后,可以看到生成的Block Symbol 。

具体信号含义可以看下表,帮助理解。该表来源于FPGA学习专题-FFT IP核的使用_quartus实现fft全流程-CSDN博客

在配置IP核时可以考虑fft的延时问题,burst模式比stream模式稍慢,而基4模式比基2模式(在advanced parameters中设置)快,可以搭配使用。

四、仿真
在matlab中生成正弦波,并将数据导入FPGA进行仿真,验证FFT核的正确性
0、文件完整结构
在后续建文件和修改绝对路径时尽量参考这个文件结构。


1、设置IP核
这是Quartus中FFT IP核的编辑界面。要generate两个地方,不然在仿真的时候会报错

2、例化FFT,并完善顶层文件
//File name:fft_demo
//Complete date:23/03/24
/
module fft_demo(
input wire clk,
input wire rst_n,
input wire sink_valid,
input wire sink_sop,
input wire sink_eop,
input signed [15:0] data_in,
output wire source_valid,
output wire source_sop,
output wire source_eop,
output signed [31:0] data_out
);
wire sink_ready;
wire [1:0] sink_error;
wire signed [15:0] sink_imag;
wire inverse;
wire source_ready;
wire [1:0] source_error;
wire signed [15:0] source_real;
wire signed [15:0] source_imag;
wire [5:0] source_exp;
assign sink_error=2'b00;
assign sink_imag=16'd0;
assign inverse=1'b0;
assign source_ready=1'b1;
fft u0 (
.clk (clk), // clk.clk
.reset_n (rst_n), // rst.reset_n
.sink_valid (sink_valid), // sink.sink_valid
.sink_ready (sink_ready), // .sink_ready
.sink_error (sink_error), // .sink_error
.sink_sop (sink_sop), // .sink_sop
.sink_eop (sink_eop), // .sink_eop
.sink_real (data_in), // .sink_real
.sink_imag (sink_imag), // .sink_imag
.inverse (inverse), // .inverse
.source_valid (source_valid), // source.source_valid
.source_ready (source_ready), // .source_ready
.source_error (source_error), // .source_error
.source_sop (source_sop), // .source_sop
.source_eop (source_eop), // .source_eop
.source_real (source_real), // .source_real
.source_imag (source_imag), // .source_imag
.source_exp (source_exp) // .source_exp
);
wire signed [31:0] dout_re,dout_im;
assign dout_re=source_real*source_real;
assign dout_im=source_imag*source_imag;
assign data_out=dout_re+dout_im;
endmodule
3、利用matlab生成正弦波信号
这段代码首先定义了采样频率fs为100000Hz,信号频率f1为1000Hz,然后生成了一个长度为2048的时间序列t,采样频率为fs。接着生成了一个长度为2048的信号x,信号是由0.5倍幅度的1000Hz正弦波和0.5的直流分量组成,然后将其量化为8位,即取值范围为0-255。
接下来使用fft函数对信号x进行1024点的快速傅里叶变换,得到频谱y。然后使用plot函数绘制了频谱y的幅度平方的图像,即频谱的能量谱图。
clc;
clear;
fs=100000;
f1=1000;
t=0:1/fs:2047/fs;
x=floor((0.5*cos(2*pi*f1*t)+0.5)*255);
plot(x);
y=fft(x,1024);
plot(abs(y).*abs(y));
4、导出变量x生成的正弦波数据
新建一个trans.cpp文件,将datain.txt中的数据导入dataset.vh文件。
#include<bits/stdc++.h>
using namespace std;
int main()
{
freopen("datain.txt","r",stdin);
freopen("dataset.vh","w",stdout);
signed short val;
for(int i=0;i<2048;i++)
{
cin>>val;
printf("%x\n",val);
}
fclose(stdin);
fclose(stdout);
return 0;
}5、编写testbench
注意要修改其中的路径,不然在仿真时会报错。
/
`timescale 1ns/1ns
module fft_demo_tb;
reg clk;
reg rst_n;
wire sink_valid;
wire sink_sop;
wire sink_eop;
wire signed [15:0]data_in;
wire source_valid;
wire source_sop;
wire source_eop;
wire [1:0]source_error;
wire signed [31:0]data_out;
parameter FILE_PATH="E:/Quartus-standard-17.1/Documents/fft/simulation/modelsim/dataset.vh";
reg [15:0] data[2048:0];
initial begin
clk=0;
$readmemh(FILE_PATH,data);
#0 rst_n=0;
#110 rst_n=1;
end
always #5 clk=~clk;
reg [10:0] cnt;
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)begin cnt<=0; end
else begin cnt<=cnt+1; end
end
assign data_in=data[cnt];
reg [10:0] cnt1;
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)begin cnt1<=0; end
else begin cnt1<=cnt1+1; end
end
assign sink_sop=(cnt1==1 && rst_n==1)?1:0;
assign sink_eop=(cnt1==1024 && rst_n==1)?1:0;
assign sink_valid=(cnt1>=1 && cnt1<=1024 && rst_n==1)?1:0;
fft_demo u_test(
.clk(clk),
.rst_n(rst_n),
.sink_valid(sink_valid),
.sink_sop(sink_sop),
.sink_eop(sink_eop),
.data_in(data_in),
.source_valid(source_valid),
.source_sop(source_sop),
.source_eop(source_eop),
.source_error(source_error),
.data_out(data_out)
);
integer vec_file1;
initial
begin
wait(rst_n==1'b1);
#10;
vec_file1=$fopen("E:/Quartus-standard-17.1/Documents/fft/data_out.dat","w");
forever
begin
@(posedge clk);
#1;
if(source_valid)
$fwrite(vec_file1,"%d\n",data_out);
end
$fclose(vec_file1);
end
endmodule
6、RTL Simulation
打开Quartus中的RTL Simulation。

可以从仿真图上看到source_valid为1期间,data_out结果即为fft之后的频谱结果。可以看到结果和matlab生成的效果相差无几。

五、上板
将matlab中生成的信号数据导成mif文件,FPGA 使用ram ip核读取mif文件,再调用fft ip核计算频谱。
1、matlab生成正弦波信号并导出mif文件
clc;
clear;
fs=800;
f1=50;
N=1024;
x=0.5*sin(2*pi*f1/fs*(0:N-1));
f_axis=[0:N-1]*fs/N;
figure;
plot(x); %原信号
y=fft(x,1024);
figure;
plot(f_axis,abs(y)); %频谱
% 将信号量化为12位
x_quantized = round(x * (2^11-1));
% 生成mif文件
fid = fopen('single_freq_signal.mif', 'w');
fprintf(fid, 'DEPTH = 1024;\n');
fprintf(fid, 'WIDTH = 12;\n');
fprintf(fid, 'ADDRESS_RADIX = HEX;\n');
fprintf(fid, 'DATA_RADIX = HEX;\n');
fprintf(fid, 'CONTENT\n');
fprintf(fid, 'BEGIN\n');
for i = 0:1023
fprintf(fid, '%03X : %03X;\n', i, x_quantized(i+1));
end
fprintf(fid, 'END;\n');
fclose(fid);2、ram ip核设置及相关模块

ram_ip例化(简单驱动)
//顶层模块
module ram_ip(
input sys_clk, //系统时钟
input sys_rst_n, //系统复位,低电平有效
output [7:0] ram_rd_data
);
//wire define
wire ram_wr_en ; //ram写使能
wire ram_rd_en ; //ram读使能
wire [9:0] ram_addr ; //ram读写地址
wire [7:0] ram_wr_data ; //ram写数据
//wire [7:0] ram_rd_data ; //ram读数据
ram_rw ram_rw_inst( //例化底层模块
.clk (sys_clk), //系统时钟
.rst_n (sys_rst_n), //系统复位,低电平有效
.ram_wr_en (ram_wr_en ), //ram写使能
.ram_rd_en (ram_rd_en ), //ram读使能
.ram_addr (ram_addr ), //ram读写地址
.ram_wr_data (ram_wr_data), //ram写数据
.ram_rd_data (ram_rd_data) //ram读数据
);
ram_config ram_config_inst ( //实例化底层IP核
.address (ram_addr), //ram读写地址
.inclock (sys_clk), //系统时钟
.outclock (sys_clk),
.data (ram_wr_data), //ram写数据
.rden (ram_rd_en), //ram读使能
.wren (ram_wr_en), //ram写使能
.q (ram_rd_data) //ram读数据
);
endmodule
ram_rw(读写控制)
//RAM读写驱动
module ram_rw(
input clk , //时钟信号
input rst_n , //复位信号,低电平有效
output ram_wr_en , //ram写使能
output ram_rd_en , //ram读使能
output reg [9:0] ram_addr , //ram读写地址
output reg [7:0] ram_wr_data, //ram写数据
output reg read_flag,
input [7:0] ram_rd_data //ram读数据
);
reg [10:0] rw_cnt ; //读写控制计数器
//rw_cnt计数范围在0~31,ram_wr_en为高电平;32~63时,ram_wr_en为低电平
//assign ram_wr_en = ((rw_cnt >= 6'd0) && (rw_cnt <= 6'd31)) ? 1'b1 : 1'b0;
assign ram_wr_en = 1'b0;
//rw_cnt计数范围在32~63,ram_rd_en为高电平;0~31时,ram_rd_en为低电平
assign ram_rd_en = ((rw_cnt >= 11'd0) && (rw_cnt <= 11'd1023)) ? 1'b1 : 1'b0; //assign赋值功能
//读写控制计数器,计数器范围0~63
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0)
rw_cnt <= 11'd0;
else if(rw_cnt == 11'd1023) //计数到63清零
begin
rw_cnt <= 11'd0;
read_flag<=1;
end
else //if(rw_cnt < 11'd1023)
begin
rw_cnt <= rw_cnt + 11'd1;
read_flag<=0;
end
end
//读写控制器计数范围:0~31 产生ram写使能信号和写数据信号
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0)
ram_wr_data <= 8'd0;
else if(rw_cnt >= 6'd0 && rw_cnt <= 6'd31)
ram_wr_data <= ram_wr_data + 8'd1;
else
ram_wr_data <= 8'd0;
end
//读写地址信号 范围:0~31
always @(posedge clk or negedge rst_n) begin
if(rst_n == 1'b0)
ram_addr <= 10'd0;
else if(ram_addr == 10'd1023)
ram_addr <= 10'd0;
else
ram_addr <= ram_addr + 1'b1;
end
endmodule
fft_ram(连接fft和ram)
module fft_ram(
input clk,
input rst_n,
output [15:0] data_out,
output source_valid
);
wire [7:0] ram_rd_data;
ram_ip ram_ip(
.sys_clk(clk),
.sys_rst_n(rst_n),
.ram_rd_data(ram_rd_data)
);
fft_demo fft_demo(
.clk(clk),
.rst_n(rst_n),
.data_in(ram_rd_data),
.data_out(data_out),
.source_valid(source_valid)
);
endmodule
3、fft ip核
ip核设置

//File name:fft_demo
//Complete date:23/03/24
/
module fft_demo(
input wire clk,
input wire rst_n,
input signed [7:0] data_in,
output signed [15:0] data_out,
output wire source_valid
);
wire sink_valid;
wire sink_sop;
wire sink_eop;
//wire source_valid;
wire source_sop;
wire source_eop;
wire [1:0] source_error;
wire sink_ready;
wire [1:0] sink_error;
wire signed [7:0] sink_imag;
wire inverse;
wire source_ready;
//wire [1:0] source_error;
wire signed [7:0] source_real;
wire signed [7:0] source_imag;
wire [5:0] source_exp;
assign sink_error=2'b00;
assign sink_imag=8'd0;
assign inverse=1'b0;
assign source_ready=1'b1;
reg [10:0] cnt;
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)
cnt<=0;
else
cnt<=cnt+1;
end
assign sink_sop=(cnt==1)?1:0;
assign sink_eop=(cnt==1024)?1:0;
assign sink_valid=(cnt>=1 && cnt<=1024)?1:0;
fft u0 (
.clk (clk), // clk.clk
.reset_n (rst_n), // rst.reset_n
.sink_valid (sink_valid), // sink.sink_valid
.sink_ready (sink_ready), // .sink_ready
.sink_error (sink_error), // .sink_error
.sink_sop (sink_sop), // .sink_sop
.sink_eop (sink_eop), // .sink_eop
.sink_real (data_in), // .sink_real
.sink_imag (sink_imag), // .sink_imag
.inverse (inverse), // .inverse
.source_valid (source_valid), // source.source_valid
.source_ready (source_ready), // .source_ready
.source_error (source_error), // .source_error
.source_sop (source_sop), // .source_sop
.source_eop (source_eop), // .source_eop
.source_real (source_real), // .source_real
.source_imag (source_imag), // .source_imag
.source_exp (source_exp) // .source_exp
);
wire signed [15:0] dout_re,dout_im;
assign dout_re=source_real*source_real;
assign dout_im=source_imag*source_imag;
assign data_out=dout_re+dout_im;
endmodule4、计算频谱下标
输出的fft结果只有单个单个的频点,但有时需要信号频率信息,即需要根据公式f=(k*fs)/N
//通过横坐标算出对应频率,其实也就是找峰值
module f_calculate(
input clk,
input rst_n,
output reg [15:0] peak_value,
output reg [9:0] peak_index,//未经过换算
output reg [9:0] peak_index2,//经过换算
output reg [9:0] index
);
reg [15:0] data_array [0:1023];
reg [15:0] fs=16000;
reg [15:0] threshold1=500;//设置上下阈值
reg [15:0] threshold2=2000;
wire [15:0] data_out;
wire source_valid;
fft_ram fft_ram_inst(
.clk(clk),
.rst_n(rst_n),
.data_out(data_out),
.source_valid(source_valid)
);
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
index<=0;
peak_value<=0;
peak_index<=0;
end
else begin
if(source_valid)
begin
data_array[index]<=data_out;
index<=index+1;
if(data_out>threshold1 && data_out<threshold2)
begin
peak_value<=data_out;
peak_index<=index<512 ? index : 1024-index;
peak_index2<=peak_index*fs/1024;
end
end
end
end
endmodule
5、上板验证(signaltap)
可以看到能正确显示对应频率。

六、IP核破解
如果使用的是高版本的Quartus需要先破解IP核才能调用FFT,不然在编译仿真时会在EDA Netlist Writer报错说没有相应的license。

参考文献及资料
1、丝滑仿真quartus fft ip_哔哩哔哩_bilibili (这个up主的视频里有仿真部分的完整操作,保姆级,强烈推荐)
2、FPGA学习专题-FFT IP核的使用_quartus实现fft全流程-CSDN博客
3、这篇博客介绍了使用modelsim的一些常见问题和解决办法
modelsim遇到的问题_illegal base specifier in numeric constant-CSDN博客 文章来源:https://www.toymoban.com/news/detail-861081.html
其他
以上就是完整使用fft ip核进行仿真和实际上板的过程。笔者学识尚浅,文章内容可能有些许纰漏。如有问题可指出,共同讨论学习。文章来源地址https://www.toymoban.com/news/detail-861081.html
到了这里,关于【FPGA】FFT测量信号频率(Quartus IP核)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!