【动态规划】之石子合并问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了【动态规划】之石子合并问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

问题描述

在一个操场上一排地摆放着N堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。请设计一个程序，计算出将N堆石子合并成一堆的最小得分和最大得分。

问题分析

我们对n的取值逐步分析

当n=1时，没有进行合并，得分为0

当n=2时，只有一种合并的方案，得分为两堆石子之和

当n=3时，有两种得分方案，先合并左边两个，先合并右边两个，这两种方案的区别我们可以看成是起点不同，最后一次合并的得分都是这三堆石子的总数

当n=4时，有三种得分方式，分别是先合并后面三个，先合并后面两个，先合并后面一个（也就是先合并前面三个），这三种方案对应的起点是1、2、3，最后一次合并的得分都是这四堆石子的总数。

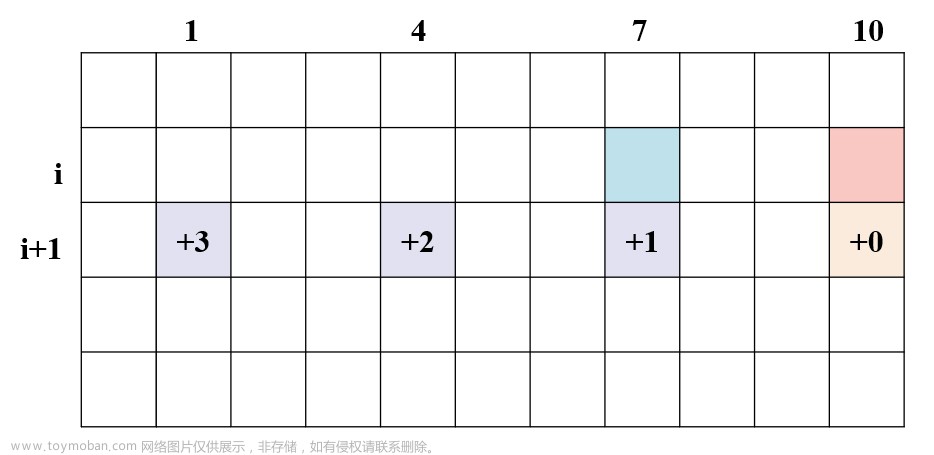
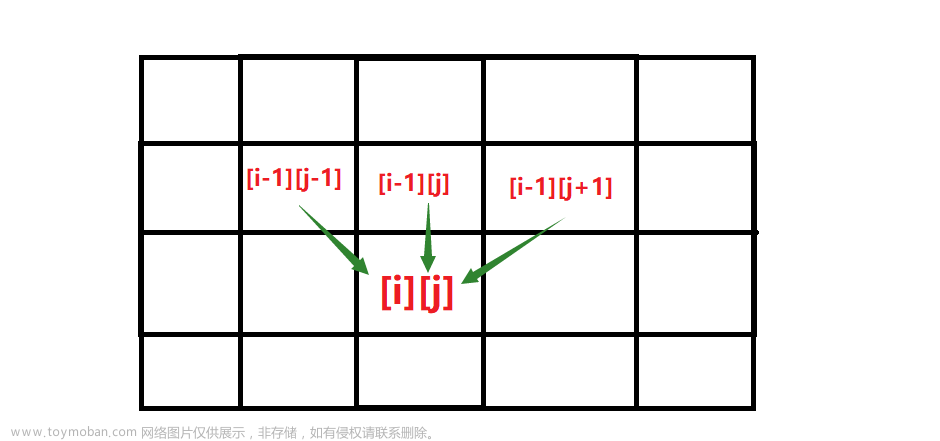
由此可知，我们所求的最大或者最小的得分就是这几种方案中得分最大或者最小的分数加上最n堆石子的总石子数，可得dp方程为：

存在k属于区间[i,j]

最大得分：dp[i][j] = max(dp[i][k] +dp[k+1][j]) + sum[i][j]

最小得分：dp[i][j] = min(dp[i][k] +dp[k+1][j]) + sum[i][j]

举例：

石子合并问题动态规划,动态规划,算法

代码实现：文章来源地址https://www.toymoban.com/news/detail-861254.html

#include <iostream>
#include <math.h>
using namespace std;

void fun(int c[],int n){
	//计算sum[][]
	int sum[100][100] = {0};
	for(int i = 0;i<n;i++){
		for(int j = 0;j<n;j++){
			if(i == j){
				sum[i][j] = c[j];
			}else if(j>i){
				sum[i][j] = c[j] + sum[i][j-1];
			}
		}
	}
	//准备两个二维数组分别用于求最大得分和最小得分 
	int dp1[100][100] = {0};
	int dp2[100][100] = {0};
	for(int len = 2;len<=n;len++){ //枚举区间 
		for(int i = 0;i < n-len+1;i++){	//枚举此区间的每一个起点,最大的起点是整排石子的长度从后面往前面减当前长度加一 
			//定义终点
			int j = i + len -1;
			dp1[i][j] = 1e8;
			dp2[i][j] = -1;
			for(int k = i;k<j;k++){	//从起点到终点一直遍历k，寻找最大最小得分· 
				dp1[i][j] = min(dp1[i][j],dp1[i][k] + dp1[k+1][j] + sum[i][j]);
				dp2[i][j] = max(dp2[i][j],dp2[i][k] + dp2[k+1][j] + sum[i][j]);
			} 
		}
	} 
	cout<<dp1[0][n-1]<<endl;
	cout<<dp2[0][n-1]<<endl;
}

int main(){
	int n;
	cin>>n;
	int c[100];
	for(int i = 0;i<n;i++){
		cin>>c[i];
	}
	fun(c,n);
	return 0;	
}

到了这里，关于【动态规划】之石子合并问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！