学习目的
SPSS第十九讲:秩相关分析怎么做?
软件版本
IBM SPSS Statistics 26。
原始文档
《小白爱上SPSS》课程
#统计原理
秩相关分析
前面我们学习过线性相关分析,已知线性相关分析针对的是符合正态性分布的连续型变量,然而在科学研究中,有些数据不符合正态性分布,有些数据也并不连续,只能用定序尺度来度量,这些数据该如何处理呢?此时,就要运用到秩相关分析了。让我们一起来学习如何运用秩相关分析吧。
秩相关分析,又称等级相关分析,是将两样本值按数据的大小顺序排列位次,以每个个体的位次代替实际数据而求得的一种统计量。它是反映等级相关程度的统计分析指标,常用的等级相关分析方法有Spearman相关分析和Kendall秩相关分析等。
其计算公式如下,若不太理解此公式,只要感受下公式之美,然后飘过…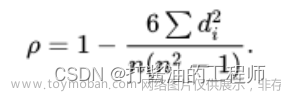
d代表X,Y的秩差。
一、实战案例
小白记录了篮球比赛前10名的名次和平均投篮命中率,见下表。试问名次与投篮命中率有无关系?
读数据:
GET
FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第十九讲 秩相关.sav'.

二、统计策略
针对上述案例,扪心七问。
Q1:本案例研究目的是什么?
A:关联分析。
Q2:分析的组数是多少呢?
A:两组数据。
Q3:本案例属于什么研究设计?
A:调查研究
Q4:有几个变量?
A:有两个变量。名次和平均投篮命中率。
Q5:变量类型是什么?
A:名次属于等级资料,命中率是连续性变量。
Q6:组内两变量数据服从正态分布么?
A:由于该项研究其中一个变量为等级资料,故无需检验另一连续变量的正态性,直接采用秩相关分析。
Q7:组内双变量关系是否为线性关系?
A:需要检验。
概括而言,如果数据满足以下条件,则采用秩相关分析。
三、SPSS操作
Step1:操作方式:“分析——相关——双变量——”;
Step2:由于有一个变量为等级变量,故选择Spearman;
命令行:
NONPAR CORR
/VARIABLES=名次 命中率
/PRINT=SPEARMAN TWOTAIL NOSIG
/MISSING=PAIRWISE.
四、结果解读

Spearman相关分析结果显示,r=-0.818, P=0.004, 具有统计学意义,不支持原假设(变量之间不存在相关性),表明篮球排名名次与命中率之间存在相关关系。
秩相关分析也可以选择Kendall相关分析。
命令行:
NONPAR CORR
/VARIABLES=名次 命中率
/PRINT=KENDALL TWOTAIL NOSIG
/MISSING=PAIRWISE.
结果如下:
Kendall相关分析表示,r=0.644, P=0.009,具有统计学意义,表明篮球排名名次与命中率之间存有相关。
五、规范表达
规范报告有多种方式,本公众号只提供一种方式供参考。
1、规范图表
(1)本例只有两个变量之间相关,建议采用散点图呈现结果更直观。
命令行:
GRAPH
/SCATTERPLOT(BIVAR)=名次 WITH 命中率
/MISSING=LISTWISE.

通过图表构建器添加线性拟合线:
* 图表构建器.
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=名次 命中率 MISSING=LISTWISE REPORTMISSING=NO
/GRAPHSPEC SOURCE=INLINE
/FITLINE TOTAL=YES.
BEGIN GPL
SOURCE: s=userSource(id("graphdataset"))
DATA: 名次=col(source(s), name("名次"))
DATA: 命中率=col(source(s), name("命中率"))
GUIDE: axis(dim(1), label("名次"))
GUIDE: axis(dim(2), label("命中率"))
GUIDE: text.title(label("包含拟合线的简单散点图 / 命中率 按 名次"))
ELEMENT: point(position(名次*命中率))
END GPL.

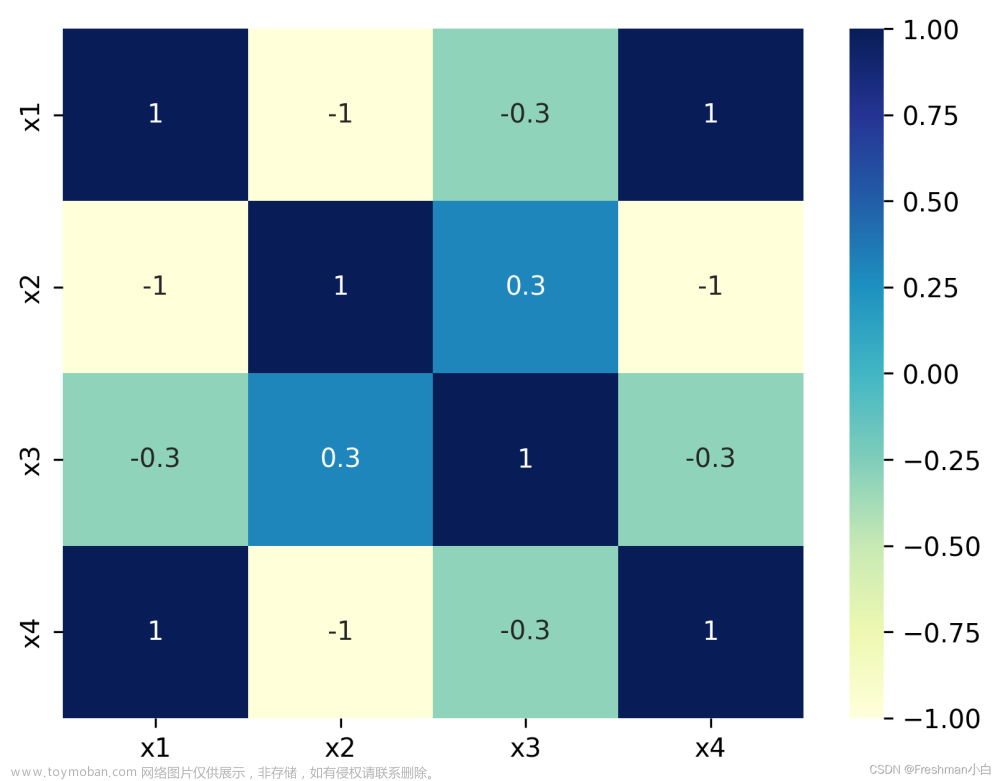
(2)若有多个变量之间两两相关,则采用相关矩阵表呈现(详见上一讲的相关矩阵表)
命令行(默认采用皮尔逊方法计算相关系数):
CORRELATIONS
/VARIABLES=名次 命中率
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE.

命令行(SPEARMAN方法计算相关系数):
NONPAR CORR
/VARIABLES=名次 命中率
/PRINT=SPEARMAN TWOTAIL NOSIG
/MISSING=PAIRWISE.

2、规范文字
Spearman相关分析结果显示,r=-0.818, P=0.004,具有统计学意义,表明篮球排名名次与命中率之间存在相关关系。文章来源:https://www.toymoban.com/news/detail-861479.html
六、划重点:
1.秩相关分析,又称等级相关分析,是将两样本值按数据的大小顺序排列位次,用每个样本的个体的位次代替实际数据而求得的一种统计量
2.秩相关分析主要针对两种情况:双变量至少有一个非正态分布的定量资料、至少一个变量为等级资料。
3.常用的等级相关分析方法有Spearman相关分析和Kendall秩相关分析等,通常采用Spearman相关。
4.不服从正态分布的定量资料可选择秩相关。定量资料采用Spearman分析会损失信息,降低检验效能,减少阳性的可能。文章来源地址https://www.toymoban.com/news/detail-861479.html
到了这里,关于学习笔记|秩相关分析|Spearman相关分析|Kendall相关分析|规范表达|《小白爱上SPSS》课程:SPSS第十九讲:秩相关分析怎么做?的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!