如何实现3D物品自动摆放,构建一个宜居的家居空间,这篇文章将告诉你答案!文末给出相关资料~
一、生成步骤
分两步生成给定房间的家具布置:
第一步:根据美学和功能规则,优化房间中家具对象的选择和布置。此过程通过【贪婪成本最小化算法】快速探索家具布局的无限跨维空间
根据室内设计规则形成的成本函数优化全局家具布局和对象选择。在此优化过程中,家具布置会因特定动作而随机改变,并且只有当新配置的成本低于原始室内设计的成本时,才接受新配置。
第二步:【程序方法】以随机方式局部应用以生成重要的场景细节
最终的设计通过较小的物体进行局部增强,以生成重要的场景细节。为此,我们使用一套程序,每个程序都针对特定的局部布置,例如桌子上的盘子、开口处的窗户等。
最后,通过材料优化实现统一的设计和和谐的色彩分布。
二、室内布局自动化
自动室内设计方法结合了优化和程序方法,为给定的虚拟房间生成宜居的室内设计。首先,大型家具对象的最优布局是通过贪婪成本优化算法生成的。在第二步中,使用程序方法来局部布置小物体(即房间装饰)。
贪婪成本优化和程序装饰的好处是我们的方法实现了全自动室内设计的交互速度。
1.空间组件布置优化
此过程使用贪婪成本最小化算法,在优化过程中用数据库中的家具对象填充虚拟房间。此优化的主要目标是为给定房间找到成本函数最小的家具布置。
成本函数的最小化工作原理如下:
-
首先,使用给定房间的适当对象随机生成家具布局。
-
然后,计算该布局的成本函数。
-
接下来,家具布局将通过一组移动(突变)进行更改。
-
最后,如果新配置的成本低于之前的配置,则可以接受。
-
通过迭代执行对成本函数的评估和新设计的生成,以达到最佳的家具布局。
1.1 类别组件属性定义
为了更好的应用算法执行如上过程,我们对家具定义成对象或组件,算法需要有关用于自动布局的组件的属性和关系的信息。为了简化向系统中添加新组件的过程,我们使用组件类别的概念并按类别存储所需的属性。然后,每个组件只需要表明它属于哪个类别,这些类别对应于组件的类型,例如“衣柜”或“桌子”。
来自一类的所有组件共享用于计算成本函数的相同属性。这些属性对应于专业设计实践中使用的测量和关系。我们的方法中针对每个类别的组件使用以下属性:
| 组件 |
属性类型 |
属性 |
说明 |
建议参数 |
举例 |
| 类型 |
常量 |
间隙约束 |
前、后、左、右。间隙约束指定组件周围的舒适使用所需的空白空间。 |
||
| 靠墙站立的概率 |
指定了一个物体站在墙附近的重要性 |
[0,1] |
|||
| 可能的父母 |
包含组件类别列表,这些组件类别可能是当前组件的父对组件。此外,使用到父组件的最小和最大距离,并指定朝向父组件的方向(正面或侧面)。 |
objlist |
|||
| 有父母的概率 |
表示组件与其他组件处于组关系中的重要性 |
[0,1] |
|||
| 房间重要性 |
说明组件对于特定空间的重要性。 |
[0,1] |
卧室中必须有一张床,因此该房间的重要性为 1.0。 |
||
| 所需计数 |
每个类别都包含特定空间中该类别的最小要求和最大允许数量 |
spacetype - [min, max] |
起居室最多可以放置一台电视机。 |
||
| 变量 |
位置 |
空间坐标 |
|||
| 形状 |
可以是3D包围盒 |
||||
| 朝向 |
地平面中的 2D 矢量 |
1.2 空间属性定义(特殊组件)
| 空间 |
属性 |
说明 |
建议参数 |
举例 |
| 类型 |
位置 |
世界坐标 |
||
| 形状 |
TODO:具体表示方式,调研中 |
1.3 组件布局调整策略
1. 随机改变组件的位置。
2. 随机改变组件的方向。
3. 将组件对象与最近的组件对齐。
4. 将组件与最近的墙壁对齐。
5. 将组件捕捉到最近的组件。
6. 将组件固定到最近的墙壁上。
7. 将组件与可能的父组件之一连接。
8. 向父组件添加新的子组件。
9. 将新组件添加到布局中。
10. 从布局中随机移除组件。
每一次迭代,如上策略的调整都以特定的概率下执行。在我们的实验中,使用以下经验值设置这些概率:
- 1至5:适用于每个组件,概率为0.3
-
6:对每个对象执行,概率为特定组件靠墙站立概率值
-
7:具有为特定属性组件定义有父对象及对应的概率值
-
8:父组件添加新子组件概率为0.6
-
9:添加组件到布局概率为0.5
-
10:从布局中随机删除的概率0.1
-
特别说明:动作8和9往布局中添加过程中,使用特殊启发式方法来实现子组件围绕父组件的对齐(例如:桌子周围的椅子)。此启发式将子组件定位到父中间件的相对侧,并根据其计数属性值对齐它们。且只接受不会导致组件相交的布局。
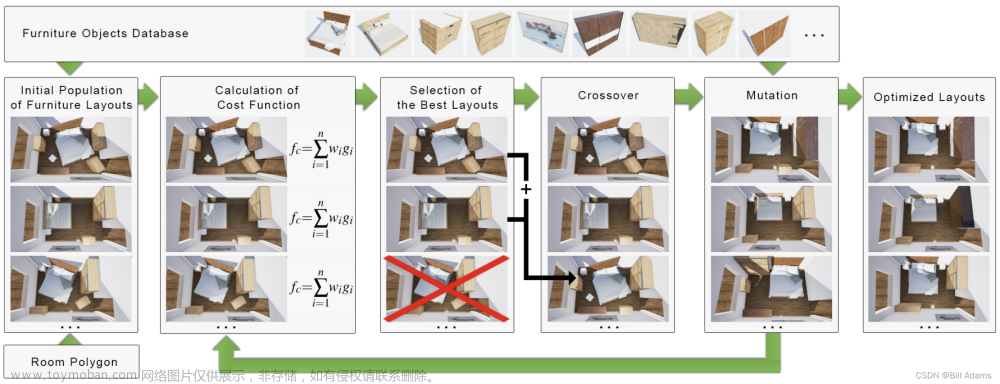
室内设计的成本计算均使用设计指南条款的加权和,该算法迭代地优化家具布局
基于遗传算法的处理策略:
选择(Selection):
我们的遗传算法优化通过从当前群体创建新一代家具布局来推进每次迭代。为了选择能够生存到下一代的设计个体,我们使用锦标赛选择。在比赛选择中,每个存活下来的个体都通过两个步骤来确定:首先,从岛上的子种群中随机选择 𝑘 个体。其次,从这些 𝑘 选出的个体中,成本值最低的个体是锦标赛的获胜者,并进入下一代。我们在实现中设置 𝑘 = 6。通过这种方法,我们的算法选择 70% 的群体进入下一代。剩下的 30% 是通过所选父母的交叉产生的。最后,我们对这个新创建的群体中的 50% 应用突变。
交叉(Crossover):
交叉是一种类似于自然界繁殖的计算操作,其中通过组合两个父母的基因组来创建新的后代。遗传算法使用交叉从选定父母的随机子部分创建新个体。在家具布局领域,个体是由家具对象的配置形成的。因此,通过从每个父布局中选择随机家具对象并将它们组合在一起形成新的家具布局,可以自然地进行交叉。在我们的方法中,30% 的新一代是由 70% 的选定个体交叉形成的。交叉操作的父母是随机选择的。通过将来自第一个父母的大约一半的家具物品与来自第二个父母的物品交换,形成一个新个体。如果第二个父对象的家具对象有子对象,这些子对象也会插入到新个体中。所选家具对象不会插入到新个体中,以防与现有对象发生交叉。
突变(Mutations):
在每次迭代结束时,我们的算法都会通过随机突变来改变 50% 的设计个体,以支持探索新的家具配置。我们的方法使用以下突变来改变个体:
(1)随机改变家具对象的位置。
(2)随机改变家具对象的方向。
(3) 将家具对象与最近的对象对齐。
(4) 将家具对象与最近的墙壁对齐。
(5) 将家具对象捕捉到最近的对象。
(6) 将家具对象固定到最近的墙壁上。
(7) 将家具对象与可能的父对象之一连接。
(8) 向父对象添加新的子对象。
(9) 将新的家具对象添加到设计个体中。
(10)从设计个体中移除随机对象。
详情见1.32.成本函数
算法根据成本函数优化组件布局,以达到给定空间最理想的组件布置,因此成本函数反映了专业设计师在实践中使用的规则。成本函数中使用以下规则及其数学表达式:
2.1 清除(Clearance)
功能组件需要在它们周围留出一个空白空间才能使用它们的主要功能。 有些组件需要从一侧或多侧直接访问。 间隙准则代表了这一要求。 我们将间隙准则建模为由间隙约束扩展的对象边界框之间的重叠量: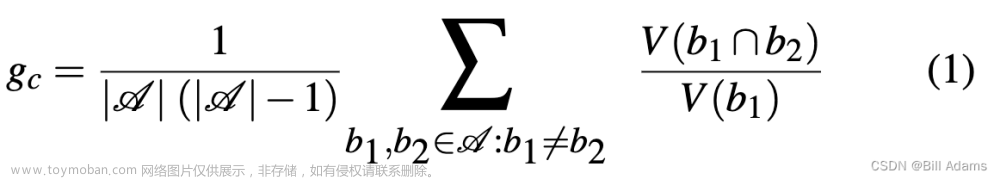
间隙表达式以成对的方式计算。b1和b2是集合𝒜的扩展边界框。集合𝒜包含一个组件布局中所有组件的扩展边界框,以及墙壁、窗户和门的边界框。函数V返回3D几何形状的体积,|𝒜|表示集合 的大小。
# 计算方法:
def calcLayoutClearance(self , objList, layoutPoly= None, entList = None):
"""
calculating layout polygons mean overlap
objList - List of obstacle objects (polygons)
Each object is assumed to represent the EXTENDED-bounding-box, i.e., including the extra gap
required around the object
layoutPoly - Nx2 list of ordered vertices defining a 2D polygon of N vertices - room polygon layout
last point NEQ first point
entList - List of entrance line segments (2D points). Entrances should not be occluded
"""
#
# =>>>>> CURRENTLY constraints are not included, e.g. entrance, window, power-outlet, TV
#
nObj = len(objList)
objListSp = []
# Transform to shapely
for n in range(nObj):
objListSp.append(sgp.Polygon([[p.x, p.y] for p in objList[n]]))
ovlpSum = 0
for m in range(nObj - 1):
for n in range(nObj):
if m == n:
continue
ovlp = objListSp[m].intersection(objListSp[n]).area
ovlpSum += ovlp / objListSp[m].area
ovlpSum = ovlpSum / (nObj * (nObj - 1))
# ==> entrance overlap
# if entLine.touches(tmpPolyLayout) or entLine.intersects(tmpPolyLayout):
# ovlp = entLine.intersection(tmpPolyLayout).length / entLine.length
return ovlpSum2.2 流通(Circulation)
流通指南表达了功能组件需要人类可以物理访问以发挥其功能的需求,即空间的任何部分都不应被阻塞以供人类居住和使用。我们通过无法从房间入口进入的物品数量来表达这一指导方针。为了计算这个数字,我们需要使用路径查找算法并评估从入口到家具对象的路径是否存在。
我们的方法使用回溯来寻找离散空间中的可能路径。这通过三个主要步骤完成:
-
第一步:所有功能组件和墙壁都投影到地平面并光栅化为 2D 网格
-
第二步:对这些投影应用扩张操作来解释身体大小,此操作通过指定人体半径的圆盘扩展离散投影
-
第三步:功能组件的正面在网格中被标记为从房间入口开始的路径可以访问的目标,然后开始回溯算法。
如上算法返回可访问目标的数量𝑛a,我们将当前布局中存在的功能组件总数标记为𝑛𝑡。流通准则的表达式可以写成:
我们对总体中的所有布局设置了一个硬约束,以包含至少2个功能组件。 因此对于所有定义的方程,𝑛𝑡>1成立,进而避免了除以零。
# 计算方法
def findPathPoly(self ,sourceP, targetP, objList, layoutPoly):
"""
calculating shortest path from sourceP point to targetP that avoid polygon shape obstacles
sourceP/targetP - 2D points
objList - List of obstacle objects (polygons, each is a list of 2D points).
Should Contains the object's polygon and forward facing edge ???
layoutPoly - Nx2 list of ordered vertices defining a 2D polygon of N vertices - room polygon layout
last point NEQ first point
=>>>>>>> Assuming polygons DO NOT intersect
"""
nObj = len(objList)
objListVg = []
# Transform to pyvisgraph format
for n in range(nObj):
tmpPoly = []
for p in objList[n]:
tmpPoly.append(pvg.Point(p.x,p.y))
objListVg.append(tmpPoly)
# Start building the visibility graph
graph = pvg.VisGraph()
refPoint = pvg.Point(sourceP[0].x, sourceP[0].y)
workers = 1
graph.build_mod(objListVg, workers, None, refPoint) # , workers=workers)
# graph.build(objListVg) #, workers=workers)
# Get the shortest path
shortest_path = []
path_distance = []
direct_distance = []
for n in range(len(sourceP)):
sP = pvg.Point(sourceP[n].x, sourceP[n].y)
tP = pvg.Point(targetP[n].x, targetP[n].y)
spath = graph.shortest_path(sP, tP)
# Calculate the total distance of the shortest path
pdistance = 0
prev_point = spath[0]
for point in spath[1:]:
pdistance += np.sqrt((prev_point.y - point.y) ** 2 + (prev_point.x - point.x) ** 2)
prev_point = point
shortest_path.append(spath)
path_distance.append(pdistance)
dDist = np.sqrt((targetP[n].x - sourceP[n].x) ** 2 + (targetP[n].y - sourceP[n].y) ** 2)
direct_distance.append(dDist)
# print('Shortest path distance: {}'.format(path_distance))
return shortest_path, path_distance, direct_distance
def calcLayoutCirculation(self ,objList, srcList, tgtList):
"""
calculating layout polygons accessibility from entrance (could be more than one entrance)
objList - List of obstacle objects (polygons)
Each object is assumed to represent the EXTENDED-bounding-box, i.e., including the
extra gap
required around the object
src/tgt-List - pairs of points between which shortest path is calculated and compared to straight
path
"""
# print(objList)
# print(srcList)
nPairs = len(srcList)
pathRatioSum = 0
sPath, lenPath, dirPath = self.findPathPoly(srcList, tgtList, objList, [])
for n in range(nPairs):
pathRatioSum += (1 - dirPath[n] / lenPath[n])
return pathRatioSum2.3 组关系(Group Relationships)
室内设计中的功能组件可以根据其功能和类型进行分组。通常一组组件都有其父组件(例如:椅子位于桌子周围), 组内空间组织符合特定要求, 这些要求之一是人们的舒适交谈。而舒适的谈话取决于座位的位置,座位应支持眼神交流和正常的语音音量(即有限的距离), 我们用同类组件的平均距离来表示组关系成本: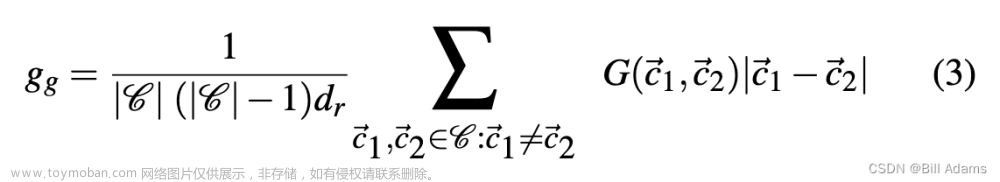
其中𝑑r是房间在地平面中的对角线尺寸。𝒞是房间中所有功能组件中心的集合。如果中心𝑐1, ⃗𝑐2属于同一类别的对象函数𝐺(⃗𝑐1, ⃗𝑐2)返回 1,否则返回 0。
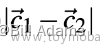
表示向量的大小。
# 计算方法
def calcGroupRelation(self ,objPos, membershipVec, dR):
"""
calculating object inter-group-relations: spread of objects from a group relative to space diagonal
objPos - vector of objects' center (numpy array)
membershipVec - vector of objects' membership association (integers)
dR - space diagonal (scalar)
"""
gSum = 0
nObj = len(objPos)
for i in range(nObj - 1):
for j in range(i + 1, nObj):
p = np.array(objPos[i]) - np.array(objPos[j])
p1 = np.array([p.x,p.y])
gSum += 1.0 * (not (membershipVec[i] - membershipVec[j])) * npla.norm(p1)
gSum /= ((nObj - 1) * nObj / 2 * dR)
return gSum2.4 对齐(Alignment)
在室内设计中,组件应正确定向并与其支撑表面对齐(例如:橱柜的背面应朝向墙壁)。此外功能组件应与其他对组件对齐。我们通过组件前向量之间角度的变化以及组件与其最近墙壁之间的概率距离测量来模拟对齐指南。对齐项以成对的方式评估: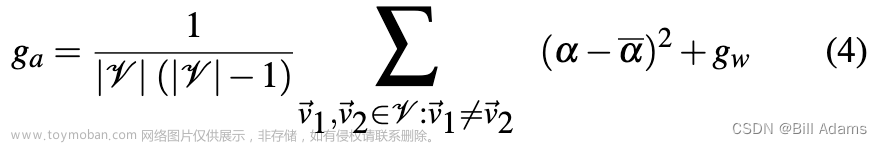

a与两个前向量𝑣1和𝑣2之间的角度成正比。𝒱是所有功能组件的前向量集合。我们还将房间墙壁的前向量包含在𝒱中以允许功能组件与墙壁对齐。 a-是a中所有向量的平均值。 等式5将𝑣1和𝑣2之间的角度的余弦从范围 (-1,1)重新映射到 (0,1) 以用作成本函数的一项。
除了适当对齐功能组件外,其中一些还应靠墙站立, 因此我们将墙距离项𝑔w添加到对齐成本中。 该术语使用为每个组件类别定义的靠墙pw的概率
~pb 是功能组件背面的点。 集合𝒫 表示来自当前室内设计中存在的所有功能组件的这些后点的集合。 函数projw(~pb)将点~pb投影到其最近的墙壁并返回此投影点。dr是房间在地平面中的对角线尺寸,如果房间不是矩形,那么dr被计算为房间边界框的对角线大小。
# 计算方法
def calcAlignment(self,backPos, walls, wallProbVec, dR):
"""
calculating object alignment, currently only w.r.t. supporting wall
backPos - vector of objects' back position (numpy array)
walls - list of walls, each represented as a line (end points)
wallProbVec - probability vector of objects' to stand against the wall
dR - space diagonal (scalar)
"""
#
# ====> DIDNOT check direction, i.e. that object is parallel/perpendicular to wall
#
nW = len(walls)
nO = len(backPos)
wLines = []
for iW in range(nW):
wLines.append(sgls.LineString((walls[iW][0], walls[iW][1])))
wSum = 0
for iO in range(nO):
dP = np.array([])
for iW in range(nW):
# shortest distance to wall
dP = np.append(dP, wLines[iW].distance(spt.Point(backPos[iO])))
wSum += wallProbVec[iO] * min(dP)
wSum /= (nO * dR)
return wSum
def Aligment_transformation(self , objects_list , dR_room):
all_objects_front_center_points = []
all_objects_back_center_points = []
for item in objects_list:
x1 =int(item["point"].x)
y1 = int(item["point"].y)
x2 = x1 + int(item["furniture"].top_right.x)
y2 = y1 + int(item["furniture"].top_right.y)
if (self.rotation == 0):
front = self.midpoint(Point(x1,y1),Point(x2,y1))
back = self.midpoint(Point(x1,y2),Point(x2,y2))
elif (self.rotation == 1):
front = self.midpoint(Point(x1,y2),Point(x1,y1))
back = self.midpoint(Point(x2,y2),Point(x2,y1))
elif (self.rotation == 2):
front = self.midpoint(Point(x2,y2),Point(x1,y2))
back = self.midpoint(Point(x2,y1),Point(x1,y1))
elif (self.rotation == 3):
front = self.midpoint(Point(x2,y1),Point(x2,y2))
back = self.midpoint(Point(x1,y1),Point(x1,y2))
all_objects_front_center_points.append(front)
all_objects_back_center_points.append(back)
# all_objects_front_points.append(front)
walls = []
walls.append(((0, 0), (100, 0)))
walls.append(((100, 0), (100, 100)))
walls.append(((100, 100), (0, 100)))
walls.append(((0, 100), (0, 0)))
wallProbVec = np.array([0.2, 0.2, 0.4, 0.6,0.2,0.6])
# dR = 600
return (self.calcAlignment(all_objects_back_center_points,walls,wallProbVec,dR_room))2.5 分布和节奏(Distribution and Rhythm)
根据该准则,功能组件应在空间中适当分布,并且这种分布的频率应遵循一定的节奏(例如:画作应该沿着墙上的一条线分布,它们之间的距离有节奏地重复)。 我们将此准则的成本建模为组件对之间的相对距离的方差: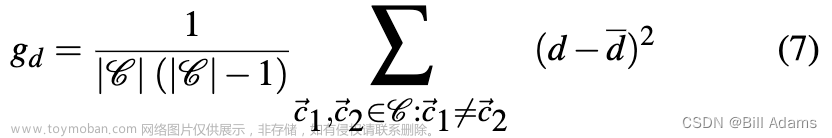

𝑑 代表两点之间的相对距离,𝑑m即欧几里得距离除以场景中两个组件之间的最大距离 。~d是室内设计中所有组件对之间的平均相对距离。
def calcObjDistrib(self ,objPos):
"""
calculating object distribution in space, also referred to as Rhythm
"""
nObj = len(objPos)
# get all pairs distance
dP = np.array([])
for i in range(nObj - 1):
for j in range(i + 1, nObj):
p = np.array(objPos[i]) - np.array(objPos[j])
dP = np.append(dP, npla.norm(np.array([p.x, p.y])))
dMx = np.max(dP)
dP /= dMx
dPmean = np.median(dP)
dSum = 0
for n in range(len(dP)):
dSum += (dP[n] - dPmean) ** 2
dSum /= len(dP) # ((nObj-1)*nObj/2)
# ==>>>> Maybe calculate sqrt(dSum), i.e. the Sigma and not Variance
return dSum2.6 视图平截头体(Viewing Frustum)
在优化的布局中,一些组件的主要功能应该从其他组件可见(例如:电视应该从沙发上可见)。 在我们的方法中,这些组件符合父子关系。 因此我们通过在所有父子对之间投射光线来计算视锥体成本,并计算与其他功能组件相交的光线数量。 我们将相交光线的数量表示为 𝑛𝑖 ,将室内设计中的物体总数表示为 𝑛𝑡。 视锥体成本可以计算为:
2.7 功能需求(Functional Needs)
空间中的功能组件用于该空间的特定功能或活动。 因此一个特定的空间应该包含对这个空间的活动很重要的内部物品(例如:客厅应该包含电视和沙发)。 我们对功能需求的表达由两个术语组成:
等式10中的第一项与当前设计个体中存在的所有功能组件的空间重要性有关。该术语将更高的成本分配给对当前空间不太重要的组件。重要性成本总结了设计个体中存在的组件的重要性值 io。I 是这些重要性值的集合。第二项与房间中特定类别的对象的期望数量有关。函数∆(𝑜𝑐) 计算类别 𝑜𝑐 的对象数与该类别的所需对象数之间的差异。集合 𝑂 代表当前室内设计中存在的所有类别。
# 计算方法
def calcFunctionality(self,impVec, objCatNum, catDesNum):
"""
calculating objects functionality importance and quantity
impVec - vector of importance values
objCatNum - amount of objects from each category in the layout (dict)
catDesNum - desired amount of objects from each category (dict)
#CALLING
actual_amounts = {'Table':2,'Chair':2,'Bed':2}
desired_amounts = {'Table':1,'Chair':4,'Bed':1}
r1.calcFunctionality(r1.object_importance,actual_amounts,desired_amounts)
"""
nO = len(impVec)
fSum1 = np.sum(1-impVec)
fSum1 /= nO
fSum2 = 0
for oc in objCatNum.keys():
fSum2 += abs(objCatNum[oc] - catDesNum[oc])
fSum2 /= (1.0 * len(objCatNum))
fSum = 0.5 * (fSum1 + fSum2)
return fSum2.8 占比(Proportion)
功能组件应与特定空间以及彼此之间具有适当的比例。此外如果空间内有太多空置空间,则应生成新组件。我们将此准则的成本建模为组件覆盖的体积与空间体积的比率:
Vo 是所有功能组件的总体积,Vr 是空间的总体积。 将这两个体积与组件覆盖的体积所需的比例rv进行比较。我们在实验中rv使用了0.45 值。 我们凭经验发现这些值最适合我们的优化。 体积Vr 还取决于空间的高度。 因此,较高的空间最好根据比例准则选择较高的功能组件。
# 计算方法
def calcProportion(self ,objList, roomPoints, desRatio = 0.45):
"""
Till now on the basis of area not volume
calculating layout-volume-to-room-ratio
objList: List of all points of each object in room
roomVol: Room points
"""
nObj = len(objList)
objListSp = []
# Transform to shapely
for n in range(nObj):
objListSp.append(sgp.Polygon([[p.x, p.y] for p in objList[n]]))
roomSp = sgp.Polygon([p.x, p.y] for p in roomPoints)
objVolSum = 0
for i in range(len(objListSp)):
objVolSum += objListSp[i].area
roomVol = roomSp.area
gP = max(desRatio - 1.0 * objVolSum / roomVol, 0) / (1.0 * desRatio)
return gP2.9 黄金分割(Golden Section)
该术语基于艺术和设计中常用的黄金分割原理,这一原则建议对空间进行令人赏心悦目的细分。我们将空间矩形从每一侧以黄金分割比例的线进行细分,分割率近似为 0.618。这四个细分线在设计中用作主要组件的位置。因此,我们根据功能组件与其最近的黄金分割线的距离来评估黄金分割成本:
~c 代表功能组件和项目的中心,projgs(~c)返回该中心到最近的黄金分割线的投影。
# 计算方法
def calcGoldenSec(self,objPos, roomRect, dR):
"""
calculating objects location w.r.t. golden section lines
objPos: objects' center position
roomRect: 4 points of room (or sub-area) rectangle
dR: room diagonal
"""
# make sure the vertices are ordered
tmpRect = sgp.Polygon([p.x, p.y] for p in roomRect)
tmpRect = tmpRect.convex_hull
t_rect = tmpRect.exterior.coords[0:-1]
# creating golden lines. Assuming gsRatio = 13/21
# go over the 2 consecutive pair of vertices and generate the 4-lines, 2 in each side
gsr = 13.0 / 21.0
line1 = sgls.LineString((t_rect[0], t_rect[1]))
length = npla.norm(np.array(t_rect[0]) - np.array(t_rect[1]))
pt11 = line1.interpolate(length * (1.0 - gsr))
pt12 = line1.interpolate(length * gsr)
line3 = sgls.LineString((t_rect[2], t_rect[3]))
length = npla.norm(np.array(t_rect[2]) - np.array(t_rect[3]))
pt32 = line3.interpolate(length * (1.0 - gsr))
pt31 = line3.interpolate(length * gsr)
line2 = sgls.LineString((t_rect[1], t_rect[2]))
length = npla.norm(np.array(t_rect[1]) - np.array(t_rect[2]))
pt21 = line2.interpolate(length * (1.0 - gsr))
pt22 = line2.interpolate(length * gsr)
line4 = sgls.LineString((t_rect[3], t_rect[0]))
length = npla.norm(np.array(t_rect[3]) - np.array(t_rect[0]))
pt42 = line4.interpolate(length * (1.0 - gsr))
pt41 = line4.interpolate(length * gsr)
gsLines = []
gsLines.append(sgls.LineString((pt11, pt31)))
gsLines.append(sgls.LineString((pt12, pt32)))
gsLines.append(sgls.LineString((pt21, pt41)))
gsLines.append(sgls.LineString((pt22, pt42)))
dObjGs = []
for i in range(len(objPos)):
dd = []
for j in range(len(gsLines)):
dd.append(gsLines[j].distance(spt.Point(objPos[i])))
dObjGs.append(min(dd))
gP = np.sum(dObjGs)
gP /= (1.0 * dR * len(objPos))
return gP文章来源地址https://www.toymoban.com/news/detail-861506.html
2.10 成本函数(Cost Function)
空间布局优化的成本函数定义为上述定义项的加权和:
每个指南的权重是在我们的实验中根据经验设定的,对大多数权重使用值1.0,流通(Circulation)权重设为1.1,占比(Proportion)权重设为2.5。增加了占比权重是因为此规则对于将组件插入场景至关重要。另外我们把功能需求(Functional Needs)权重设置到 3.0,因为这条规则对于向特定空间添加合适的组件非常重要。最后将黄金分割(Golden Section)权重设置为0.5。我们发现这些权重最适合我们的系统,并且我们在所有实验中都使用了它们。
# 计算方法
def Aligment_transformation(self , objects_list , dR_room):
all_objects_front_center_points = []
all_objects_back_center_points = []
for item in objects_list:
x1 =int(item["point"].x)
y1 = int(item["point"].y)
x2 = x1 + int(item["furniture"].top_right.x)
y2 = y1 + int(item["furniture"].top_right.y)
if (self.rotation == 0):
front = self.midpoint(Point(x1,y1),Point(x2,y1))
back = self.midpoint(Point(x1,y2),Point(x2,y2))
elif (self.rotation == 1):
front = self.midpoint(Point(x1,y2),Point(x1,y1))
back = self.midpoint(Point(x2,y2),Point(x2,y1))
elif (self.rotation == 2):
front = self.midpoint(Point(x2,y2),Point(x1,y2))
back = self.midpoint(Point(x2,y1),Point(x1,y1))
elif (self.rotation == 3):
front = self.midpoint(Point(x2,y1),Point(x2,y2))
back = self.midpoint(Point(x1,y1),Point(x1,y2))
all_objects_front_center_points.append(front)
all_objects_back_center_points.append(back)
# all_objects_front_points.append(front)
walls = []
walls.append(((0, 0), (100, 0)))
walls.append(((100, 0), (100, 100)))
walls.append(((100, 100), (0, 100)))
walls.append(((0, 100), (0, 0)))
wallProbVec = np.array([0.2, 0.2, 0.4, 0.6,0.2,0.6])
# dR = 600
return (self.calcAlignment(all_objects_back_center_points,walls,wallProbVec,dR_room))
def group_relationship_transformation(self ,objects_list ,roomPoints , dR_room):
"""
Transformation function for group_relationship and rythm and GoldenSec
"""
all_items_center = []
furniture_type = []
for idx,item in enumerate(objects_list):
centr_point = baseParent.center(self , idx)
all_items_center.append(geometry.Point(centr_point.x,centr_point.y))
furniture_type.append(item["furniture"].room_type)
# roomPoints= [geometry.Point(0,0),geometry.Point(100,0)
# ,geometry.Point(100,100),geometry.Point(0,100)]
# dR_room = np.sqrt(100**2+100**2) #Diagonal Size of the room
group_Relation = self.calcGroupRelation(all_items_center,furniture_type,dR_room)
objectDistribution = self.calcObjDistrib(all_items_center)
goldenSection = self.calcGoldenSec(all_items_center,roomPoints,dR_room)*0.5
return(group_Relation + objectDistribution + goldenSection)
def circulation_transformation (self ,objects_list):
"""
Transforms
"""
all_objects_points = []
sp_list = []
tp_list = []
for item in objects_list:
current_object_points = []
x1 =int(item["point"].x)
y1 = int(item["point"].y)
x2 = x1 + int(item["furniture"].top_right.x)
y2 = y1 + int(item["furniture"].top_right.y)
p1 = geometry.Point(x1,y1)
p2 = geometry.Point(x2,y1)
p3 = geometry.Point(x2,y2)
p4 = geometry.Point(x1,y2)
sp = geometry.Point(0,0)
tp = p1
current_object_points = [p1,p2,p3,p4]
all_objects_points.append(current_object_points)
sp_list.append(sp)
tp_list.append(tp)
cost = self.calcLayoutCirculation(all_objects_points,sp_list,tp_list)*1.1
return(cost)
def clearnace_transformation (self , objects_list,roomPoints):
"""
Transformation function for clearance and proportion
"""
all_objects_points = []
for item in objects_list:
current_object_points = []
x1 =int(item["point"].x)
y1 = int(item["point"].y)
x2 = x1 + int(item["furniture"].top_right.x)
y2 = y1 + int(item["furniture"].top_right.y)
p1 = geometry.Point(x1,y1)
p2 = geometry.Point(x2,y1)
p3 = geometry.Point(x2,y2)
p4 = geometry.Point(x1,y2)
current_object_points = [p1,p2,p3,p4]
all_objects_points.append(current_object_points)
clearance = self.calcLayoutClearance(all_objects_points)
# roomPoints= [geometry.Point(0,0),geometry.Point(100,0)
# ,geometry.Point(100,100),geometry.Point(0,100)]
proportion = self.calcProportion(all_objects_points,roomPoints)*2.5
return (clearance + proportion)
def cost_function(self , objects_list ,roomPoints ,dR_room):
clearance_proportion=self.clearnace_transformation(objects_list,roomPoints)
circulation = self.circulation_transformation(objects_list)
groupRelationship_rythm_goldSec = self.group_relationship_transformation(objects_list,roomPoints,
dR_room )
alignment = self.Aligment_transformation(objects_list , dR_room)
actual_amounts = {'Table':2,'Chair':2,'Bed':2}
desired_amounts = {'Table':1,'Chair':4,'Bed':1}
Functionality = self.calcFunctionality(self.object_importance,actual_amounts
,desired_amounts)*3
result = clearance_proportion + circulation + groupRelationship_rythm_goldSec + Functionality + alignment
return(result)3.程序装饰
装饰元素和日常使用的小物品使室内空间感觉更加舒适和有人居住。因此我们通过使用小对象进行程序装饰来增强自动家具布局的方法。程序装饰局部调用将装饰物布置到房间的程序,由我们贪婪的成本最小化提供。这些过程通常根据给定的定位规则将物体定位到支撑表面上(例如办公桌上的笔记本电脑)。我们还允许在给定的空间和角度维度范围内随机放置对象。每个装饰过程都分配了一组对象,可以通过为此过程给出的规则来定位这些对象。在将对象放入场景之前,会评估与现有对象的碰撞,如果发生碰撞,则不会插入该对象。我们将以下程序集成到我们的系统中:
3.1 窗户装饰
通常房间的重建几何体包含窗户的开口,但这些开口中没有插入窗户模型。因此我们的程序从数据库中选择最适合窗户开口纵横比的窗户模型,以尽量减少窗户模型的变形。最后缩放窗户模型以适合开口并正确定位。
窗帘:经常用作室内空间的装饰元素。因此如果周围的墙壁和物体允许,我们的程序装饰会将窗帘放置在窗户前面。窗帘按比例缩放以适应房间的高度并围绕窗户空间。在实验中我们缩放了窗帘的宽度以覆盖窗户宽度的140%。
百叶窗:可用于控制室内空间的光量,因此通常是内部或外部的一部分。百叶窗定位程序首先选择数据库中最适合窗户开口的 3D 模型,然后对其进行缩放并定位在窗户前面。
3.2 门装饰
此过程将门对象定位到房间几何形状的门洞中,选择合适的门型号及其位置的过程与窗户的过程相同,不同之处在于它使用不同的一组 3D 模型进行定位。
3.3 桌子装饰
室内空间的桌子有不同的用途,它们总是用作日常使用元素的支撑面,例如餐具、鲜花或办公设备。由于不同房间的桌子用途不同,我们的程序根据使用它们的房间来装饰桌子。我们实现了厨房、客厅和办公室的桌子装饰。每个房间都有其特定的一组对象来装饰桌子。餐桌装饰利用桌椅的亲子关系,增加盘子和餐具位于每把椅子前面的桌子上。对于办公室和客厅的桌子,物体随机定位,更有可能位于桌子的中央。办公桌上物体的旋转是以每个物体的前向量指向椅子的方式计算的。该方向随机扰动,允许的偏航角变化为 15 度。最后,如果桌子周围有足够的空间可以插入地毯,则厨房和客厅的桌子下面的地板可以用地毯装饰,地毯模型也是从数据库中随机选择的。
3.4 转角装饰
在室内设计中,空的角落可以用植物、灯具或其他物体来装饰。因此我们将角落装饰的程序集成到我们的系统中。算法首先找到由墙壁和家具形成的角点。然后,将来自特定 3D 模型集的随机装饰对象放置到这些角落,直到放置的装饰对象的数量达到所需数量。在我们的实验中使用经验设置的数字 3 作为角装饰对象的所需数量。
3.5 水平表面的装饰
有人居住的室内空间倾向于使用水平表面(例如架子或柜子的顶桌)来存放装饰物或日常用品(例如书籍、花瓶、蜡烛)。因此我们集成了将装饰物定位到空的水平表面上的程序。实施中我们使用橱柜和架子作为基础水平表面,装饰程序从数据库中随机选择一个装饰对象并将其放置在基面上的随机位置上,此放置使用对象的边界框来防止对象覆盖在基础表面的边缘上。
我们的程序装饰涵盖了放置小物件和装饰物的最常见空间。然而可以通过向系统中添加新程序来扩展程序装饰。每个新程序都应该使用自己的一组装饰对象以及自己的规则来相对于现有的家具配置来定位对象。我们在基于 C++ 的虚幻引擎 4 中实现了我们的算法。装饰程序是用C++语言实现的。没有和有程序装饰的带家具房间的比较如下图所示。

没有(左)和有(右)程序装饰的最终家具布置。从上到下显示的场景为:卧室、厨房、客厅、办公室
三、材料优化
通过引入表面类别并为属于特定类别的所有表面选择一种通用材料来实现材料的一致性。在实验中使用以下类别的表面:织物、木材、玻璃、铬、金属、塑料、陶瓷和石头。通过使用材料数据库将一种材料随机分配给每个表面类别。
此外使用来自导入几何模型的材料名称来识别特定类别的表面,即如果类别名称与此表面上的部分材料名称匹配,则该表面被分配给一个类别。此方法对具有相同类别的表面进行分组,然后通过针对数据驱动的成本函数优化每个类别的材料分配来实现房间内材料的颜色和谐。我们的成本函数模拟场景中存在的颜色之间的颜色兼容性,使用贪心算法来最小化这个成本函数。在每次优化迭代中执行以下步骤:
-
为每个类别随机选择一种材料并将其分配给该类别的表面
-
从与房间角落对齐的四个视点渲染场景
-
从渲染图像中提取 5 种主色
-
通过计算提取的 5 色调色板的成本来评估场景中的颜色兼容性
-
如果新分配的材料的成本函数低于之前分配的成本函数,则接受这个新的材料配置
颜色兼容性
材质的优化使用颜色兼容性来为场景中的每种材质配置分配成本。使用由 5 种颜色组成的调色板来表示场景中的主色。调色板中的颜色在 CIELab 颜色空间中表示,通过 k-means 聚类从场景的渲染图像中提取调色板。然后使用和谐调色板数据库来计算提取调色板的成本。带有提取调色板的室内设计场景如下图所示:

顶部:我们的系统优化的室内设计布局和材料。底部:提取的 5 调色板。
提取的调色板𝑓𝑝的成本是根据我们的和谐颜色数据库中k最近调色板的加权距离计算的:

𝑝𝑖 是与提取的调色板 𝑝𝑒 第 i 个最接近的调色板,𝑟𝑖 是调色板 𝑝𝑖 的评级。我们数据库中的评级已标准化。我们在实验中使用 𝑘 = 10。调色板的距离 |𝑝𝑖 − 𝑝𝑒|计算为 CIELab 颜色空间中调色板中各个颜色之间的距离之和:

其中 𝑝𝑖𝑐 和 𝑝𝑒𝑐 是相应调色板中的第 c 个颜色。距离 |𝑝𝑖𝑐 − 𝑝𝑒𝑐|是 CIELab 色彩空间中的欧几里德距离。所有调色板中的颜色按 L 值排序,以计算相应颜色之间的距离。
颜色兼容性数据库
我们的和谐色彩数据库包含 100000 个带有指定等级的调色板。该数据库是通过使用艺术家创建的和谐调色板形成的,这些调色板从在线资源 www.colourloves.com 获得。我们从 Colourloves 网站下载了 500000 个带有用户评分的调色板。这些调色板包含一般设计任务中使用的颜色,包括网页设计、建筑设计、室内设计等。我们使用基于图像的方法来选择适合室内设计的调色板。我们从互联网上下载了 10000 张室内设计图像,并通过 k 均值聚类提取了它们的主要调色板。然后,每个调色板的室内设计适宜性评级。Colourlovers 计算为从提取的室内设计调色板中到 k 最近调色板的平均距离。提取的调色板被添加到下载的调色板中,形成和谐色彩的初始数据库。该数据库中的每个调色板都被分配了一个新的评级𝑟𝑖,计算公式为𝑟𝑖 = 0.6𝑟𝑒 + 0.4𝑟𝑐,其中𝑟𝑒是从室内设计图像中提取的评级,𝑟𝑐是来自Colourlovers数据库的用户评级。两个评级首先通过最大值进行归一化。权重 0.6 和 0.4 是根据经验设置的。从图像中提取的调色板的用户评级 𝑟𝑐 为 1.0。
最后,我们通过选择 100000 个具有最佳评级𝑟𝑖的调色板形成了我们的和谐调色板数据库。该数据库用于我们的贪婪材质优化,以选择具有和谐颜色的材质配置。我们的材料优化前后的室内设计结果可以在补充文件中看到。此外,我们的系统不仅能够优化家具材料,还能够优化墙壁和地板的材料。
四、相关资料
1.基于遗传算法的室内自动布局
-
论文:https://publik.tuwien.ac.at/files/publik_262718.pdf
-
源码:见上传附件文章来源:https://www.toymoban.com/news/detail-861506.html
2.基于成本最小化贪婪算法室内自动布局
-
论文:http://www.peterkan.com/download/ieeevr2018.pdf
-
源码:见上传附件
到了这里,关于苦于实现3D空间自动布局的同学,请参考:3D室内空间布局自动化算法分析(含源码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!