数据结构——栈（C++实现）

今天我们来看一个新的数据结构——栈。

什么是栈

栈是一种基础且重要的数据结构，它在计算机科学和编程中扮演着核心角色。栈的名称源于现实生活中的概念，如一叠书或一摞盘子，新添加的物品总是放在顶部，而取出物品时也总是从顶部开始。这种后进先出（Last In, First Out, LIFO）的特性决定了栈的行为。

以下是栈的核心特征和操作：

1. 结构与访问限制：
栈是一个线性数据结构，其中元素按照一定的顺序排列。然而，不同于数组或链表，栈只允许在一端（通常称为栈顶）进行数据的插入（也称为压入，push）和删除（也称为弹出，pop）操作。另一端（栈底）是固定的，不参与数据的直接增删。这意味着栈的元素访问受到严格的限制，用户只能与栈顶元素进行交互。
2. 后进先出（LIFO）原则：
栈遵循后进先出原则。这意味着最近添加到栈中的元素最先被移除。换句话说，最后压入栈的元素是离栈顶最近的，因此在弹出操作时会第一个被访问和移除。相反，最早压入栈的元素（即那些距离栈顶最远的元素）只有在所有后来压入的元素都被弹出后才能被访问。
3. 基本操作：

• Push（压入）： 将一个元素添加到栈顶。
• Pop（弹出）： 移除并返回栈顶元素。如果栈为空，尝试弹出操作通常会导致错误或异常。
• Peek（查看）/Top： 返回栈顶元素的值，但不改变栈的状态（不移除元素）。
• IsEmpty（是否为空）/Size（大小）： 检查栈是否为空或获取栈中元素的数量。
  4. 应用场景：
  栈因其简单且高效的特性在许多编程任务中得到广泛应用，包括但不限于：
• 函数调用栈： 在编程语言实现中，每当一个函数被调用时，其局部变量、返回地址等信息会被压入一个系统维护的栈中。函数执行完毕后，通过弹出操作清除这些信息，返回到调用函数的位置继续执行。
• 表达式求值和符号解析： 在计算逆波兰表示法（RPN）表达式或处理编程语言的括号匹配时，栈用于临时存储操作数和运算符，确保正确的计算顺序。
• 深度优先搜索（DFS）和回溯算法： 在遍历树形结构或解决涉及多种可能路径的问题时，栈用于存储待访问节点或中间状态，以便回溯到前一个状态。
• 浏览器历史记录： 用户浏览网页时，后访问的页面压入历史记录栈，前进和后退操作对应于栈的弹出和压入。

总的来说，栈是一种高效、受限的线性数据结构，通过其特有的后进先出性质，为处理需要保持数据顺序、尤其是需要频繁撤销最近操作的场景提供了简洁而强大的工具。

通俗理解，栈的确可以看作是一种操作受限的线性表。线性表是一类数据结构，其中的元素按一定顺序排列，每个元素都有一个唯一的前驱和后继（除了首尾元素外）。栈继承了线性表的这一基本特征，即元素间的线性关系。但是，与常规线性表相比，栈对元素的插入和删除操作施加了严格限制：

操作限制：
常规线性表通常允许在任意位置插入和删除元素，而栈只允许在表的一端（栈顶）进行这两种操作。这意味着你不能随意地在栈的中间或底部插入或删除元素，只能对栈顶进行操作。
行为特点：
由于这种操作限制，栈体现出后进先出（LIFO）的特性。想象一下一个真实的堆栈，比如一叠书或者一叠盘子。当你把新的物品（书或盘子）放在堆栈顶部时，它们就成了最新的“后进”元素。当你需要取走一个物品时，你只能从最上面拿走，所以取出的是最晚放入的那个“先进”元素。这就是所谓的“后进先出”。这种特性使得栈非常适合处理那些需要按照“最后来，最先走”顺序处理数据的场景。
通俗比喻：
可以把栈比作一个只能从上面放东西和取东西的箱子。往箱子里放物品（压入）时，新物品总是在最上面；取出物品（弹出）时，也只能拿走最上面那个。这样，箱子里的物品就像排队一样，后放入的总是在前面，先放入的在后面，想要取走一个物品，必须先把所有后来放入的物品都拿出来。

总结来说，虽然栈具备线性表的基本结构特点，但它通过严格限制操作位置，使其成为一种具有特定行为（后进先出）的特殊线性表。这种操作上的约束赋予了栈独特的应用场景和价值。

栈的实现

我们可以用数组来模拟栈的行为：

template<class T>
class MyStack
{
public:
    MyStack() //无参构造
        :_capacity(10)
        ,_size(0)
    {
        //开辟空间
        _data = new T(_capacity); //开辟这么大的空间
    }
		
    MyStack(const size_t& capacity) //带参构造
        :_capacity(capacity)
        ,_size(0)
    {
        //开辟空间
        _data = new T(_capacity);
    }	


private:
    //动态数组
    T* _data;

    //最大容量
    size_t _capacity;

    //当前数量
    size_t _size;
};

我们这里开了一个动态数组：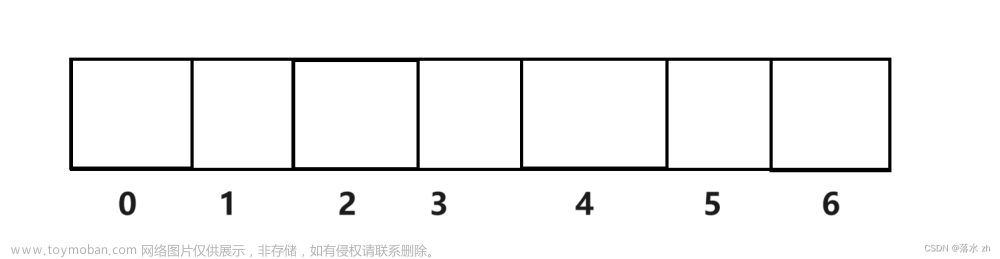

我们一般想象的栈是竖着的，我们可以把这个数组倒一头：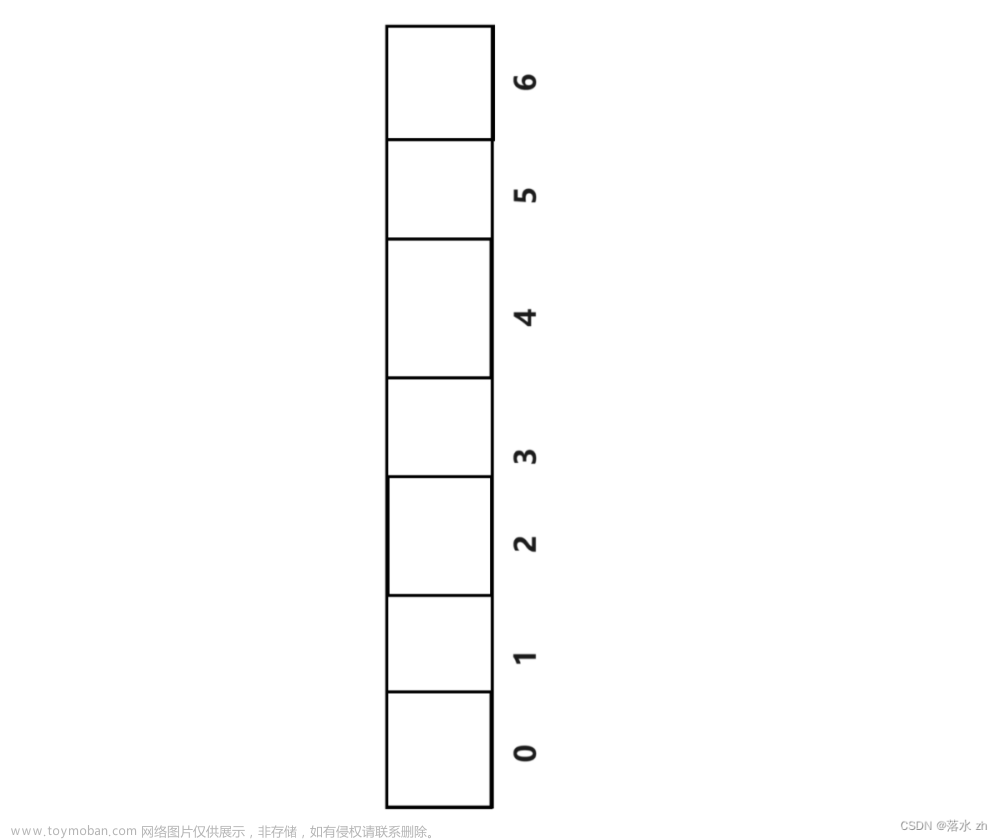

然后我们可以用一个_size的下标，指向我们0号位置（这里的下标有妙用）：

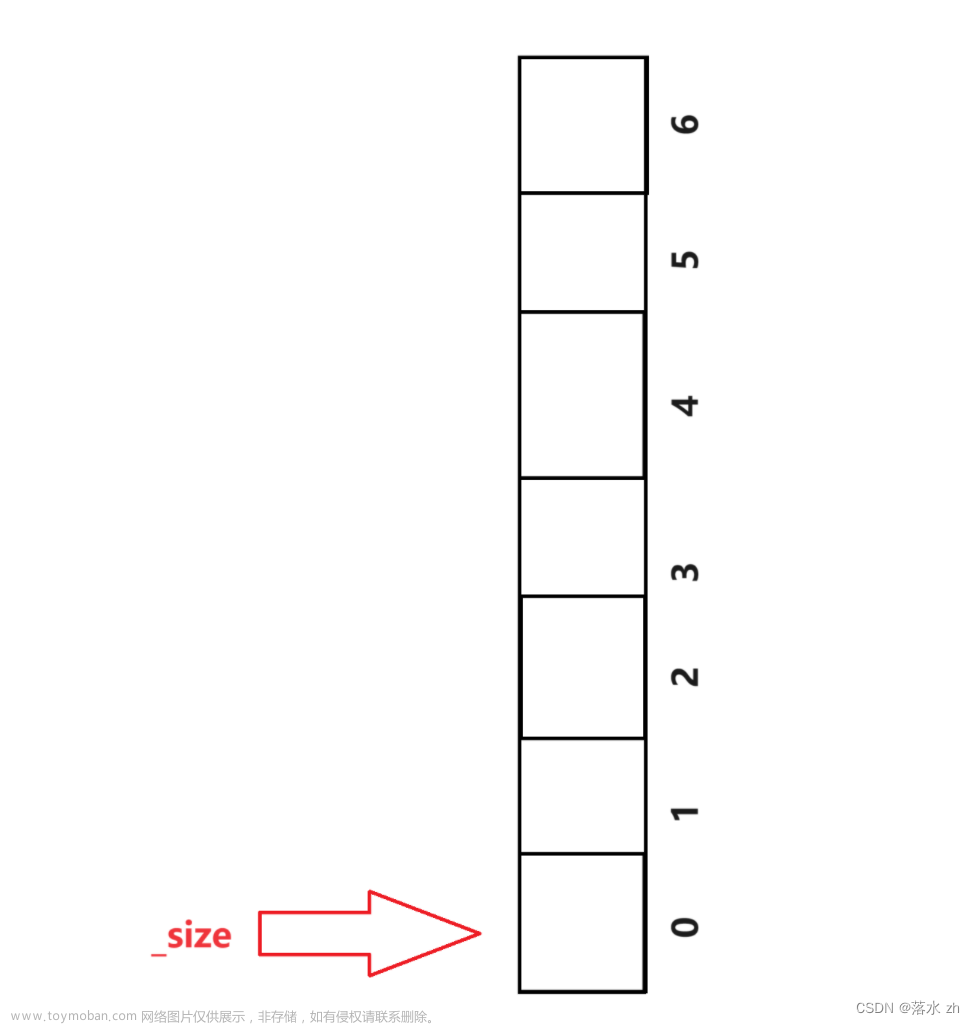
如果有元素入栈，我们先入栈：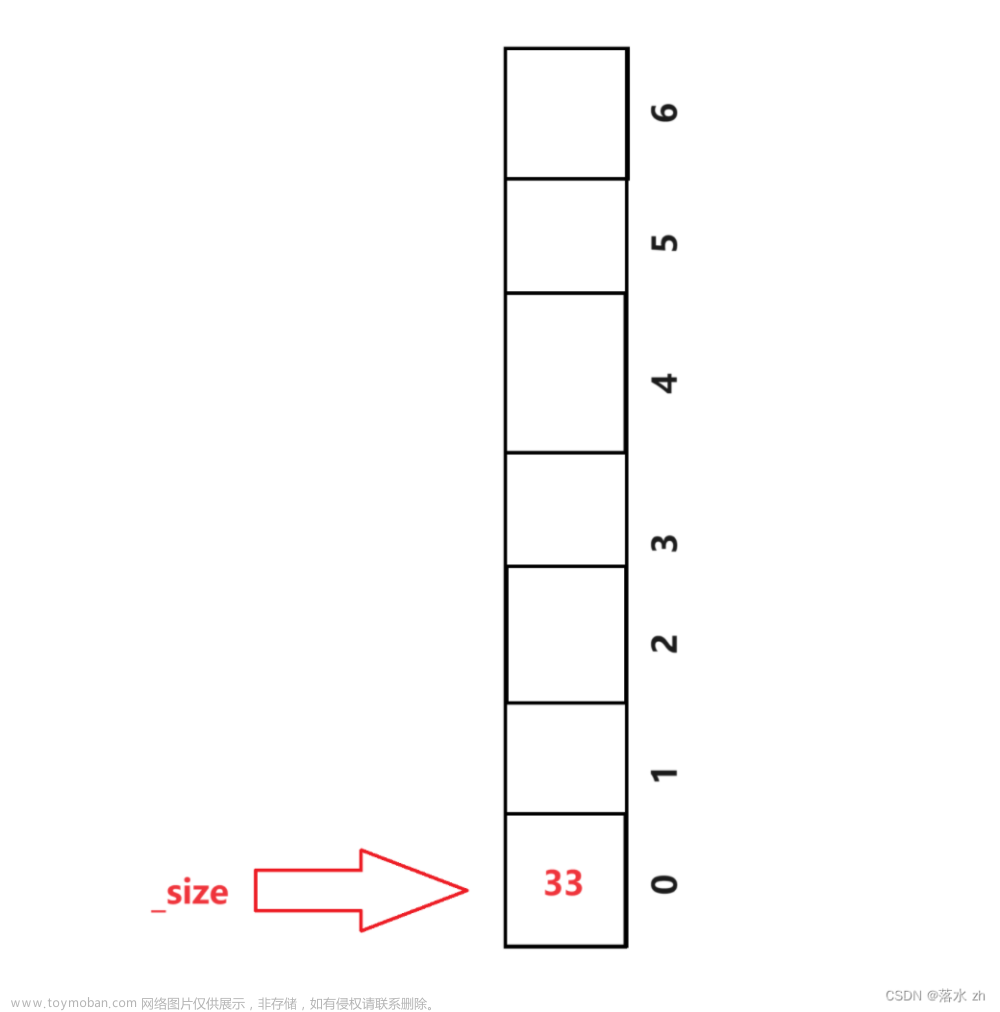

_size加一：

模拟这样的行为，我们发现_size总是指向栈顶位置的下一个的位置，但是又因为数组的下标又是从0开始，_size也可以表示栈中有多少个元素。

我们可以用这样的特性，来实现push和top和pop：

    //push
    void push(const T& data)
    {
        assert(_size < _capacity);

        _data[_size++] = data; //在_data[_size]放入之后，_size+1，指向下一个位置
    }

    //pop
    const T& pop()
    {
        assert(_size != 0);

        return _data[--_size]; //因为_size指向栈顶元素的下一个位置，首先先减一取到栈顶
    }

    //top
    const T& top()
    {
        assert(_size != 0);

        return _data[_size - 1];
    }

既然这里的_size是指向栈顶元素的下一个位置，我们也可以让_size指向栈顶元素，这样_size的初始位置就得从-1开始：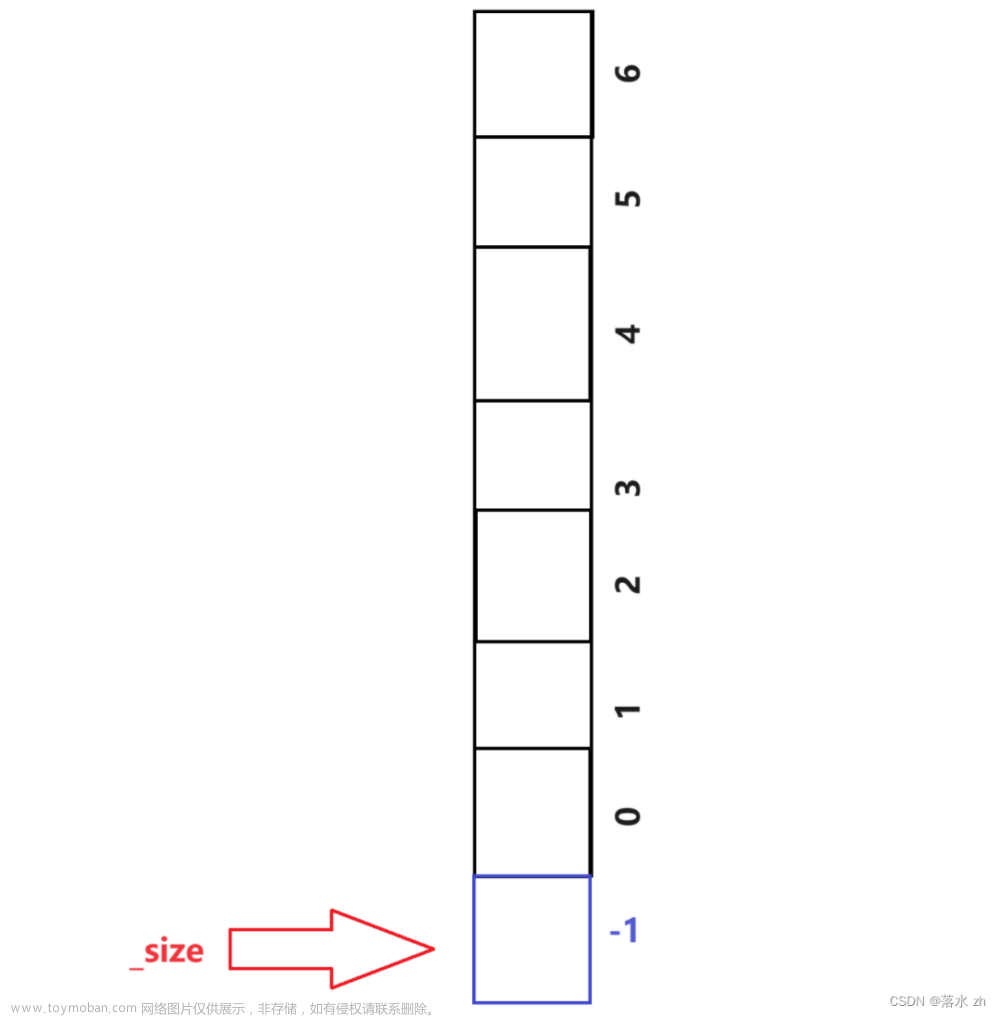
这样元素入栈，首先要加一（防止下标越界）
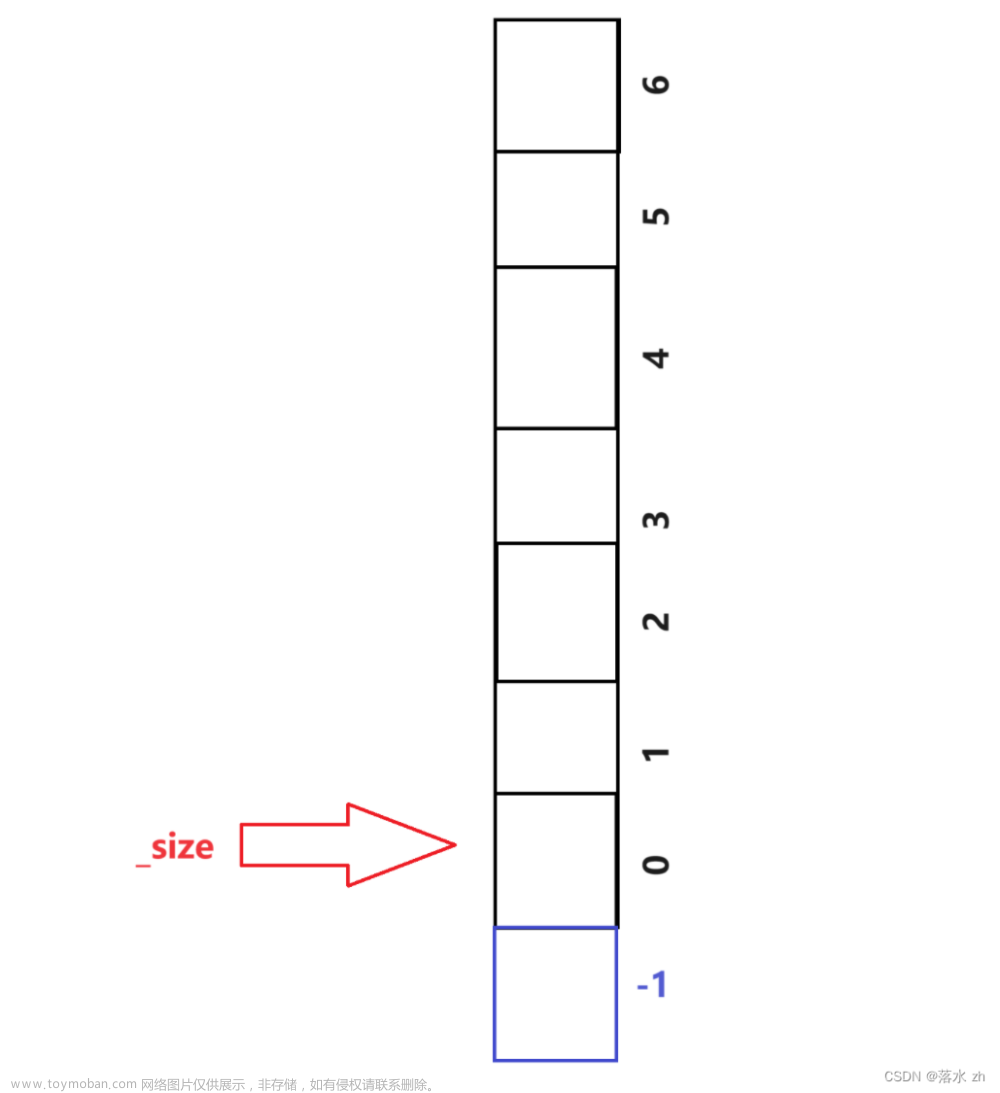然后再放入元素：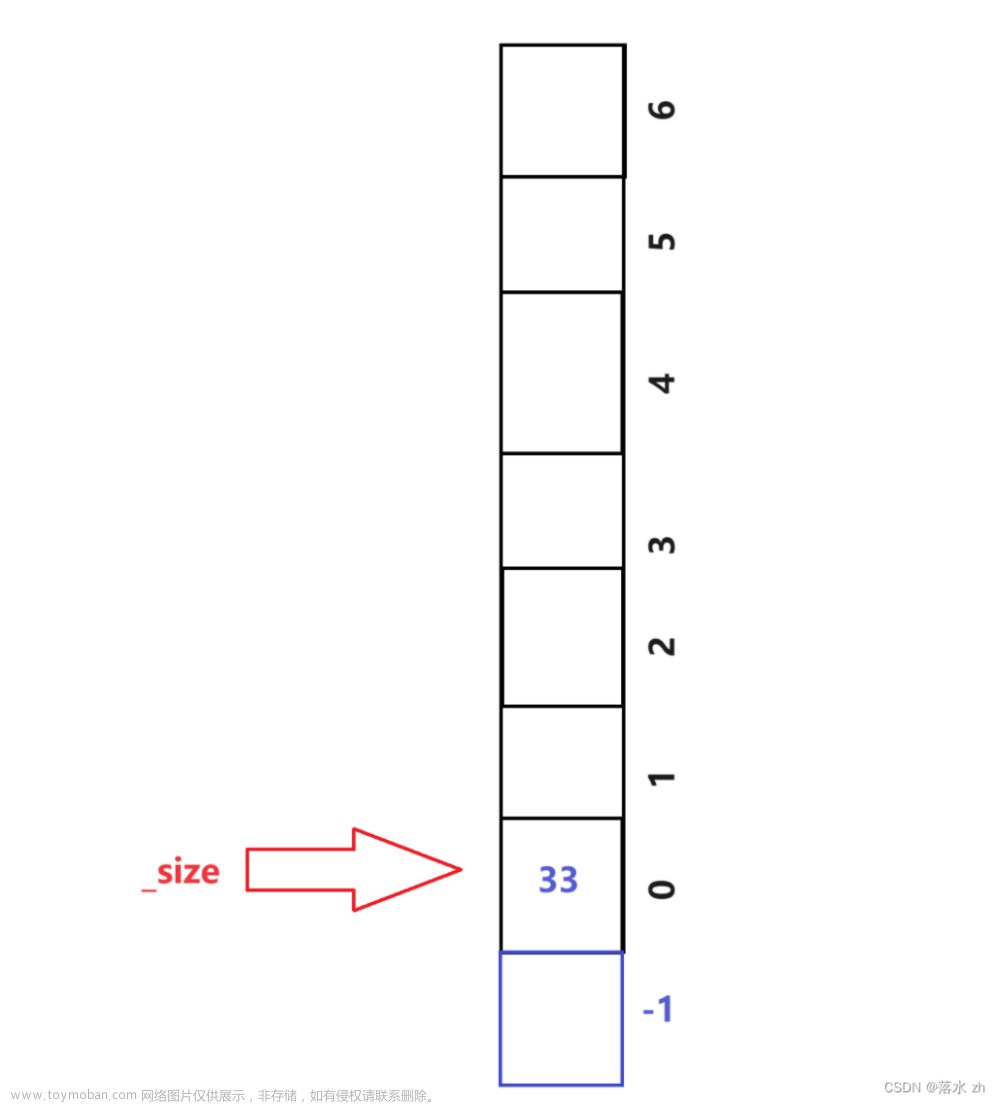

大家可以根据这个写一下这个版本的栈，这里不再赘述。

顺序栈的实现

下面是完整顺序栈的实现：

#pragma once
#include <cassert>
#include <iostream>

template <class T>
class MyStack
{
public:
    // 无参构造函数，使用默认容量创建栈
    MyStack()
        : _capacity(10)
        , _size(0)
    {
        // 开辟空间，创建动态数组，初始容量为 _capacity
        _data = new T[_capacity];
    }

    // 带参构造函数，根据指定容量创建栈
    MyStack(const size_t& capacity)
        : _capacity(capacity)
        , _size(0)
    {
        // 开辟空间，创建动态数组，容量为传入的 _capacity
        _data = new T[_capacity];
    }

    // 压栈操作，将新元素添加到栈顶
    void push(const T& data)
    {
        // 断言检查当前栈是否已满，若已满则抛出断言失败
        assert(_size < _capacity);

        // 将新元素存入动态数组的当前位置，并递增栈大小
        _data[_size++] = data;
    }

    // 出栈操作，删除栈顶元素并返回其值
    const T& pop()
    {
        // 断言检查当前栈是否为空，若为空则抛出断言失败
        assert(_size != 0);

        // 返回栈顶元素的值，并递减栈大小
        return _data[--_size];
    }

    // 查看栈顶元素的值，不改变栈状态
    const T& top()
    {
        // 断言检查当前栈是否为空，若为空则抛出断言失败
        assert(_size != 0);

        // 返回栈顶元素的值（动态数组的最后一个元素）
        return _data[_size - 1];
    }

    // 判断栈是否为空
    bool empty()
    {
        // 返回当前栈大小是否为0，即栈是否为空
        return _size == 0;
    }

    // 返回栈中元素数量
    size_t size()
    {
        // 返回当前栈大小（元素数量）
        return _size;
    }

private:
    // 动态数组，用于存储栈中的元素
    T* _data;

    // 最大容量，即动态数组的容量
    size_t _capacity;

    // 当前数量，即栈中元素的数量
    size_t _size;
};

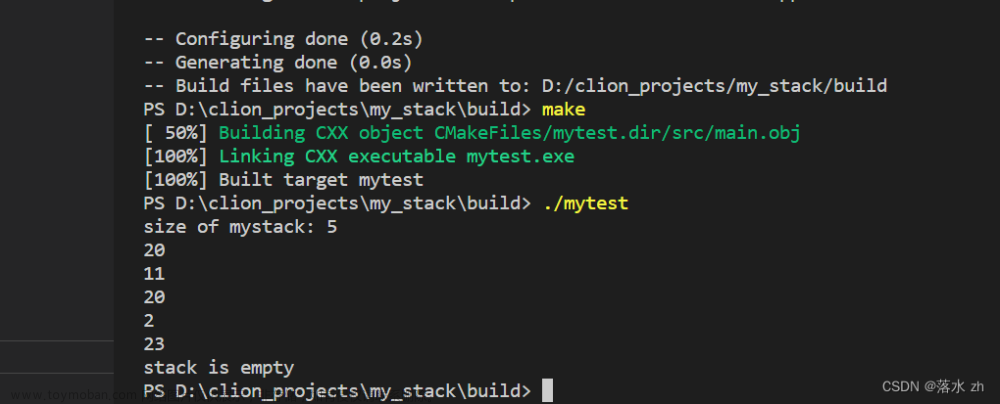
我们可以测试一下：

#include"my_stack.h"

int main()
{
    MyStack<int> mystack;

    mystack.push(23);
    mystack.push(2);
    mystack.push(20);
    mystack.push(11);
    mystack.push(20);

    std::cout<<"size of mystack: "<<mystack.size()<<std::endl;
   
   
    while(!mystack.empty())
    {
        std::cout<<mystack.pop()<<std::endl;
    }

    if(mystack.empty()==true)
    {
        std::cout<<"stack is empty"<<std::endl;
    }


    return 0;
}

链栈的实现

上面我们使用的是数组来模拟实现的栈，我们也可以用链表来模拟栈（我这里用带尾指针双向链表来模拟）：

我们还是定义一个结点类：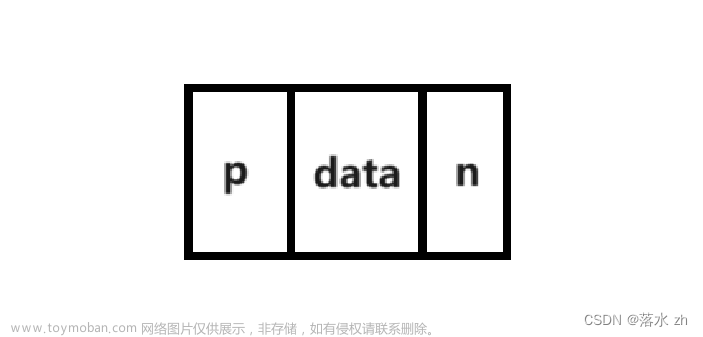

//结点类
template<class T>
struct Node
{
   Node()
    :_data(T())
    ,_next(nullptr)
    ,_prve(nullptr)
   {

   }

   Node(const T& data)
    :_data(data)
    ,_next(nullptr)
    ,_prve(nullptr)
   {

   }
  //数据域
  T _data;

  //指针域
  Node<T>* _next;
  Node<T>* _prve;
};

这是单链表中的结构：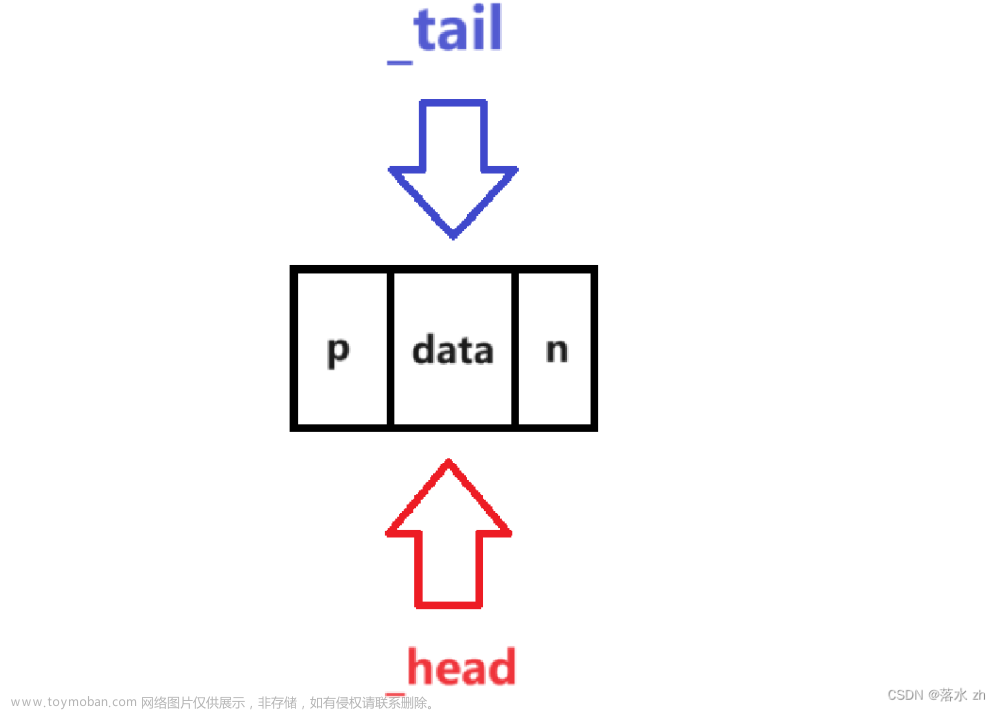

我们可以稍微改一下名字：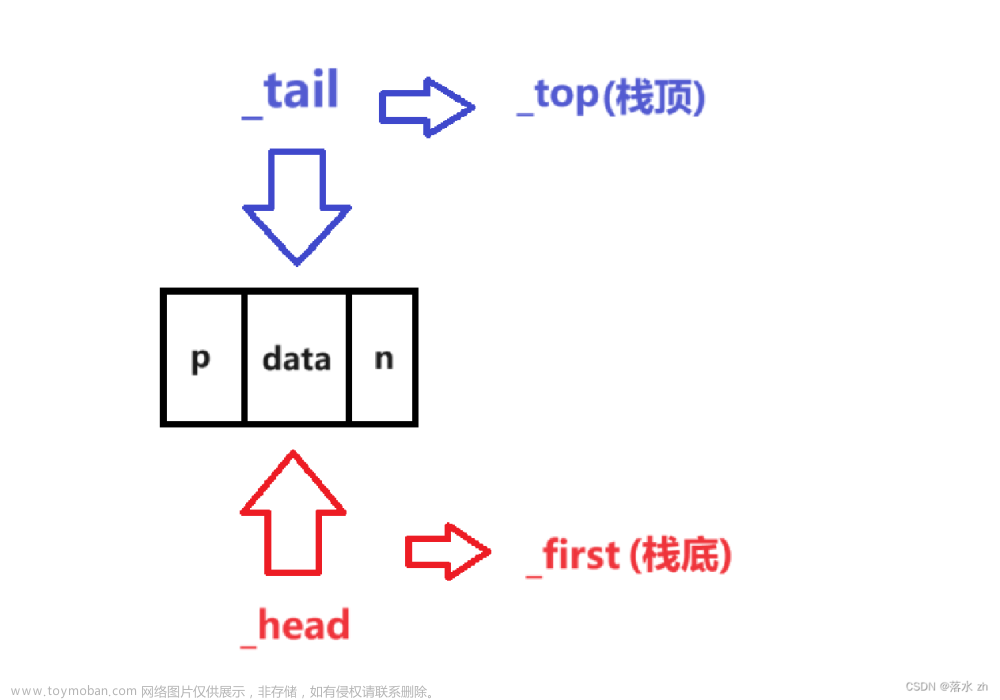

在这里我没有用带头结点的双向链表，所以一开始_top和_first会指向nullptr：

等要插入时，才插入第一个结点：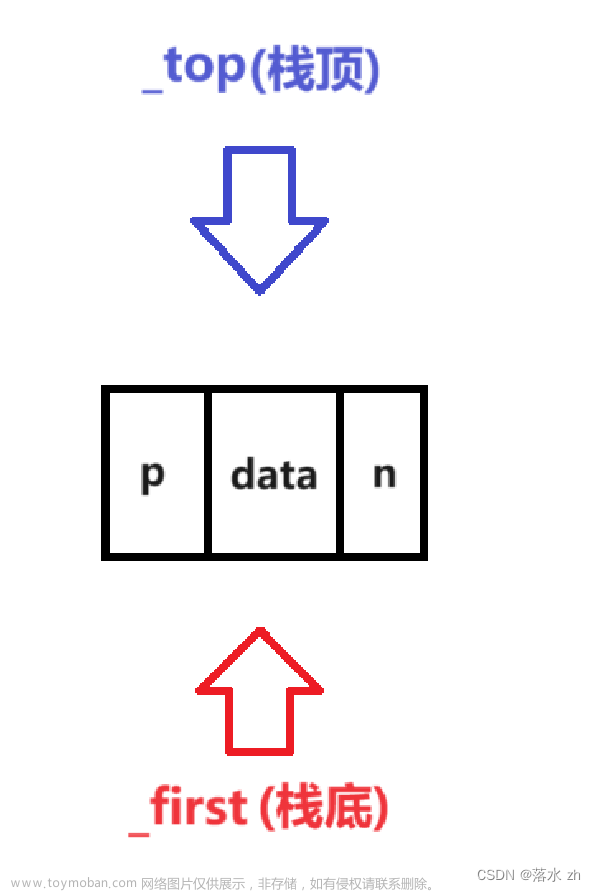

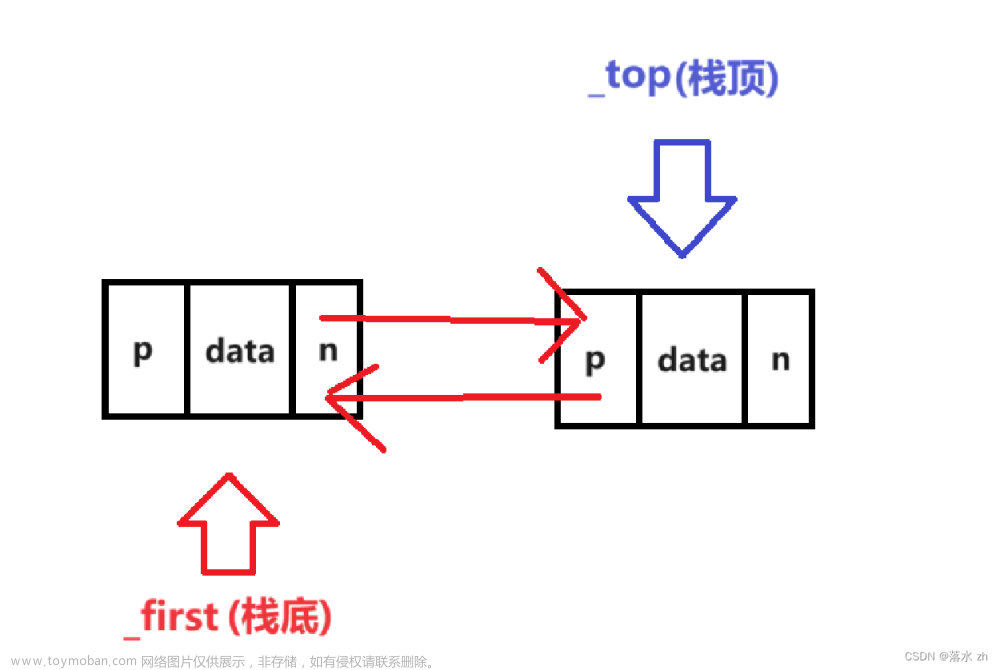
void push(const T& data)
{
    // 当栈为空时，直接创建新的节点作为栈的第一个元素和栈顶元素
    if (_first == nullptr)
    {
        _first = new _Node(data);
        _top = _first;
    }
    // 当栈非空时，创建新节点并插入到链表末尾，更新栈顶指针
    else
    {
        _Node* newnode = createNode(data); // 创建新节点
        // 更新链表结构：将新节点的 _prve 指针指向当前栈顶节点
        newnode->_prve = _top;

        // 将当前栈顶节点的 _next 指针指向新节点
        _top->_next = newnode;

        // 更新栈顶指针，使新节点成为新的栈顶元素
        _top = newnode;
    }
    // 增加栈大小
    _size++;
}

下面是完整代码：

#pragma once
#include<iostream>

// 结点类
template<class T>
struct Node
{
   // 默认构造函数，初始化数据和指针为默认值
   Node()
    : _data(T())
    , _next(nullptr)
    , _prve(nullptr)
   {}

   // 带参构造函数，根据给定数据初始化结点
   Node(const T& data)
    : _data(data)
    , _next(nullptr)
    , _prve(nullptr)
   {}

   // 数据域，存储链栈中实际的元素值
   T _data;

   // 指针域，分别指向下一个结点和前一个结点
   Node<T>* _next;
   Node<T>* _prve;
};

// 链栈类
template<class T>
class MyStack 
{
    // 内部类型定义，简化代码中的类型书写
    typedef Node<T> _Node;

public:
    // 构造函数，初始化栈为空
    MyStack()
        : _first(nullptr)
    {
        _top = _first;
    }

    // 创建结点
    _Node* createNode(const T& data)
    {
        _Node* newnode = new _Node(data);

        if (newnode == nullptr)
        {
            exit(EXIT_FAILURE); // 如果内存分配失败，直接终止程序
        }

        return newnode;
    }

    // 压栈操作，将新元素添加到栈顶
    void push(const T& data)
    {
        if (_first == nullptr) // 当栈为空时
        {
            _first = new _Node(data); // 创建新节点作为栈的第一个元素和栈顶元素
            _top = _first;
        }
        else // 当栈非空时
        {
            _Node* newnode = createNode(data); // 创建新节点

            // 更新链表结构：将新节点的 _prve 指针指向当前栈顶节点
            newnode->_prve = _top;
            // 将当前栈顶节点的 _next 指针指向新节点
            _top->_next = newnode;

            // 更新栈顶指针，使新节点成为新的栈顶元素
            _top = newnode;
        }

        // 增加栈大小
        _size++;
    }

    // 出栈操作，删除栈顶元素并返回其值
    T pop()
    {
        T top = _top->_data; // 保存栈顶元素的值

        if (_top == _first) // 当栈只剩一个元素时
        {
            delete _top; // 删除栈顶元素
            _top = nullptr;
            _first = nullptr; // 清空栈
        }
        else // 当栈中有多个元素时
        {
            _Node* prve = _top->_prve; // 获取栈顶元素的前一个结点

            prve->_next = nullptr; // 断开与已删除节点的连接
            delete _top; // 删除栈顶元素

            _top = prve; // 更新栈顶指针
        }

        // 减小栈大小
        --_size;
        return top; // 返回栈顶元素的值
    }

    // 查看栈顶元素的值，不改变栈状态
    const T& top() const
    {
        return _top->_data;
    }

    // 判断栈是否为空
    bool empty() const
    {
        return _size == 0;
    }

    // 返回栈中元素数量
    size_t size() const
    {
        return _size;
    }

private:
    // 第一个结点，用于初始化栈
    _Node* _first = nullptr;

    // 栈顶指针，始终指向栈顶元素
    _Node* _top;

    // 当前元素数量，表示栈大小
    size_t _size = 0;
};

测试一下：

//#include"my_stack_sequence.h"
#include"my_stack_link.h"

int main()
{
    MyStack<int> mystack;

    mystack.push(23);
    mystack.push(2);
    mystack.push(20);
    mystack.push(11);
    mystack.push(20);

    std::cout<<"size of mystack: "<<mystack.size()<<std::endl;
   
    while(!mystack.empty())
    {
        std::cout<<mystack.pop()<<std::endl;
    }
    
    if(mystack.empty()==true)
    {
        std::cout<<"stack is empty"<<std::endl;
    }


    return 0;
}

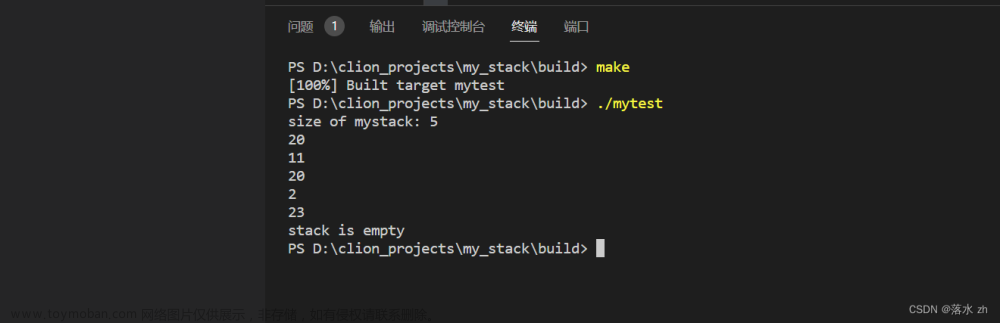文章来源地址https://www.toymoban.com/news/detail-861592.html

到了这里，关于数据结构——栈（C++实现）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！