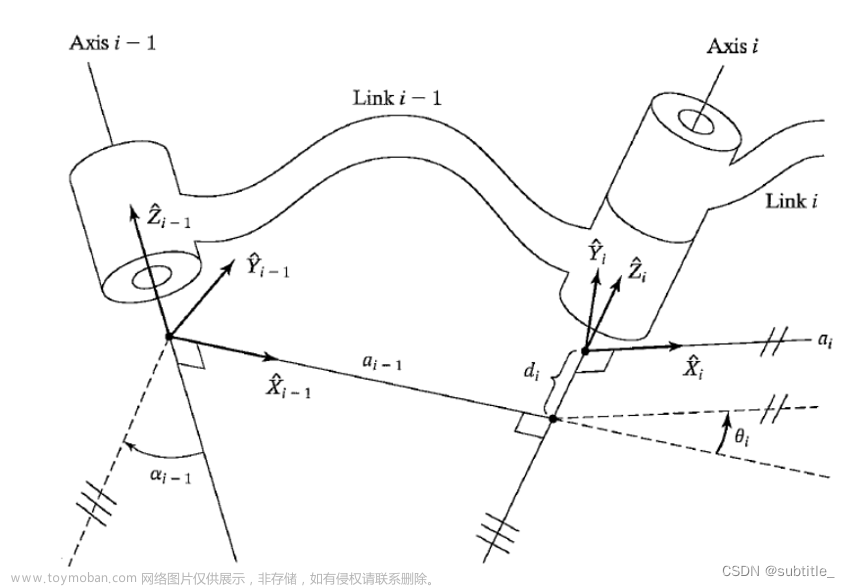
从线性变换的角度理解机器人坐标变换



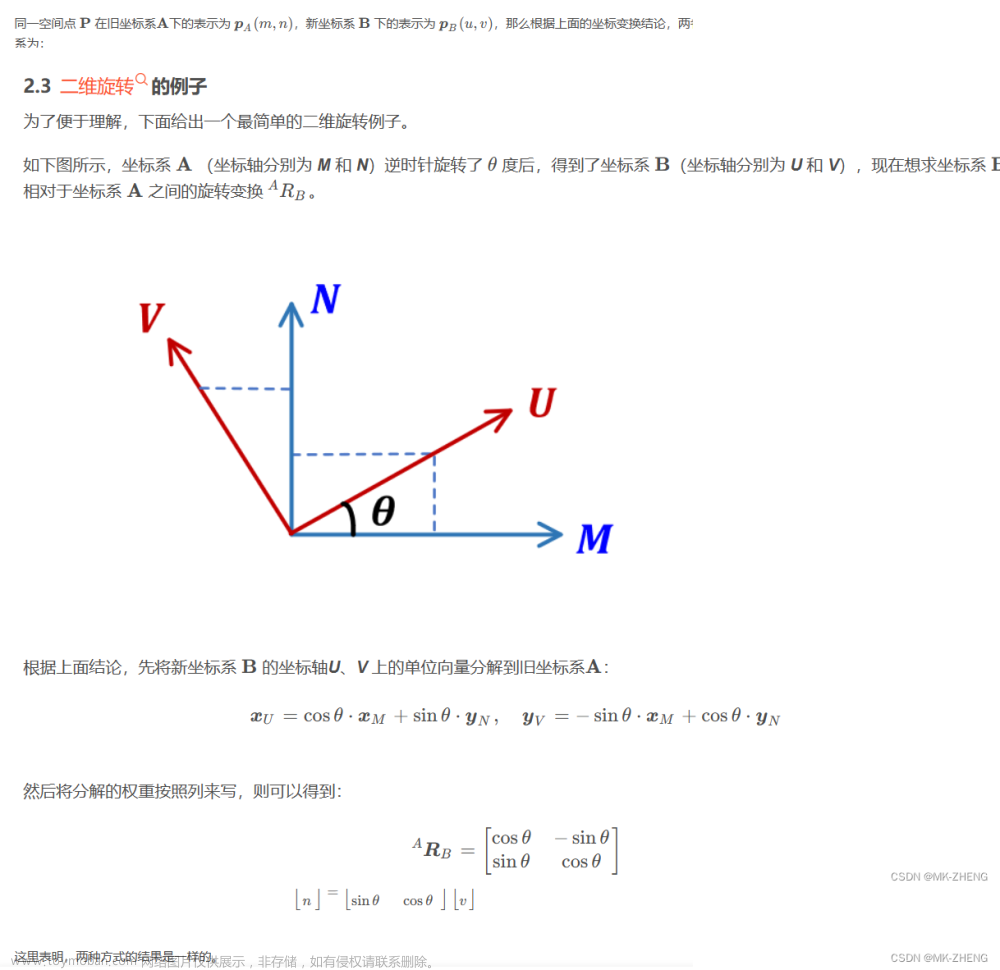

实际应用:
- 为什么要标定旋转中心
在机器视觉实际应用过程中,有这样的案例:机械手要抓取物料,物料每次的角度不一样,机械手的末端工具中心与其自身的旋转中心不重合,如果想完成这个抓取的工作,有两种解决方案:
方案一:TCP标定(Tool Center Point)
一般机械手都会有建立新工具坐标系的功能,比如EPSON。TCP标定的本质就是求旧的工具坐标系与新的工具坐标系的旋转平移矩阵。一般是定义新的工具编号,放一个参考点,多次旋转U轴(旋转轴)(4次),然后移动X,Y(base下)使新工具坐标末端对准参考点,对完之后点击示教就行了。
方案二:标定旋转中心和旋转半径
如果机器人没有TCP标定的功能怎么办呢?其实这种概率比较低,因为市场上几乎所有的机器人都会有这种功能了,大部分是由于操作机器人的工程师业务不够熟练,所以就把这个任务交给机器视觉工程师了。
还有另外一种情况,如果你使用的运动机构是运动控制卡控制的,这里我们讨论的是有旋转轴的机构,而且旋转轴上的工具末端中心又和旋转轴不重合,这时候就不得不标定旋转中心和旋转半径了。
其实一般带有旋转轴的机构,我们都会标定旋转中心的,因为靠机械定位误差比较大,机器视觉工程师要对最终的精度负责,标定旋转中心是必要的,要不然我们要旋转轴干嘛呢? - 如何标定旋转中心
2.1 标定旋转中心的操作步骤
如下图,在旋转轴工具上放置一个Mark点,旋转角度,获得三个点,三点拟合圆,获得圆心坐标和旋转半径(默认已经做完九点标定,这三个点转为世界坐标后再计算圆心坐标和旋转半径)。
2.2 三点拟合圆心代码:
通过下面的计算,我们能得到旋转中心和旋转半径。
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace 求圆心
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
double[] xy = new double[3];
xy = RotateCenter(double.Parse(txtX1.Text),double.Parse(txtY1.Text),double.Parse(txtX2.Text),double.Parse(txtY2.Text),double.Parse(txtX3.Text),double.Parse(txtY3.Text));
txtxcen.Text = xy[0].ToString();//X
txtycen.Text = xy[1].ToString();//Y
txtrcen.Text = xy[2].ToString();//R
}
public double[] RotateCenter(double x1,double y1,double x2,double y2,double x3,double y3)
{
double a, b, c, d, e, f;
a = 2 * (x2-x1);
b = 2 * (y2-y1);
c = x2 * x2 + y2 * y2 - x1 * x1 - y1 * y1;
d = 2 * (x3 - x2);
e = 2 * (y3 - y2);
f = x3 * x3 + y3 * y3 - x2 * x2 - y2 * y2;
double x = (b * f - e * c) / (b*d-e*a);
double y = (d*c-a*f) / (b*d-e*a);
double r = Math.Sqrt((x1 - x) * (x1 - x) + (y1 - x) * (y1 - x));
double[] xyr = new double[3];
xyr[0] = x;
xyr[1] = y;
xyr[2] = r;
return xyr;
}
}
}
- halcon多点拟合圆的方法
如果你使用的算法库是halcon,那么我将给您提供一个更方便的多点拟合圆的方法:
利用Halcon将多个点拟合成圆
halcon代码
Row := [0,100.5,100,3]
Col := [4,0,100,99.4]
gen_contour_polygon_xld (Contour, Row, Col)
fit_circle_contour_xld (Contour, 'geotukey', -1, 0, 0, 3, 2, Row_C, Column_C, Radius_C, StartPhi_C, EndPhi_C, PointOrder_C)
dev_set_color ('blue')
gen_circle_contour_xld (ContCircle, Row_C, Column_C, Radius_C, 0, 4 * acos(0), 'positive', 1)
-
如何使用旋转中心计算偏移量
这一步就是最重要的一步了,如何使用旋转中心和旋转半径来确定偏移量呢?


-
计算一点绕另一点旋转一定角度后新点的坐标
第4节主要是为了讲清楚这个推导过程,接下来我们直接给出代码:文章来源:https://www.toymoban.com/news/detail-861708.html
using System;
namespace RotatePoint
{
class Program
{
static void Main(string[] args)
{
double X = 0;
double Y = 0;
//顺时针角度为负数
RotateAngle(1, 1, -45, 2, 2, ref X, ref Y);
Console.WriteLine(X+","+Y);
Console.ReadKey();
}
public static string RotateAngle(double XRotation, double YRotation, double ARotate, double XBefore, double YBefore, ref double XAfter, ref double YAfter)
{
try
{
double Rad = 0;
Rad = ARotate * Math.Acos(-1) / 180;
XAfter = (XBefore - XRotation) * Math.Cos(Rad) - (YBefore - YRotation) * Math.Sin(Rad) + XRotation;
YAfter = (YBefore - YRotation) * Math.Cos(Rad) + (XBefore - XRotation) * Math.Sin(Rad) + YRotation;
return "OK";
}
catch (Exception ex)
{
return ex.Message;
}
}
}
}
标定旋转中心的目的就是,计算旋转一定角度后新点的坐标;
X,Y和角度纠偏的步骤:
X,Y和角度的偏差,在机械动作上是同时进行纠偏的,但是在算法中却不是,我们往往是先转正角度,然后算出转正角度后新位置的坐标;
此时新位置和模板角度是相同的,只需要平移就能重合,这个平移量就是9点标定时算出并保存的仿射变换矩阵来计算的了。文章来源地址https://www.toymoban.com/news/detail-861708.html
到了这里,关于【机器人学】一、从线性变换的角度理解机器人坐标变换的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!