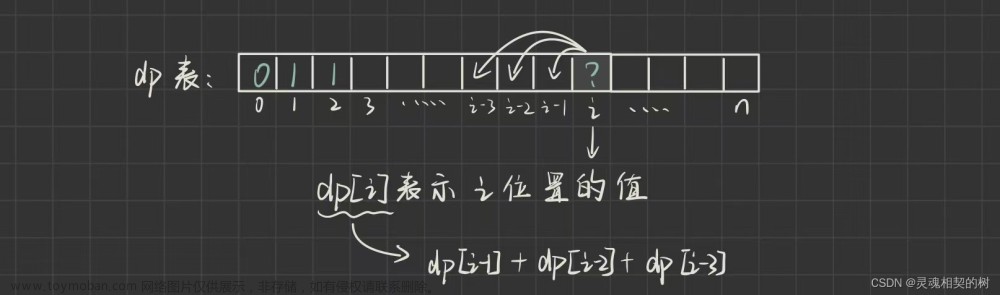
动态规划的思想:将一个问题分隔为若干个子问题,完成子问题得到结构再得到最终的答案
动态规划往往解题步骤固定,分为以下几步
1.找出状态表示
2.完成状态转移方程
3.初始化
4.填表顺序
5.返回值
后面三步偏重细节,二解题的核心就在于前两步,所以要想练好动态规划,大量的练习,见识更多的题型无疑是很重要的,下面我们开始今天的练习
1.第N个泰波那契数
1137. 第 N 个泰波那契数
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值
这道题目很简单,旨在让我们熟悉动态规划的解题步骤,下面我们展开分析
1.状态表示:用dp[ i ]表示第 i 个泰波那契数
2.状态转移方程:dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3 ]
3.初始化:dp[0] = 0; dp[1] = 1; dp[2] = 1
4.填表顺序:从左往右依次填
5.返回值:dp[n]
当然我们要注意边缘数据的特殊处理,不然会出现越界的情况
class Solution {
public:
int tribonacci(int n)
{
//1. 创建dp表
//2. 初始化
//3. 填表
//4. 返回值
//边缘数据处理
if(n == 0 || n == 1) return n;
if(n == 2) return 1;
vector<int> dp(n + 1);
dp[0] = 0; dp[1] = 1; dp[2] = 1;
for(int i = 3; i <= n; ++i)
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
return dp[n];
}
};这是ac代码
2.三步问题
面试题 08.01. 三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007
1.状态表示:用dp[ i ]表示上到第i个台阶的可能方式
2.状态转移方程:dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3 ]
3.初始化:dp[0] = 0; dp[1] = 1; dp[2] = 1
4.填表顺序:从左往右依次填
5.返回值:dp[n]
这里要注意数据的处理,因为数据很大,每一次相加之后都要对题给数据取模
class Solution {
public:
int waysToStep(int n)
{
const int MOD = 1e9 + 7;
if(n == 1 || n == 2) return n;
vector<int> dp(n + 1);
dp[0] = 1; dp[1] = 1; dp[2] = 2;
for(int i = 3; i <= n; ++i)
dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + + dp[i - 3]) % MOD;
return dp[n];
}
};这是ac代码
3.使用最小花费爬楼梯
LCR 088. 使用最小花费爬楼梯
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当爬上一个阶梯都要花费对应的体力值,一旦支付了相应的体力值,就可以选择向上爬一个阶梯或者爬两个阶梯。
请找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯
1.状态表示:用dp[ i ]表示上到第i个阶梯需要的最小费用
2.状态转移方程:dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
3.初始化:dp[0] = 0; dp[1] = 0;
4.填表顺序:从左往右依次填
5.返回值:dp[n]
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost)
{
int n = cost.size();
vector<int> dp(n + 1);
dp[0] = 0; dp[1] = 0;
for(int i = 2; i <= n; ++i)
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
return dp[n];
}
};这是ac代码
4.解码方法
91. 解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> "1"
'B' -> "2"
...
'Z' -> "26"
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法
1.状态表示:用dp[ i ]表示上到第i - 1个字母最大解码方法
2.状态转移方程:dp[i] = dp[i - 1] + dp[i - 2](要判断是否存在该情况)
3.初始化:dp[0] = 1; dp[1] = s[0] != '0';
4.填表顺序:从左往右依次填
5.返回值:dp[n]
class Solution {
public:
int numDecodings(string s)
{
int n = s.size();
vector<int> dp(n + 1);
dp[0] = 1;
dp[1] = s[0] != '0';
for(int i = 2; i <= n; ++i)
{
if(s[i - 1] != '0') dp[i] += dp[i - 1];
int num = (s[i - 2] -'0') * 10 + s[i - 1] - '0';
if(num >= 10 && num <= 26) dp[i] += dp[i - 2];
}
return dp[n];
}
};这是ac代码文章来源:https://www.toymoban.com/news/detail-861748.html
新手写博客,有不对的位置希望大佬们能够指出,也谢谢大家能看到这里,让我们一起学习进步吧!文章来源地址https://www.toymoban.com/news/detail-861748.html
到了这里,关于动态规划专训1——泰波那契数列模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!