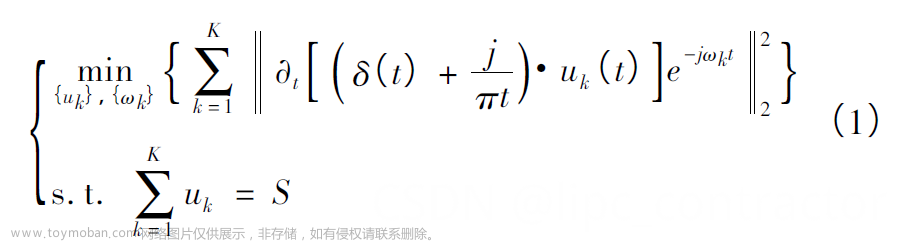低秩分解综述
-
5.4 满秩分解
任意矩阵都有满秩分解 Full rank factorization 。也就是说不限于方阵,更不限于满秩矩阵。满秩分解用途很广,尤其是后期的对于广义逆的学习来说非常重要。 首先要搞清楚什么是满秩分解 full rank factorization ,假设矩阵为 A A A ,它的秩为 r r r ,满秩分解就是分解为如下
-
变分模态分解(VMD)
在信号处理中,变分模态分解是一种信号分解估计方法。该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心和带宽,从而能够自适应地实现信号的频域剖分及各分量的有效分离。 VMD(Variational mode decomposition)是一种自适应、完全非递归的
-
SVD分解示例
帮助到你了就点个赞吧! Powered By Longer-站在巨人的肩膀上 对矩阵A进行SVD分解的公式:。其中A可以不是方阵,是左奇异矩阵,是右奇异矩阵。其中V是的特征向量(注意公式中V有个转置操作),U是的特征向量。是对角阵,对角元素是U、V的共同特征值,例如有三个特征值时:
-
矩阵分析:特征值分解
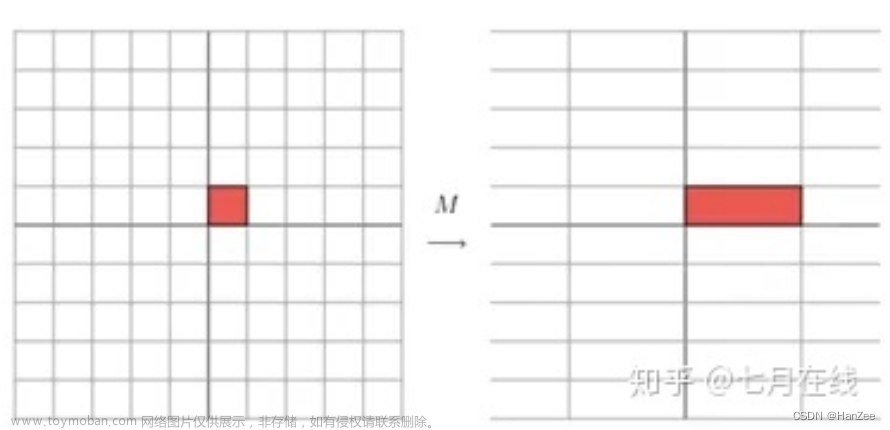
伸缩 一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵: 因为这个矩阵M乘以一个向量(x,y)的结果是: 旋转 除了伸缩变换,也可以进行旋转变换。 上面的矩阵是对称的,所以这个变
-
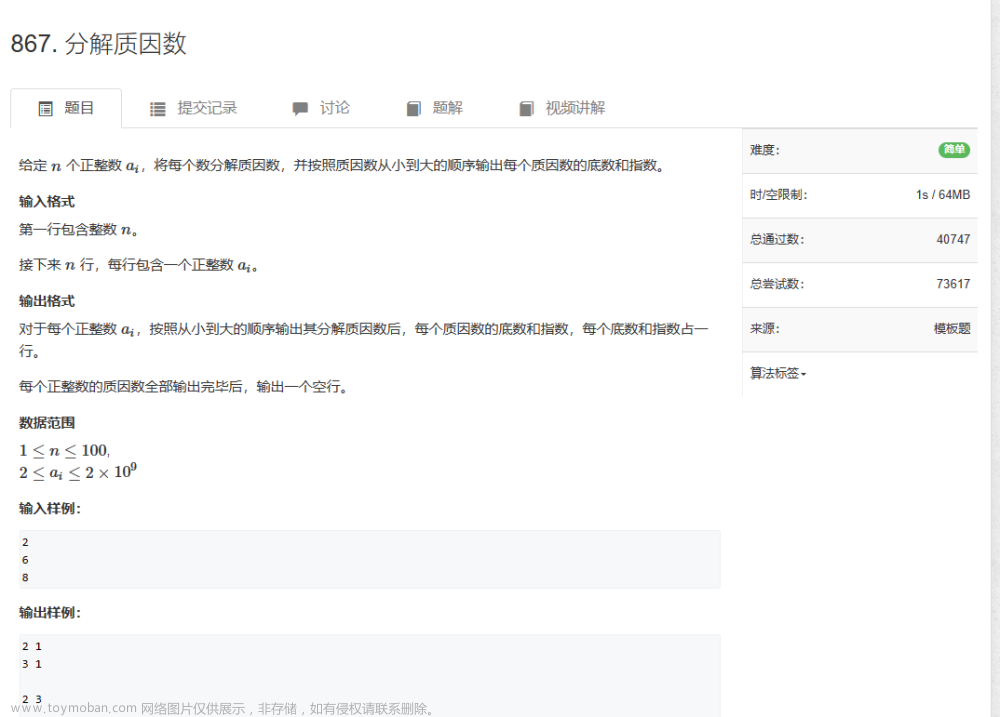
分解质因数--试除法
但是按照题意我们需要的是枚举质因数,然后呢我们枚举的是 1到n ,这个时候我们就会考虑一个问题,就是1到n这个里面就是不只有质数,还有合数,这个是我们担心的一个问题. 我们来说明一下这个情况 为什么我们枚举这个1-n是可以行的 ..........................................
-
LU分解(C++)
LU分解是一种重要的数值线性代数技术, 用于解决线性方程组和矩阵求逆等问题. 在科学工程领域, 经常需要解决形如 A x = b Ax = b A x = b 的线性方程组, 其中 A A A 是系数矩阵, x x x 是未知向量, b b b 是已知向量. LU分解是一种将系数矩阵 A A A 分解为一个下三角矩阵 L L L 和一个上三
-
6.10 谱分解
单纯矩阵 normal matrix 指的是符号 A T A = A A T A^TA=AA^T A T A = A A T 的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。 对于单纯矩阵,存在以下的谱定理 Spectral theorem : 单纯矩阵可以分解为以下矩阵相加的形式: A = ∑ i = 1 n λ i v i v
-
6.12 谱分解
单纯矩阵 normal matrix 指的是符号 A T A = A A T A^TA=AA^T A T A = A A T 的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。 对于单纯矩阵,存在以下的谱定理 Spectral theorem : 单纯矩阵可以分解为以下矩阵相加的形式: A = ∑ i = 1 n λ i v i v
-
Python:分解质因数
把一个合数用质因数相乘的形式表示出来,叫做 分解质因数 . 分解质因数常见方法是短除法,也可以用Python实现. 给出三种分解质因数的代码:
-
矩阵分解及其Eigen实现
主要是用来记录自己的学习过程,内容也主要来自于网上的各种资料,然后自己总结而来,参考的资料都以注明,感谢这些作者的分享。如果内容有误,请大家指点。 定义 将矩阵等价为两个矩阵 L L L 和 U U U 的乘积 ,其中 L L L 和 U U U 分别是单位下三角矩阵和上三角
-
矩阵的奇异值分解
注:本博文为本人阅读论文、文章后的原创笔记,未经授权不允许任何转载或商用行为,否则一经发现本人保留追责权利。有问题可留言联系,欢迎指摘批评,共同进步!!! 假设矩阵 A mathbf{A} A 是一个 M × N M times N M × N 大小的矩阵。对其进行奇异值分解后可以得到: A
-
矩阵分析——矩阵分解
矩阵分解指的是将复杂的矩阵分解成比较简单的矩阵的乘积的形式。在数值代数、矩阵论和最优化应用。 三角分解: 矩阵的三角分解:将一个方阵 A pmb{A} A A 分解成一个下三角阵 L pmb{L} L L 和一个上三角矩阵 R pmb{R} R R 的乘积,即 A = L R pmb{A}=pmb{L}pmb{R} A A = L L R R 。 充分必
-
Mybatis分解式查询
目录 一、Mybatis一对多分解式查询 1. 新增持久层接口方法 2. 新增映射文件对应的标签 3. 新增测试方法 4. 运行效果 二、Mybatis一对
-
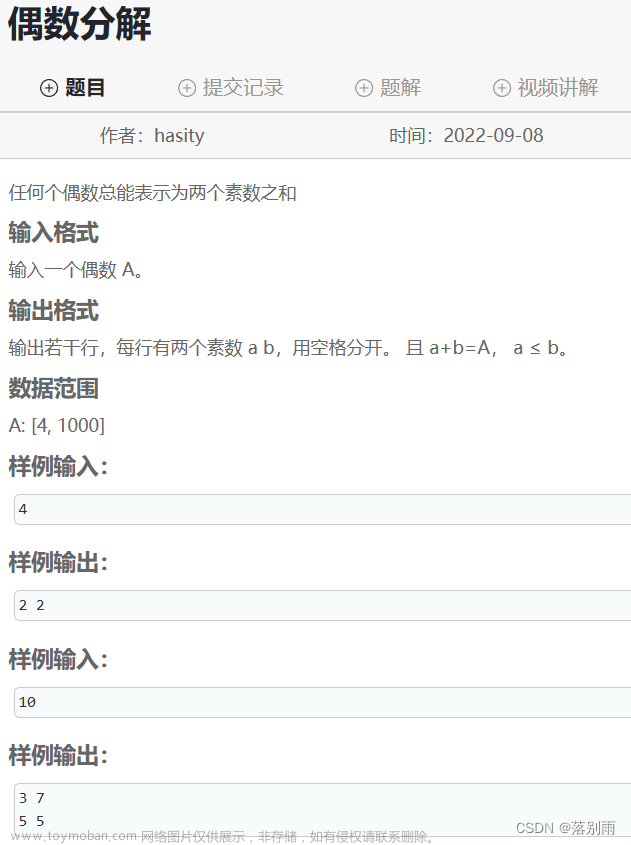
机试:偶数分解
题目描述: 代码示例: 运行结果:
-
11、矩阵的分解
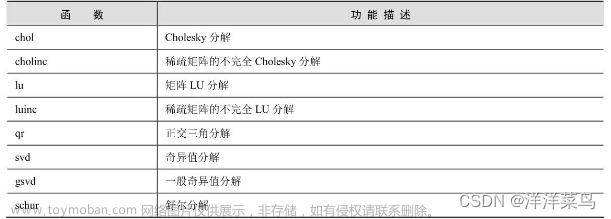
目录 一、对称正定矩阵的Cholesky分解 二、一般方阵的高斯消去法分解 三、矩形矩阵的正交分解 四、舒尔分解 矩阵分解 是把一个矩阵分解成几个“较简单”的矩阵连乘的形式。在MATLAB中矩阵分解的相关函数有: 在MATLAB中, 线性方程组的求解 主要基于4种基本的矩阵分解,即
-
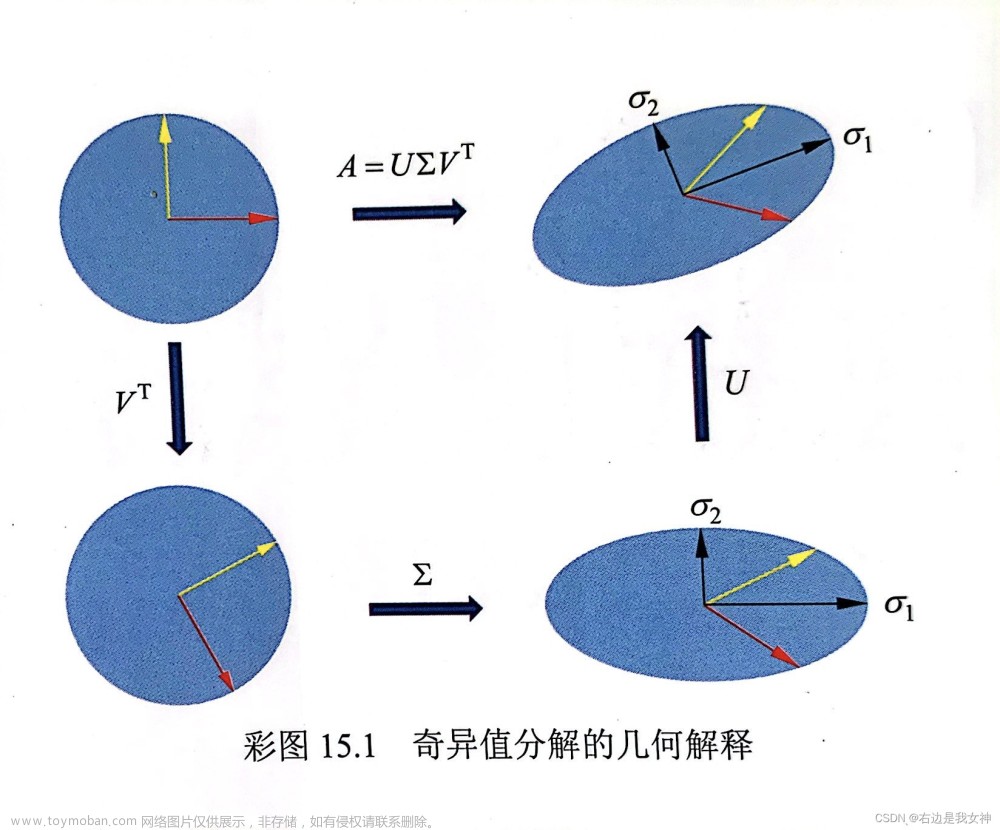
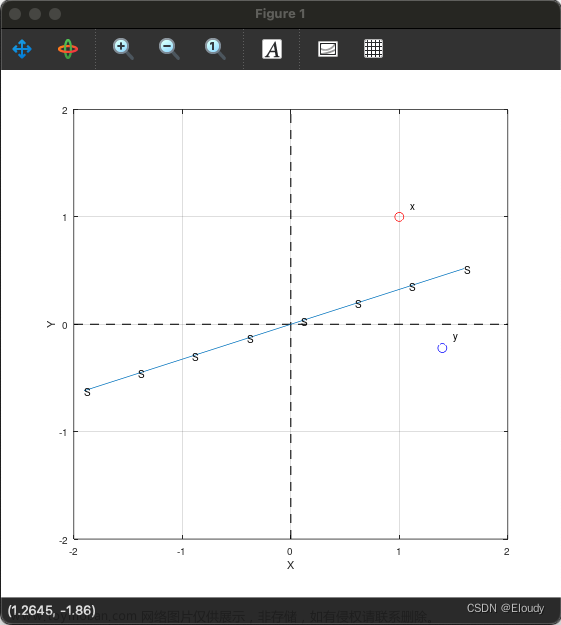
第十五章 奇异值分解
奇异值分解(SVD)是一种矩阵因子分解方法。 任意一个 m × n mtimes n m × n 矩阵,都可以表示为三个矩阵的乘积(因子分解)形式,分别是 n n n 阶正交矩阵、由降序排列的非负的对角线元素组成的 m × n mtimes n m × n 的矩形对角矩阵和 n n n 阶正交矩阵。 矩阵的奇异值分解一定
-
理顺 QR 分解算法
咱们网站的这个公式编辑器,估计是后台生成图片后贴回来的,固定分辨率而且分辨率不高。 还不如先离线 latex 生成 pdf 后再截图上来 When A and b are known, to solver the minimization of , where . The reduction of A to various canonical form via orthogonal transformations should use Householder reflections and
-
Lyndon分解 学习笔记
我们定义一个串是 (Lyndon) 串,当且仅当这个串的 最小后缀 就是这个串本身。 也就是说 (Lyndon) 串等价于这个串是它的所有循环表示中 字典序最小 的。 将一个字符串 (S) 分解为若干个子串: (s_1s_2s_3dots s_m) 。对于任意 (iin [1,m]) ,使得 (s_i) 为 (Lyndin) 串,且 (for
-
矩阵的分解
怎么计算矩阵又快又准——矩阵的分解 先判断Doolittle分解是否唯一,再进行Doolittle分解 各阶顺序主子式均不为0,Doolittle分解唯一; 特殊的:正定/负定矩阵,Doolittle分解唯一;严格行(列)对角占优矩阵,Doolittle分解唯一; Doolittle分解的算法 一共 5 种分解 【定义】Doolittle分解
-
大整数分解 浅析
解决:质因数分解大整数 n n n 。 1 ≤ n ≤ 1 0 18 1le nle 10^{18} 1 ≤ n ≤ 1 0 1 8 。 枚举 [ 2 , n ] [2,sqrt n] [ 2 , n ] 的所有质数,判断是否整除。除完之后只剩一个 质数 或者 1 1 1 了。时间复杂度 O ( n ln n ) O(dfrac{sqrt n}{ln n}) O ( ln n n ) 。 这是一个笨方法,但是它告诉我