低秩矩阵分解推荐
-
4.矩阵的分解
怎么计算矩阵又快又准——矩阵的分解 先判断Doolittle分解是否唯一,再进行Doolittle分解 各阶顺序主子式均不为0,Doolittle分解唯一; 特殊的:正定/负定矩阵,Doolittle分解唯一;严格行(列)对角占优矩阵,Doolittle分解唯一; Doolittle分解的算法 一共 5 种分解 【定义】Doolittle分解
-
矩阵分析:特征值分解
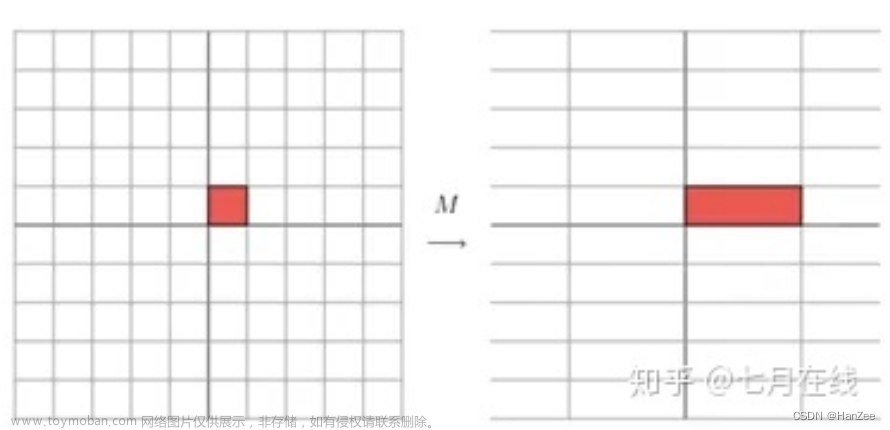
伸缩 一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵: 因为这个矩阵M乘以一个向量(x,y)的结果是: 旋转 除了伸缩变换,也可以进行旋转变换。 上面的矩阵是对称的,所以这个变
-
矩阵分解及其Eigen实现
主要是用来记录自己的学习过程,内容也主要来自于网上的各种资料,然后自己总结而来,参考的资料都以注明,感谢这些作者的分享。如果内容有误,请大家指点。 定义 将矩阵等价为两个矩阵 L L L 和 U U U 的乘积 ,其中 L L L 和 U U U 分别是单位下三角矩阵和上三角
-
矩阵的奇异值分解
注:本博文为本人阅读论文、文章后的原创笔记,未经授权不允许任何转载或商用行为,否则一经发现本人保留追责权利。有问题可留言联系,欢迎指摘批评,共同进步!!! 假设矩阵 A mathbf{A} A 是一个 M × N M times N M × N 大小的矩阵。对其进行奇异值分解后可以得到: A
-
11、矩阵的分解
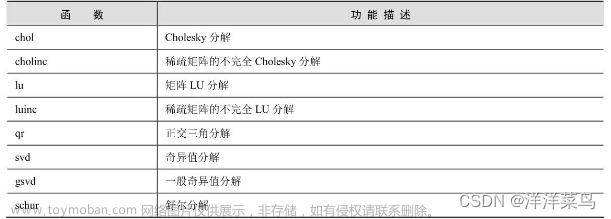
目录 一、对称正定矩阵的Cholesky分解 二、一般方阵的高斯消去法分解 三、矩形矩阵的正交分解 四、舒尔分解 矩阵分解 是把一个矩阵分解成几个“较简单”的矩阵连乘的形式。在MATLAB中矩阵分解的相关函数有: 在MATLAB中, 线性方程组的求解 主要基于4种基本的矩阵分解,即
-
机器学习实战:Python基于SVD奇异值分解进行矩阵分解(八)
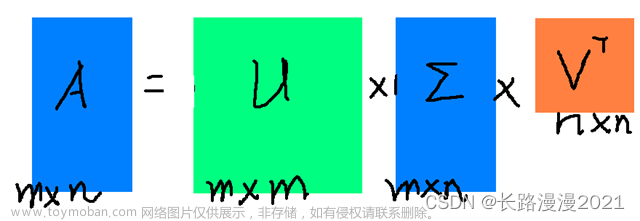
1.1 奇异值分解 奇异值分解( Singular Value Decomposition,SVD )是一种重要的矩阵分解技术,它可以将一个矩阵分解为三个矩阵的乘积,分别为左奇异矩阵、奇异值矩阵和右奇异矩阵。SVD 的原理可以描述如下: 对于任意 m × n m times n m × n 的矩阵 A A A ,它的 SVD 分解为: A = U $
-
矩阵理论| 基础:线性子空间(非平凡子空间)、空间分解、直和分解
前置:线性代数学习笔记3-5:秩1矩阵和矩阵作为“向量”构成的空间 空间 V mathbf V V 有子空间 V 1 mathbf V_1 V 1 (一组基为 α 1 , α 2 , . . . , α k alpha_1,alpha_2,...,alpha_k α 1 , α 2 , ... , α k )和子空间 V 2 mathbf V_2 V 2 (一组基为 β 1 , β 2 , . . . , β l beta_1,beta_2,
-
对称矩阵的三对角分解(Lanzos分解算法)-MINRES算法预热
这篇博客看完以后接着看下一篇博客添加链接描述专门介绍MINRES算法实现就容易了 首先介绍Lanczos分解,Lanzos把对称矩阵转换为一个三对角对称矩阵。考虑三对角对称矩阵如下,考虑正交分解 T = Q T A Q T = Q^T A Q T = Q T A Q T = ( α 1 β 1 0 ⋯ 0 0 β 1 α 2 β 2 0 ⋯ 0 0 β 2 α 3 β 3 ⋯ 0
-
矩阵篇(五)-- 特征值分解(EVD)和奇异值分解(SVD)
设 A n × n A_{n times n} A n × n 有 n n n 个线性无关的特征向量 x 1 , … , x n boldsymbol{x}_{1}, ldots, boldsymbol{x}_{n} x 1 , … , x n ,对应特征值分别为 λ 1 , … , λ n lambda_{1}, ldots, lambda_{n} λ 1 , … , λ n A [ x 1 ⋯ x n ] = [ λ 1 x 1 ⋯ λ n x n ] Aleft[begin{array}{lll
-
【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数
单纯矩阵 :A可对角化⇔①A可对角化;⇔②n个线性无关的特征向量; ⇔③每个特征值的几何重复度等于代数重复度;⇔④特征值λi对应的pi = n - rank(λiE - A)。 等价矩阵 :A(λ)等价于B(λ)⇔① 任意k阶行列式因子相同Dk(λ);⇔②有相同的不变因子dk(λ);⇔③相同的初等因子,且
-
运用谱分解定理反求实对称矩阵
设三阶 实对称矩阵 A A A ,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 lambda_1,lambda_2,lambda_3 λ 1 , λ 2 , λ 3 ,对应的 单位化 特征向量分别为 α 1 , α 2 , α 3 alpha_1,alpha_2,alpha_3 α 1 , α 2 , α 3 且 两两正交 ,则 A = λ 1 α 1 α 1 T + λ 2 α 2 α 2 T + λ 3 α 3 α 3 T A = lam
-
第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解
玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记,例见原文 已知: A r ∼ F A^r sim F A r ∼ F ,求可逆阵 P P P ,使 P A = F PA = F P A = F ( F F F 为 A A A 的行最简形) 方法:利用初等行变换,将矩阵A左边所乘初等矩阵相乘,从而得到可逆矩阵P. 步骤: (1)对矩阵A进行l次初等
-
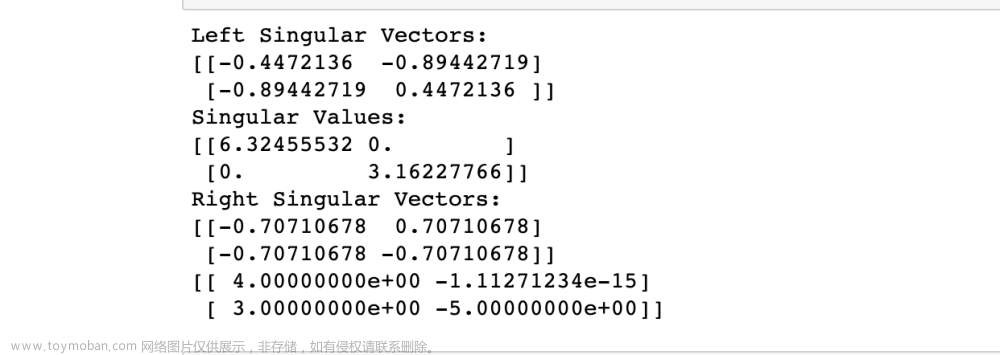
Python实现矩阵奇异值分解(SVD)
Python实现矩阵奇异值分解(SVD) 矩阵奇异值分解(Singular Value Decomposition, SVD)是一种重要的矩阵分解方法,可以将一个矩阵分解成三个矩阵的乘积,即 A = U Σ V T A=USigma V^{T} A = U Σ
-
【国科大——矩阵分析与应用】LU分解
LU分解是旨在将某个矩阵表示为两个或多个矩阵的乘积。 LU分解是将矩阵表示为 A A A = L L L U U U ,其中 L L L 矩阵 代表 Lower Triangular(下三角矩阵) , U U U 矩阵 代表 Upper Triangular(上三角矩阵) 。形象一点就相当于写为 A = ◣ ∗ ◥ A=◣*◥ A = ◣ ∗ ◥ 。 1. 求解U矩阵 先求U矩
-
高等代数复习:矩阵的满秩分解
本篇文章适合个人复习翻阅,不建议新手入门使用 定义:矩阵的左逆、右逆 设 A A A 是 m × n mtimes n m × n 矩阵 若 r ( A ) = n r(A)=n r ( A ) = n ,即 A A A 列满秩,则存在秩为 n n n 的 n × m ntimes m n × m 行满秩矩阵 B B B ,使得 B A = I n BA=I_n B A = I n ,矩阵 B B B 称为 A A A 的左逆 若
-
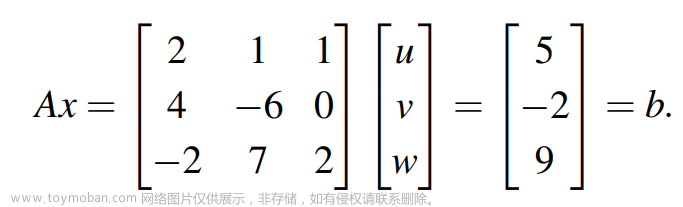
详解矩阵的三角分解A=LU
目录 一. 求解Ax=b 二. 上三角矩阵分解 三. 下三角矩阵分解 四. 矩阵的三角分解 举例1:矩阵三角分解 举例2:三角分解的限制 举例3:主元和乘法因子均为1 举例4:U为单位阵 小结 我们知道高斯消元法可以对应矩阵的基础变换。先来看我们比较熟悉的Ax=b模型,如下: 解这个方
-
最优化方法(三)——矩阵QR分解
1.熟练掌握 QR 分解 Gram–Schmidt方法; 2.掌握 Householder 方 法 ; 3. 能够判断 矩阵是否可逆 ,并 求出其逆矩阵 。 读取附件 MatrixA.mat 文件中的 矩阵 A , 利用 Gram–Schmidt(GS) 算法对A进行QR分解 。 (1) 验证GS是否 能稳定 进行QR分解矩阵A ,其 Q矩阵 是否正交? (2) 实现 Householder
-
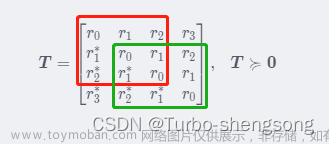
半正定Toeplitz矩阵的范德蒙德分解
Toeplitz矩阵 的 定义 :Matrices whose entries are constant along each diagonal are called Toeplitz matrices . 形如 T = [ r 0 r 1 r 2 r 3 r − 1 r 0 r 1 r 2 r − 2 r − 1 r 0 r 1 r − 3 r − 2 r − 1 r 0 ] (1) boldsymbol{T}=left[ begin{matrix} r_0 r_1 r_2 r_3\\\\ r_{-1} r_0 r_1 r_2\\\\ r_{-2} r_{-1} r_0 r_1\\\\ r_{-3} r_{-2} r_{-1} r_0\\\\ end{matri
-
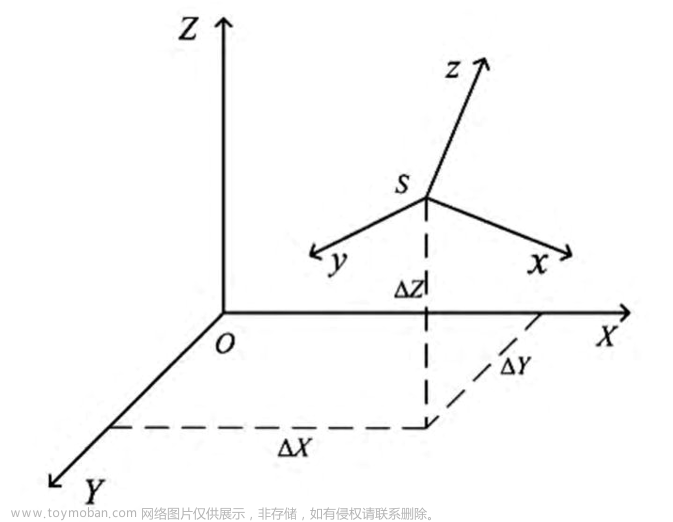
基于opencv的SVD分解求解变换矩阵
在机器视觉领域,坐标系之间的转换是必不可少的。空间坐标转换的实质是用公共点的两套坐标去推导出两个坐标系之间的转换关系:R(旋转矩阵)和T(平移向量)。 其实点云的配准过程就是求解旋转矩阵R和平移向量T,这里记目标函数为: 式中,n是匹配点个数,假设其最
-
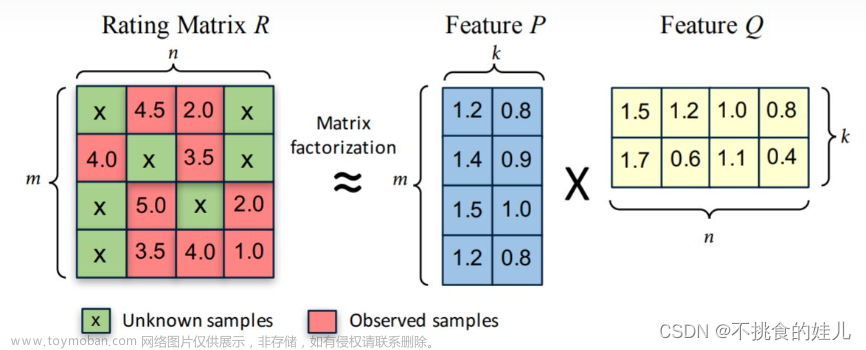
矩阵分解(Matrix-Factorization)无门槛
本章主要介绍矩阵分解常用的三种方法,分别为: 1 ◯ textcircled{1} 1 ◯ 特征值分解 2 ◯ textcircled{2} 2 ◯ 奇异值分解 3 ◯ textcircled{3} 3 ◯ Funk-SVD 矩阵分解原理: textbf{large 矩阵分解原理:} 矩阵分解原理: 矩阵分解算法将 m × n mtimes n m × n 维的矩阵 R R R 分解为 m ×