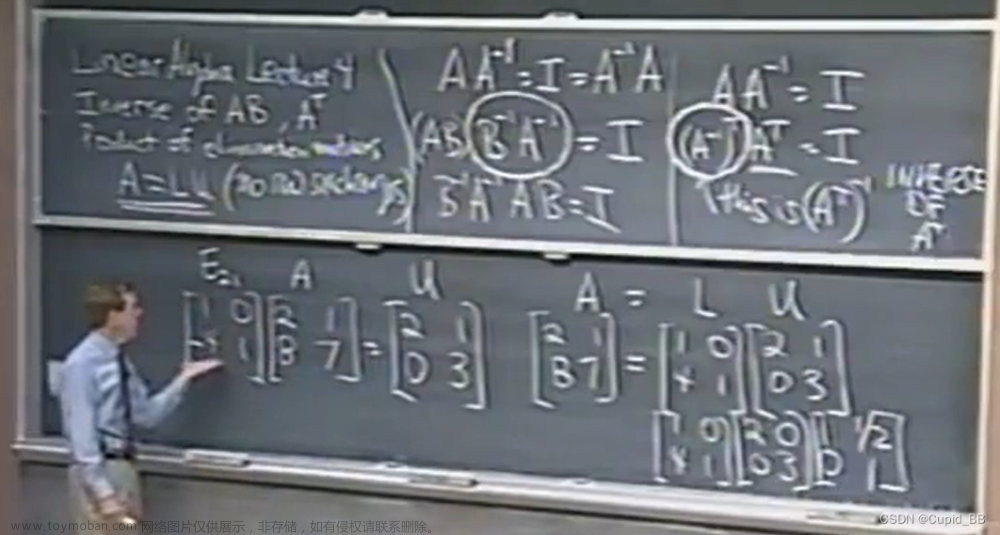低秩矩阵分解
-
【Python】NMF非负矩阵分解算法(测试代码)
欢迎关注 『Python』 系列,持续更新中 欢迎关注 『Python』 系列,持续更新中 从多元统计的观点看,NMF是在非负性的限制下,在尽可能保持信息不变的情况下,将高维的随机模式简化为低维的随机模式H,而这种简化的基础是估计出数据中的本质结构W;从代数的观点看,NMF是
-
【高等工程数学】南理工研究生课程 突击笔记5 矩阵分解与广义逆矩阵
第三章主要内容如下 提示:以下是本篇文章正文内容,下面案例可供参考 矩阵分解是将矩阵分解成两个或三个在形式上、性质上比较简单的矩阵的乘积。 操作方式见例题3.1 将A的第一行元素照抄 再算 第一列的元素Ln1 求第二阶的行元素 求第二阶的列元素 求三阶对角线元素
-
本质矩阵(Essential Matrix)E进行分解的过程
分解本质矩阵的过程遵循以下步骤: 使用奇异值分解(SVD)计算本质矩阵E的分解。SVD分解是一种将矩阵分解为三个矩阵的乘积的方法,它的形式为 E = UΣV^T,其中U和V是正交矩阵,Σ是对角矩阵。此步骤的结果存储在u、w和vt中。 把U矩阵的第三列复制到t,并进行归一化。t代表
-
线性代数笔记4--矩阵A的LU分解
1. 矩阵的转置 1.1 定义 矩阵的转置,即矩阵的行列进行互换。 A = [ 1 2 3 4 5 6 ] A= begin{bmatrix} 1 2 3 \\\\ 4 5 6\\\\ end{bmatrix} A = [ 1 4 2 5 3 6 ] 矩阵 A A A 的转置 B = A ⊤ = [ 1 4 2 5 3 6 ] B=A^top= begin{bmatrix} 1 4\\\\ 2 5\\\\ 3 6 end{bmatrix} B = A ⊤ = 1 2 3 4 5 6 1.2 性质 ( A ⊤ ) ⊤ = A
-
【数学与算法】奇异矩阵、奇异值、奇异值分解、奇异性
我们经常会碰到几个名词很相近的一些数学术语,例如 奇异矩阵、奇异值、奇异值分解、奇异性 ,经常会混淆,这里把它们的定义放在一起,做一下总结: 1.奇异矩阵: 奇异矩阵 是线性代数的概念,就是该矩阵的 秩不是满秩 。 首先,看这个矩阵是不是方阵,即行数和列数
-
【Python】scipy稀疏矩阵的奇异值分解svds
当 A A A 是方阵时,可以很容易地进行特征分解: A = W Σ W − 1 A=WSigma W^{-1} A = W Σ W − 1 ,其中 Σ Sigma Σ 是 A A A 的特征值组成的对角矩阵。如果 W W W 由标准正交基组成,则 W − 1 = W T W^{-1}=W^T W − 1 = W T ,特征分解可进一步写成 W T Σ W W^TSigma W W T Σ W 。 然而,当 A A A 不是方
-
线性代数 --- 矩阵的QR分解,A=QR
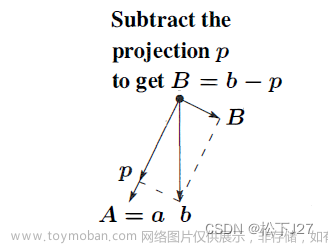
首先先简单的回顾一下Gram-Schmidt正交化过程的核心思想。即,如何把一组线性无关的向量构造成一组标准正交向量,或者说,如何把一般的线性无关矩阵A变成标准正交矩阵Q。 给定一组线性无关的向量a,b,c,我们希望构造出一组相互垂直的单位向量q1,q2,q3。
-
SLAM ORB-SLAM2(22)分解基础矩阵
在 《SLAM ORB-SLAM2(12)估算运动并初始地图点》 中了解到 估算两帧间相对运动过程: 记录特征点对的匹配关系 RANSAC 采样准备 计算H矩阵或者F矩阵 判断并选取模型求位姿过程 在
-
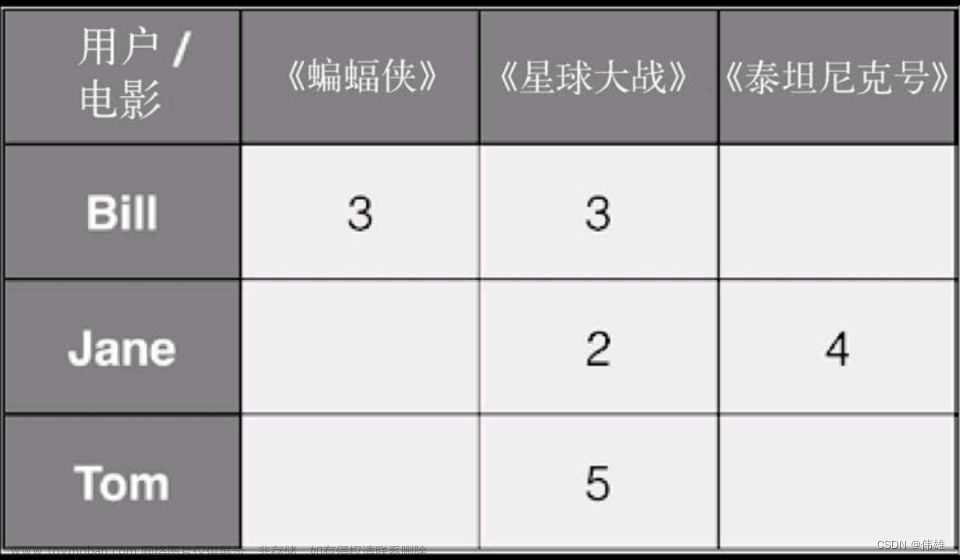
【推荐系统入门到项目实战】(三):矩阵分解和ALS算法
🌸个人主页:JOJO数据科学 📝个人介绍: 统计学top3 高校统计学硕士在读 💌如果文章对你有帮助,欢迎✌ 关注 、👍 点赞 、✌ 收藏 、👍 订阅 专栏 ✨本文收录于【推荐系统入门到项目实战】 本系列主要分享一些学习推荐系统领域的方法和代码实现。 之前我们介绍了推荐
-
推荐系统 | 基础推荐模型 | 矩阵分解模型 | 隐语义模型 | PyTorch实现
基础推荐模型——传送门 : 推荐系统 | 基础推荐模型 | 协同过滤 | UserCF与ItemCF的Python实现及优化 推荐系统 | 基础推荐模型 | 矩阵分解模型 | 隐语义模型 | PyTorch实现 推荐系统 | 基础推荐模型 | 逻辑回归模型 | LS-PLM | PyTorch实现 推荐系统 | 基础推荐模型 | 特征交叉 | FM | FFM |
-
MIT - 线性代数-LU_LDU分解|单位矩阵
U为消元结果(行变换),L为行变换矩阵的逆矩阵 D为主元(Pivot)A的主对角线元素,在这里为2、3,U为对D做列变换使其得到LU中的U 为什么要写成A=LU而不是E21A=U呢?因为A=LU中L只包含行变换信息,E21A=U还有额外的数字 2×2 2 3×3 3×2=6 4×4 4×3×2=24 结论:单位矩阵的逆=转置矩阵(
-
C语言——利用矩阵LU分解法求逆、行列式
本章介绍了LU分解法,以及如何利用LU分解法求逆、行列式,针对每个公式、原理、代码进行了详细介绍,希望可以给大家带来帮助。 LU分解法与高斯法求逆一样,可以进行较高维数的矩阵运算(可计算万维及以上,但是精度不能保证,并且占有内存大,高维矩阵需要进行分块
-
线性代数 --- LU分解(Gauss消元法的矩阵表示)
首先, LU分解实际上就是用矩阵的形式来记录的高斯消元的过程 。其中,对矩阵A进行高斯消元后的结果为矩阵U,是LU分解后的两个三角矩阵中其中之一。U是一个上三角矩阵,U就是上三角矩阵upper triangle的首字母的大写。 高斯消元的每一步都
-
LightFM:一款开源推荐系统框架,可以轻松实现大规模矩阵分解,快速、高效地处理大型矩阵
作者:禅与计算机程序设计艺术 LightFM 是由 Yelp 开发的一款开源推荐系统框架,可以轻松实现大规模矩阵分解。该项目基于 TensorFlow 和 Keras 框架,可以快速、高效地处理大型矩阵。它具有以下特点: 提供了一种简单的方法来训练矩阵分解模型,即通过定义项间的交互矩阵和用
-
矩阵:采用奇异值分解(SVD)对n个点进行平面拟合
奇异值分解(Singular Value Decomposition, SVD),是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。奇异值分解在某些方面与对称矩阵或厄米矩阵基于特征向量的对角化类似。对称矩阵特征向量分解的基础是谱分析,而奇异值分解则是谱分析理论在任意矩
-
特征值与特征向量: 矩阵的奇异值分解与主成分分析
随着数据量的增加,数据处理和分析变得越来越复杂。在大数据领域,我们需要一种有效的方法来处理高维数据,以便更好地理解数据之间的关系和模式。这就是奇异值分解(Singular Value Decomposition, SVD)和主成分分析(Principal Component Analysis, PCA)发挥作用的地方。在本文中,我们将
-
【线性代数/机器学习】矩阵的奇异值与奇异值分解(SVD)
我们知道,对于一个 n × n ntimes n n × n 的矩阵 A A A ,如果 A A A 有 n n n 个线性无关的特征向量,则 A A A 可以相似对角化,即存在可逆矩阵 P P P 使得 A = P Λ P − 1 A=PLambda P^{-1} A = P Λ P − 1 ,其中 Λ Lambda Λ 是 A A A 的特征值组成的对角阵。 P P P 的列实际上就是 A A A 的特征向
-
理解非负矩阵和张量分解:快速算法的Matlab实现与优化实践
第一部分:非负矩阵分解(Non-negative Matrix Factorization,NMF)的基本原理 非负矩阵分解(NMF)是一种广泛应用的线性代数技术,特别适用于大规模的数据集分析。其基本思想是将一个非负矩阵分解为两个低秩的非负矩阵的乘积,使得矩阵的内在结构得以暴露并利于进一步分析。
-
大数据课程K18——Spark的ALS算法与显式矩阵分解
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ⚪ 掌握Spark的ALS算法与显式矩阵分解; ⚪ 掌握Spark的ALS算法原理; 我们在实现推荐系统时,当要处理的那些数据是由用户所提供的自身的偏好数据,这些数据被称作显式偏好数据,由显示偏好数据建立的矩阵称
-
04 MIT线性代数-矩阵的LU分解 Factorization into A=LU
目的: 从矩阵的角度理解高斯消元法, 完成 LU 分解得到 A = LU U 为上三角阵(Upper triangular matrix), L 为下三角阵(Lower triangular matrix), 通过分解得到对角阵 D (diagonal matrix) 设定一组消元矩阵,其中 E31 为单位阵 I ,其它两个消元矩阵如下: row3 -5 newrow2 = row3 -5( row2 -2 row1 )= row3 -