低秩矩阵 稀疏分解视频
-
用三元组表实现稀疏矩阵的基本操作
目录 问题描述 数据结构 算法设计 算法流程图 源代码 运行结果 编写程序用三元组表实现稀疏矩阵的按列转置操作。 本设计使用三元组表实现。 程序中设计了三个函数: 1.函数InitSPNode()用来建立一个稀疏矩阵的三元组表。 首先输入行数、列数和非零元的
-
【数据结构】数组和字符串(四):特殊矩阵的压缩存储:稀疏矩阵——三元组表
【数据结构】数组和字符串(一):矩阵的数组表示 矩阵是以按行优先次序将所有矩阵元素存放在一个一维数组中。但是对于特殊矩阵,如对称矩阵、三角矩阵、对角矩阵和稀疏矩阵等, 如果用这种方式存储,会出现大量存储空间存放重复信息或零元素的情况,这样会造
-
numpy 邻接矩阵转稀疏矩阵 array to scipy csr_matrix
也就是说,一个dense的numpy矩阵,如何转换成scipy包里面的sparse的csr矩阵看代码: 输出: print(csr_a.toarray()) print(csr_a.tocoo())
-
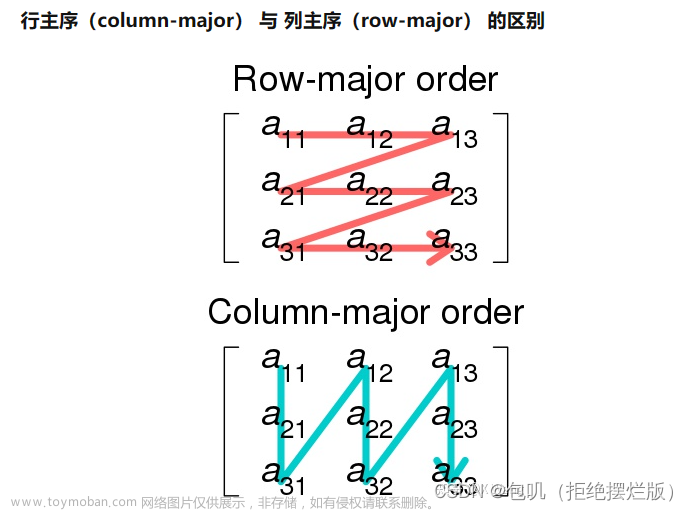
数据结构 | 第七章:数组和矩阵 | 行主映射和列主映射 | 稀疏矩阵
7.1.1 抽象数据类型 7.1.2 C++数组的索引 K维数组的索引(或下标) [ i 1 ] [ i 2 ] [ i 3 ] . . . [ i k ] [i_1][i_2][i_3]...[i_k] [ i 1 ] [ i 2 ] [ i 3 ] ... [ i k ] k维数组创建: int score [ u 1 ] [ u 2 ] [ u 3 ] . . . [ u k ] [u_1][u_2][u_3]...[u_k] [ u 1 ] [ u 2 ] [ u 3 ] ... [ u k ] ( u i u_i u i
-
矩阵的谱分解 (详细推导步骤~~~特征值分解特征向量
所谓矩阵的分解,就是将一个矩阵写成结构比较简单的或性质比较熟悉的另一些矩阵的乘积。矩阵的分解方法有很多种,包括三角分解、QR(正交三角)分解、最大秩分解、奇异值分解和谱分解,所有这些分解在数值代数和最优化问题的解法中都扮演着十分重要的角
-
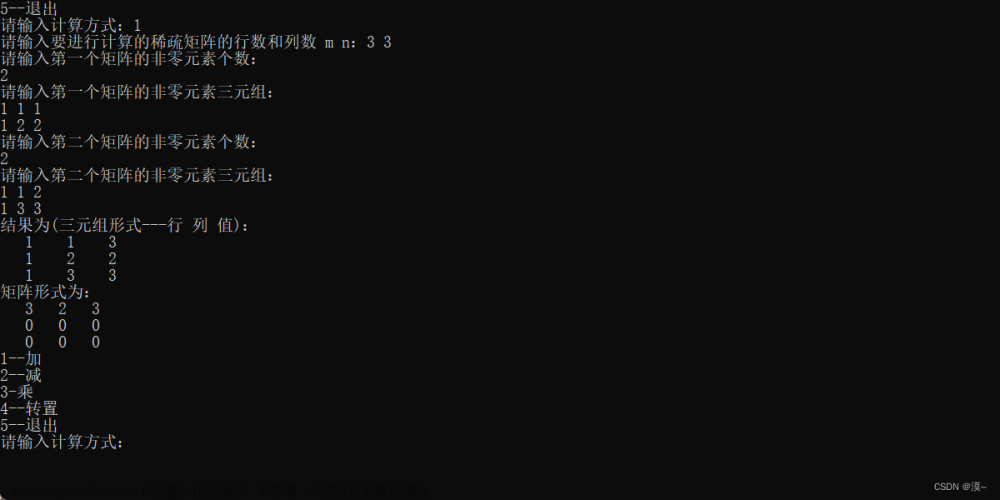
稀疏矩阵的运算-加、减、乘、转置(C-数据结构)
以三元组的形式给出输入数据,选择对应的运算后给出对应输出结果(稀疏矩阵的运算器) 页面布局就不说了,这里大概说一下各个运算模块的实现 加减法 将三元组中对应的元素行列位置进行比较,将较为靠前的元素直接放进新的三元组存储结构,位置相同的元素通过对应符
-
ML@python@稀疏矩阵的存储和表示@CSR格式
Sparse matrix - Wikipedia CSR是Compressed Sparse Row的缩写,是一种稀疏矩阵的压缩存储格式。稀疏矩阵是指其中大部分元素为0的矩阵。在机器学习中,由于特征维度通常很高,因此特征矩阵往往是稀疏矩阵。使用CSR格式可以节省存储空间并加快矩阵运算的速度。 在CSR格式中,矩阵被视
-
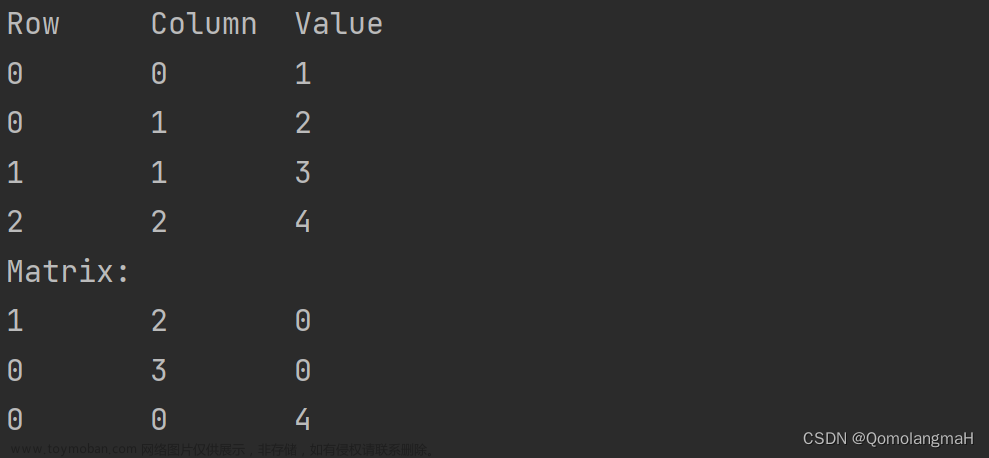
PTA:三元组顺序表表示的稀疏矩阵转置Ⅱ
三元组顺序表表示的稀疏矩阵转置Ⅱ。设a和b为三元组顺序表变量,分别表示矩阵M和T。要求按照a中三元组的次序进行转置,并将转置后的三元组置入b中恰当的位置。 输入第1行为矩阵行数m、列数n及非零元素个数t。 按行优先顺序依次输入t行,每行3个数,分别表示非零元素
-
【华为OD机试】矩阵稀疏扫描【2023 B卷|100分】
【 华为OD机试】-真题 !!点这里!! 【 华为OD机试】真题考点分类 !!点这里 !! 题目描述 如果矩阵中的许多系数都为零,那么该矩阵就是稀疏的。 对稀疏现象有兴趣是因为它的开发可以带来巨大的计算节省, 并且在许多大的实践中都会出现矩阵稀疏的问题。 给定一个矩阵,
-
华为OD机试 - 矩阵稀疏扫描(Java & JS & Python)
题目描述 如果矩阵中的许多系数都为零,那么该矩阵就是稀疏的。对稀疏现象有兴趣是因为它的开发可以带来巨大的计算节省,并且在许多大的实践中都会出现矩阵稀疏的问题。 给定一个矩阵,现在需要逐行和逐列地扫描矩阵,如果某一行或者某一列内,存在连续出现的0的
-
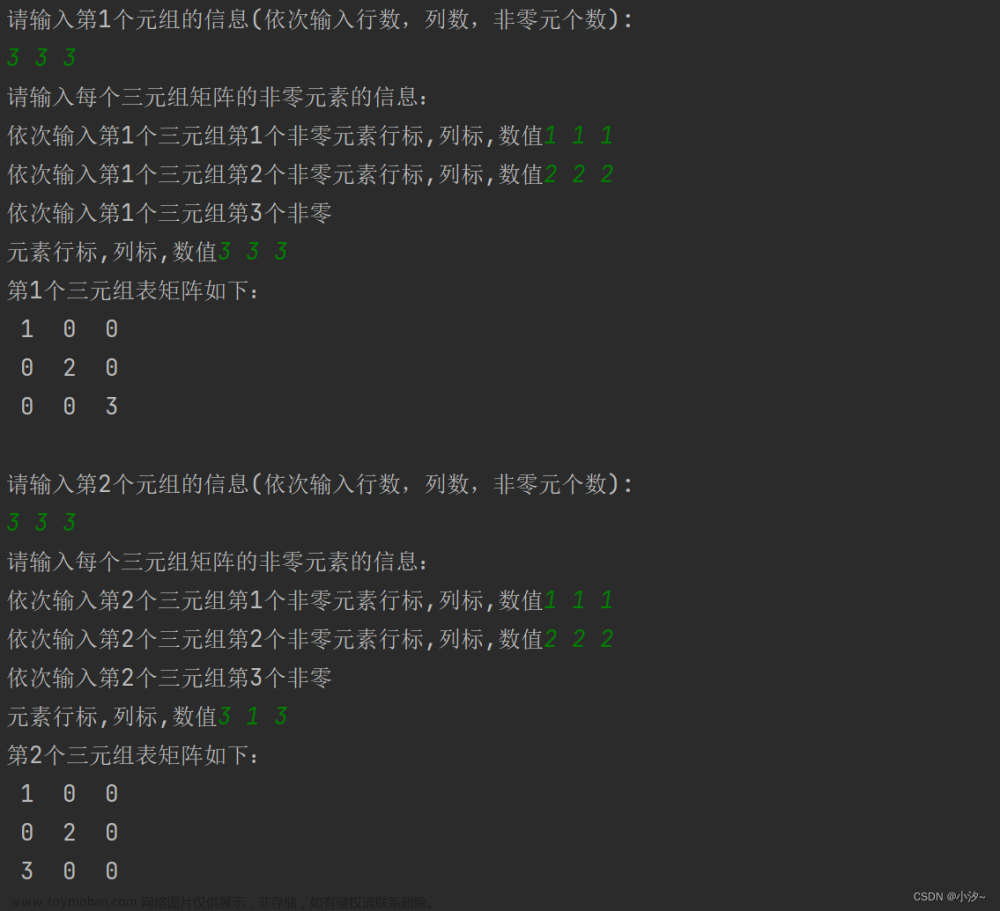
【C 数据结构】以三元组表形式表示稀疏矩阵,实现两个矩阵的加法、减法
目的:以三元组表形式表示稀疏矩阵,实现两个矩阵的加法、减法。 实验步骤 1. 定义三元组存储结构 2. 输入稀疏矩阵:首先应输入矩阵的行数、列数和非零项的数目,并判别给出的两个矩阵的行、列数对于所要求进行的运算是否匹配。可设矩阵的行数和列数均不超过20。接
-
4.矩阵的分解
怎么计算矩阵又快又准——矩阵的分解 先判断Doolittle分解是否唯一,再进行Doolittle分解 各阶顺序主子式均不为0,Doolittle分解唯一; 特殊的:正定/负定矩阵,Doolittle分解唯一;严格行(列)对角占优矩阵,Doolittle分解唯一; Doolittle分解的算法 一共 5 种分解 【定义】Doolittle分解
-
矩阵的分解
怎么计算矩阵又快又准——矩阵的分解 先判断Doolittle分解是否唯一,再进行Doolittle分解 各阶顺序主子式均不为0,Doolittle分解唯一; 特殊的:正定/负定矩阵,Doolittle分解唯一;严格行(列)对角占优矩阵,Doolittle分解唯一; Doolittle分解的算法 一共 5 种分解 【定义】Doolittle分解
-
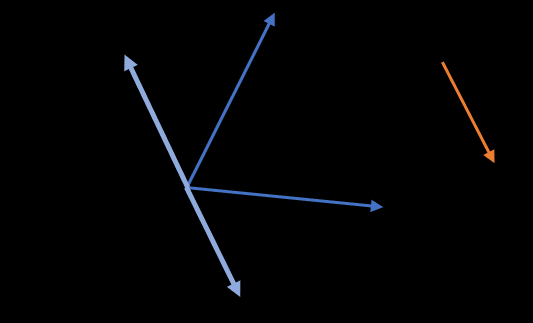
矩阵分析:特征值分解
伸缩 一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵: 因为这个矩阵M乘以一个向量(x,y)的结果是: 旋转 除了伸缩变换,也可以进行旋转变换。 上面的矩阵是对称的,所以这个变
-
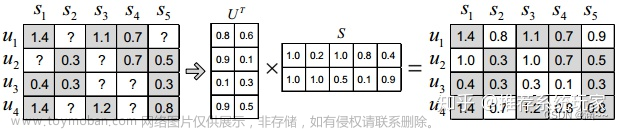
矩阵分解算法
目录 一·、定义(什么是矩阵分解) 二、矩阵分解的原理 三、矩阵分解的方法 四、矩阵分解的步骤 五、代码实现 六、矩阵分解的优缺点 矩阵分解就是预测出评分矩阵中的缺失值,然后根据预测值以某种方式向用户推荐。常见的矩阵分解方法有基本矩阵分解(basic MF),正
-
矩阵分解及其Eigen实现
主要是用来记录自己的学习过程,内容也主要来自于网上的各种资料,然后自己总结而来,参考的资料都以注明,感谢这些作者的分享。如果内容有误,请大家指点。 定义 将矩阵等价为两个矩阵 L L L 和 U U U 的乘积 ,其中 L L L 和 U U U 分别是单位下三角矩阵和上三角
-
矩阵分析:QR分解
Householder变换是一种简洁而有意思的线性变换,也可称为镜面反射变换,Householder变换矩阵为 H = I − w T w H=I-w^Tw H = I − w T w 考虑向量 α alpha α 和一个单位向量 w : w T w = 1 w:w^{T}w=1 w : w T w = 1 α alpha α 在 w w w 方向上的分量是 α w / / = ( w T α ) w = w w T α alpha _{w_{//}}=left( w^{T}
-
矩阵的奇异值分解
注:本博文为本人阅读论文、文章后的原创笔记,未经授权不允许任何转载或商用行为,否则一经发现本人保留追责权利。有问题可留言联系,欢迎指摘批评,共同进步!!! 假设矩阵 A mathbf{A} A 是一个 M × N M times N M × N 大小的矩阵。对其进行奇异值分解后可以得到: A
-
Python矩阵LU分解
scipy.linalg 中提供了一系列矩阵分解函数,其中最基础的肯定是LU分解。 LU分解,即使得矩阵 A A A 分解为 L U LU LU ,其中 L L L 为下三角阵, U U U 为上三角阵。对于这两种矩阵, scipy.linalg 中提供了 tril, triu ,可以将第 k k k 条对角线下面或上面的所有元素置零,即可以此获取L矩
-
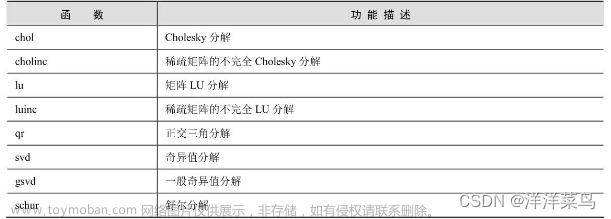
11、矩阵的分解
目录 一、对称正定矩阵的Cholesky分解 二、一般方阵的高斯消去法分解 三、矩形矩阵的正交分解 四、舒尔分解 矩阵分解 是把一个矩阵分解成几个“较简单”的矩阵连乘的形式。在MATLAB中矩阵分解的相关函数有: 在MATLAB中, 线性方程组的求解 主要基于4种基本的矩阵分解,即