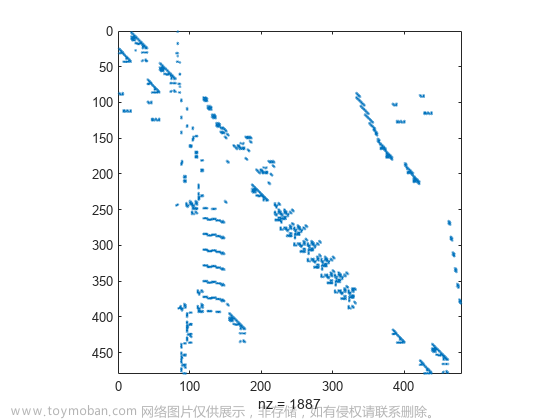
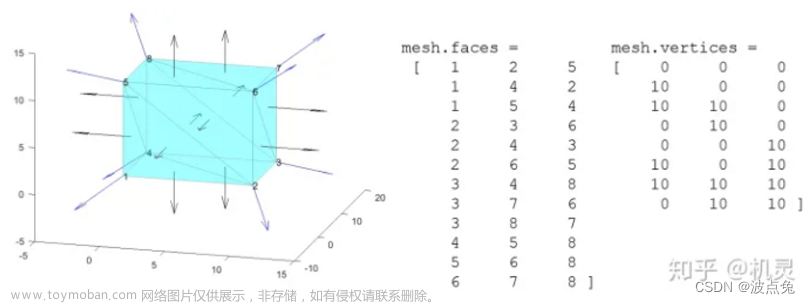
低秩矩阵 稀疏分解过程
-
【scipy 基础】--稀疏矩阵
稀疏矩阵 是一种特殊的矩阵,其非零元素数目远远少于零元素数目,并且非零元素分布没有规律。 这种矩阵在实际应用中经常出现,例如在物理学、图形学和网络通信等领域。 稀疏矩阵 其实也可以和一般的矩阵一样处理,之所以要把它区分开来进行特殊处理,是因为: 一
-
[Eigen中文文档] 稀疏矩阵操作
文档总目录 英文原文(Sparse matrix manipulations) 处理和解决稀疏问题涉及各种模块,总结如下: 模块 头文件 内容 SparseCore #includeEigen/SparseCore SparseMatrix和SparseVector类、矩阵集合、基本稀疏线性代数(包括稀疏三角求解器) SparseCholesky #includeEigen/SparseCholesky 直接稀疏LLT和LDLT Chole
-
稀疏矩阵的表示以及转置
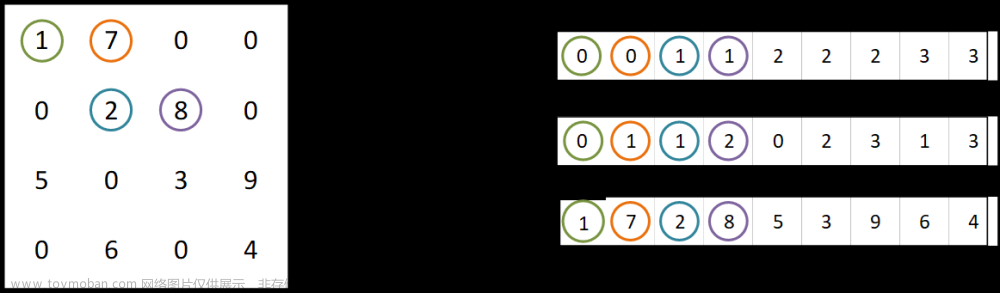
目录 1.稀疏矩阵概念 2.三元组表 3.稀疏矩阵的转置 4.题目实现 矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵。 图示: 在存储稀疏矩阵时,为了节省存储单元,很自然地想到使用压缩存储方法。但由于非零元
-
【数据结构】稀疏矩阵存储的三种方法及三元组表示稀疏矩阵转置算法的两种实现 —— C++
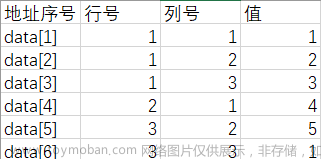
1. 三元组顺序表数据结构 注意:data[]中的元素是按行存储或者按列存储的,所以 在将三元组逆置时,不能简单地将行列下标对换,data[]数组中元素的顺序也需要重新排列 2. 三元组表示稀疏矩阵转置算法1 3. 三元组表示稀疏矩阵转置算法2:快速转置 为了 便于随机存取任意一
-
稀疏矩阵的加法和乘法(三元组)
三元组方法: 主要的特点就是最后的结果矩阵均由三元组的形式来表达,调用函数再以矩阵形式输出 (1)稀疏矩阵加法 (下图参考懒猫老师《数据结构》课程相关笔记) 这里与普通矩阵加法不同的是,稀疏矩阵的三元组在加法计算时, 如果两个矩阵中的元素相加不为0时
-
稀疏矩阵的三元组表示----(算法详解)
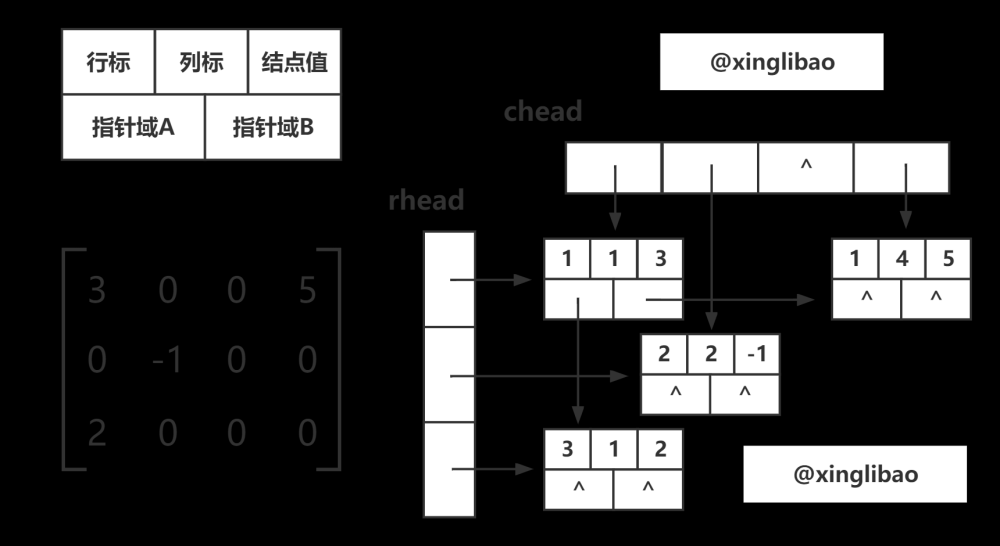
目录 基本算法包括:(解释都在代码里) 1.创建 2.对三元组元素赋值 3.将三元组元素赋值给变量 4.输出三元组 5.转置(附加的有兴趣可以看看) 稀疏矩阵的概念:矩阵的非零元素相较零元素非常小时,这个矩阵就叫稀疏矩阵。 稀疏矩阵可以用 三元组表示 和 十字链表表示
-
数据结构-拓展突破-特殊矩阵(对称矩阵,三角矩阵,三对角矩阵,稀疏矩阵)的压缩存储)
对称矩阵的定义: 若n阶方阵中任意一个元素a,都有a(i,j)=a(j,i)则该矩阵为对称矩阵 也就是说对称矩阵的元素关于对角线对称。对角线上半部分称为上三角区,下半部分称为下三角区。 对称矩阵的压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区) 可以定义一维数
-
MKL稀疏矩阵运算示例及函数封装
Intel MKL库提供了大量优化程度高、效率快的稀疏矩阵算法,使用MKL库的将大型矩阵进行稀疏表示后,利用稀疏矩阵运算可大量节省计算时间和空间,但由于MKL中的原生API接口繁杂,因此将常用函数封装,便于后续使用,最后在实际例子中调用接口执行想要的矩阵运算。 稀疏矩
-
三元组操作(相加)——稀疏矩阵(c语言)
运行环境:TDM-GCC 三元组用来存储 稀疏矩阵 比较节省空间,因为稀疏矩阵大部分都是零元素,而三元组只记录非零元素。 这里两个相加的矩阵有着同样的 i行 j列。 运行结果: 行数:3 列数:4 元素个数:4 -------------------- 第0 行 第1 列 1
-
稀疏矩阵转置算法(C语言)
(参考数据结构教材,严蔚敏,吴伟民版 p99,多谢阅读,望对您有帮助) 无论是几维的数组,在计算机中都是 以一维数组 的方式进行存储的。 矩阵:相当于 二维数组 ,它的存储,依然是用一维数组的方式进行存储。 nxn的矩阵,在计算机空间上, 需要nxn个空间 。 稀疏矩
-
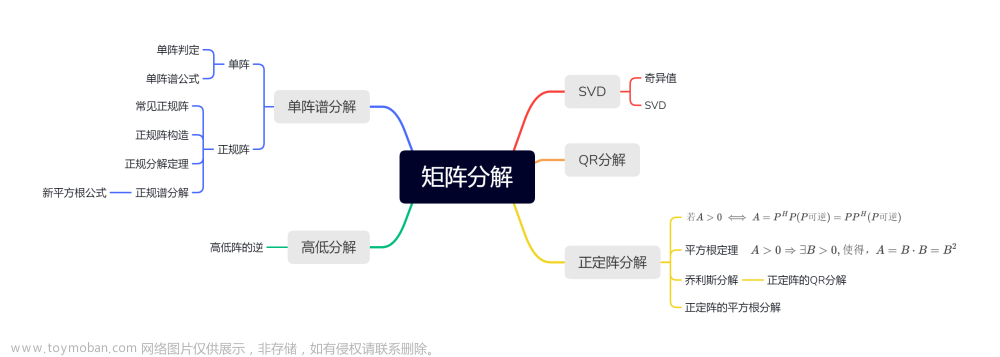
矩阵分析——矩阵分解
矩阵分解指的是将复杂的矩阵分解成比较简单的矩阵的乘积的形式。在数值代数、矩阵论和最优化应用。 三角分解: 矩阵的三角分解:将一个方阵 A pmb{A} A A 分解成一个下三角阵 L pmb{L} L L 和一个上三角矩阵 R pmb{R} R R 的乘积,即 A = L R pmb{A}=pmb{L}pmb{R} A A = L L R R 。 充分必
-
一分钟读懂:矩阵的特征值分解、奇异值分解和伪逆矩阵
通过把矩阵运算分解成多个矩阵的乘法,可以简化矩阵运算,也可发现对应线性变换的一些内在规律和特性。根据不同的目的,有不同的分解策略。本文我们讨论最常用的特征值分解和奇异值分解。 定义了矩阵的加、减、乘、除(逆)运算后,数学家们自然希望探索矩阵更多
-
【矩阵论】2. 矩阵分解——SVD
矩阵论的所有文章,主要内容参考北航赵迪老师的课件 [注]由于矩阵论对计算机比较重要,所以选修了这门课,由于不是专业搞数学的,所以存在很多口语化描述,而且对很多东西理解不是很正确与透彻,欢迎大家指正。我可能间歇性忙,但有空一定会回复修改的。 矩阵论
-
【scipy.sparse包】Python稀疏矩阵详解
数组和矩阵是数值计算的基础元素 。目前为止,我们都是使用NumPy的ndarray数据结构来表示数组,这是一种同构的容器,用于存储数组的所有元素。 有一种特殊情况, 矩阵的大部分元素都为零,这种矩阵被称为稀疏矩阵 。对于稀疏矩阵,将所有零保存在计算机内存中的效率很
-
matlab使用教程(13)—稀疏矩阵创建和使用
使用稀疏矩阵存储包含众多零值元素的数据,可以节省大量内存并加快该数据的处理速度。 sparse 是一种属性,可以将该属性分配给由 double 或 logical 元素组成的任何二维 MATLAB 矩阵。通过 sparse 属性,MATLAB 可以: • 仅存储矩阵中的非零元素及其索引。
-
稀疏矩阵的三元组存储及快速转置
目录 问题描述 完整代码 详细分析 本节文章 【问题描述】 实现稀疏矩阵的三元组表存储和快速转置运算。 【输入形式】 输入一个整型的6阶稀疏矩阵。 【输出形式】 输出稀疏矩阵的三元组表形式,使用快速转置方法进行转置运算,输出辅助数组num和cpot的值及转置后的三
-
【三维点云处理】顶点、面片、邻接矩阵、邻接距离矩阵以及稀疏存储概念
vertices-节点(3是点的三维坐标) Double类型的矩阵。用来存放所有构成mesh的节点,假设该mesh由N个三维节点构成,那么vertices就是一个N*3的矩阵,vertices(i, j) 表示了第i个节点第j维的坐标。 faces-面片(3是构成三角形面片的3个点) Integer类型的矩阵。用来存放节点之间的连接关
-
矩阵分析与计算学习记录-矩阵分解
本章重点内容: 满秩分解:存在性、方法 三角分解:Doolittle分解、两种求解方法、cholesky分解 QR分解:定义、Householder变换、Givens变换、Schmidt正交化方法求QR分解、上Hessenberg矩阵 奇异值分解 下面看个例子,对矩阵进行满秩分解 矩阵的三角分解是最基本的一种矩阵分解
-
Matlab实现矩阵的QR分解和奇异值分解
1.安装并运行matlab软件; 2.在命令窗口行输入需要进行QR分解的矩阵,并输入求秩及进行QR分解的函数,如下图; 3.点击回车键,则可得Q及R矩阵; 4.若要查看之前所输入的矩阵及所获得的相关变量,可从右侧工作区窗口查看; 5.单击需要查看的变量名,则相关变量会被显示在主窗口
-
基于Givens矩阵的QR矩阵分解
QR分解是一种将矩阵分解为正交矩阵和上三角矩阵的方法。在QR分解中,正交矩阵Q的转置是它的逆矩阵,因此QR分解可以用于求解线性方程组、最小二乘问题等。 二阶Givens矩阵 一般地,二阶Givens矩阵记为下列形式: 其中 下面开始介绍基于Givens矩阵的QR分解算法。Givens矩阵是一

![[Eigen中文文档] 稀疏矩阵操作](https://imgs.yssmx.com/Uploads/2024/02/497914-1.jpeg)