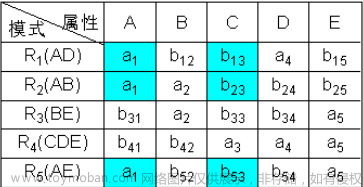
最小函数依赖集的求解方法
-
2308d的静态构造函数循环依赖示例
原文 这里有两个论点:这不能是 CRT 构造器,因为它依赖于 D运行时 ,并且认为它应该进入 自己 的模块是一个 QoL 问题,当你想要 私有 到类而不是 私有 到模块时,可为 类 提供它,因为 语言 按期望工作,而这里不是. 亚当的示例: 因为依赖 D运行时 ,不能是 CRT 构造器,但也不能放进
-
Fluent求解器——空间离散化方法
质量通量的计算方法可以在\\\"Solution Methods\\\"面板中的\\\"Flux Type\\\"下拉框中选择。对于压力基求解器,可以从以下选项中进行选择: (1) Rhie-Chow: distance based 。此通量选项应用距离加权高阶速度插值,并针对压力梯度差进行 Rhie-Chow 校正。这是默认选项,建议用于大多数情况
-
vscode代码函数依赖跳转怎么做
在 Visual Studio Code 中,您可以使用快捷键 F12 来跳转到代码函数的定义处。也可以使用快捷键 Ctrl+Click 或者在函数名上按下 Alt+Click 来跳转到函数定义处。 此外,您还可以使用 Visual Studio Code 的“Peek Definition”功能来查看函数定义,而不必离开当前文件。要使用此功能,请在函
-
如何用随机方法求解组合优化问题(五)
这是一篇笔记,是对于B站up主马少平的视频(第四篇 如何用随机方法求解组合优化问题(五))的学习与记录。 【回顾】:局部最优问题 在局部搜索问题中,可能会陷入局部最优解(如上图中的B、C),解决思路是: 以概率接受差解 。 【回顾】:退火过程中 从状态 (i)
-
如何用随机方法求解组合优化问题(六)
这是一篇笔记,是对于B站up主马少平的视频(第四篇 如何用随机方法求解组合优化问题(六))的学习与记录。 算法实现需要确定的参数: 初始温度 (t_0) ; 温度 (t) 的衰减函数,即温度的下降方法; 算法的终止准则,终止温度 (t_f) 或者终止条件; 每个温度 (t) 下的
-
如何用随机方法求解组合优化问题(二)
组合问题由于其可能的解的数量十分庞大,无法用穷举法求解最优解。 局部搜索算法旨在减少复杂度的情况下寻找最优解,尽管其不一定能够找到全局最优解,但是往往可以找到满意的局部最优解。 类似于盲人爬山,无法看到全局的景象,但是有拐杖可以探测临近的区域。
-
如何用随机方法求解组合优化问题(四)
这是一篇笔记,是对于B站up主马少平的视频(第四篇 如何用随机方法求解组合优化问题(四))的学习与记录。 这篇笔记还没有介绍到模拟退火算法,而是记录退火这一物理过程以及相关的公式。 最主要的内容是如何将退火过程的特点迁移到后续的算法设计中。 退火是固体
-
如何用随机方法求解组合优化问题(三)
皇后问题 : 在一个 (ntimes n) 的棋盘上,每行每列有且只有一个皇后棋子,每对角线至多一个皇后棋子。 如果使用回溯法,计算10皇后、20皇后问题还是可行的。 但是当皇后数增加到一百万个时,又该如何求解呢? 局部搜索算法用于求解组合优化问题,而皇后问题是组合问
-
如何用随机方法求解组合优化问题(一)
优化问题 设 (x) 是决策变量, (D) 是 (x) 的定义域, (f(x)) 是指标函数, (g(x)) 是约束条件。则优化问题可以表示为求解满足 (g(x)) 的 (f(x)) 最小值问题。即: [min_{xin D}(f(x)|g(x))] 组合优化问题 如果在定义域 (D) 上,满足约束条件 (g(x)) 的解的总数是有限的,则优
-
如何用随机方法求解组合优化问题(七)
这是一篇笔记,是对于B站up主马少平的视频(第四篇 如何用随机方法求解组合优化问题(七))的学习与记录。 一个商人要访问 (n) 个城市,每个城市访问一次,并且只能访问一次,最后再回到出发城市。 问如何规划才能使得行走的路径长度最短。 旅行商问题的解空间非
-
【数据库】— 无损连接、Chase算法、保持函数依赖
形式化定义: 构造一个 k k k 行 n n n 列的表格,每行对应一个模式 R i ( 1 ≤ i ≤ k ) Ri (1≤i ≤ k) R i ( 1 ≤ i ≤ k ) ,每列对应一个属性 A j ( 1 ≤ j ≤ n ) Aj( 1≤j≤ n) A j ( 1 ≤ j ≤ n ) ,若 A j Aj A j 在 R i Ri R i 中,则在表格的第 i i i 行第 j j j 列处填上 a j aj aj ,否则填上
-
OpenCV minMaxLoc()函数找出图像中最小值最大值
OpenCV 找出图像中最小值最大值函数minMaxLoc的使用 功能:从一个矩阵中找出全局的最大值和最小值。 函数cv::minMaxLoc找出最大和最小元素的值和他们的位置。极值是遍历整个矩阵找到,或者当掩码不是一个空矩阵时,是通过遍历指定矩阵区域找到。 函数不适用于多通道矩阵,
-
Python3 max() 函数 -求最大值、Python3 min() 函数 -求最小值
max() 方法返回给定参数的最大值,参数可以为序列。 以下是 max() 方法的语法: x -- 数值表达式。 y -- 数值表达式。 z -- 数值表达式。 返回给定参数的最大值。 以下展示了使用 max() 方法的实例: 尝试一下 以上实例运行后输出结果为: min() 方法返回给
-
10种基于MATLAB的方程组求解方法
线性方程组的求解包括直接法和迭代法,其中迭代法包括传统的高斯消元法,最速下降法,牛顿法,雅克比迭代法,共轭梯度法,以及智能启发式算法求解法和神经网络学习算法,传统算法可以相互组合改进,智能仿生启发式算法包括粒子群算法,遗传算法,模拟
-
【优化数学模型】2. 动态规划DP方法的求解思路
多阶段决策问题,就是要在允许的决策范围内,选择一个最优决策使整个系统在预定标准下达到最佳效果。 动态规划 (dynamic programming,DP) 是用来解决多阶段决策过程最优化的一种数量方法。其特点在于,它可以把一个n维决策问题变换为几个一维最优化问题,从而一个一个地去
-
VS依赖注入(DI)构造函数自动生成局部私有变量
依赖注入(DI)在开发中既是常见的也是必需的技术。它帮助我们优化了代码结构,使得应用更加灵活、易于扩展,同时也降低了各个模块之间的耦合度,更容易进行单元测试,提高了编码效率和质量。我们经常会先定义局部变量,再在构造函数中使用,每次都要这样去编写耗时
-
数学建模论文写作方法之一(模型的建立与求解)
一、模型的建立:(大多数都是根据实际问题套用别人已经建立的模型,但需要将问题与模型结合起来) 1.物理类问题中模型的建立 由。。。。知识的得到。。。。(公式) 2.优化类问题中模型的建立 ①目标函数+ ②约束条件 ③关于约束条件的说明 3.使用别人已经建立好的
-
数据结构学习记录——判断是否为同一颗二叉搜索树(题意理解、求解思路、程序搭建框架、具体函数的实现)
目录 题意理解 问题 描述 输入样例 输出样例 求解思路 建两棵二叉树 不建树 建一棵树 搜索树表示 程序框架搭建 如何建搜索树 如何判别 方法 查找函数 判断函数 其他函数 给定一个插入序列就可以唯一确定一颗二叉搜索树。 但是,一颗给定的二叉搜索树却可以由多种不同
-
密码学——Hill体制密码中已知明文M和密文C求解密钥矩阵K的两种方法之逆矩阵求解法和待定系数求解法
本文主要解决古典密码中的Hill体制密码在已知明文M和密文C的情况下求解密钥矩阵K的两种方法:①求逆矩阵②待定系数法。 如若不懂Hill体制的古典密码可以参照我上一篇文章密码学——几种典型的古典密码体制(Caesar体制、Playfair体制、Vigenere体制、Beaufort体制以及Hill体制)
-
机器学习笔记之最优化理论与方法(九)无约束优化问题——常用求解方法(下)
上一节介绍了 牛顿法、拟牛顿法 。本节将继续以 拟牛顿法 为基础,介绍 DFP , BFGS text{DFP},text{BFGS} DFP , BFGS 方法 。 经典牛顿法缺陷与修正牛顿法 关于 经典牛顿法 中关于 下降方向 D k ( k = 1 , 2 , ⋯ , ∞ ) mathcal D_k(k=1,2,cdots,infty) D k ( k = 1 , 2 , ⋯ , ∞ ) 的 数学符号 表