最小函数依赖集题目是什么
-
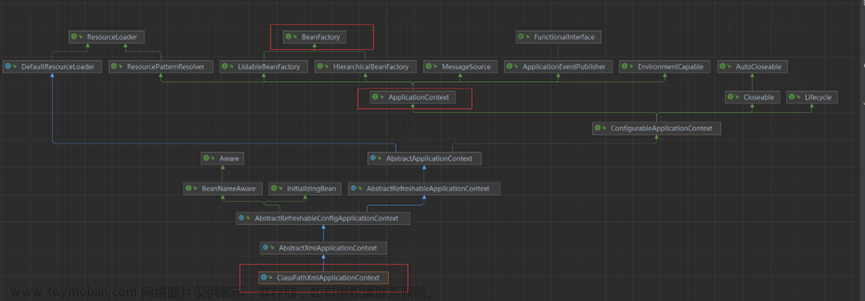
什么是Spring的IoC,依赖注入又该怎么实现?
什么是IoC 所谓的控制反转(Inversion of Control),缩写为IoC,其实就是把对象的创建和对象之间的依赖关系处理,交给 Spring容器来管理,不用程序员自己创建和维护的一种技术。我们使用IoC的目的,主要是为了降低类之间的耦合。 IoC的底层原理 IoC的底层原理主要是基于xml解析+工
-
单链表功能函数练习——按规定插入指定节点及删除最小值节点(C语言)
* 函数名称: LList_DestInsert * 函数功能: 在指定值位置处,插入指定的数据data * 函数参数: LList_t *Head: 需要操作的链表头节点 DataType_t dest: 插入位置的值 DataType_t data: 需要插入的指定的数据 * 返回结果: true or false * 注意事项: None * 函数作者: ni456xinmie@163.com * 创建日期:
-
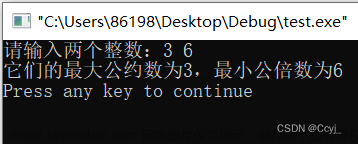
实验五 C语言函数程序设计习题 (使用函数计算两点间的距离,请编写函数fun,使用函数输出字符矩阵,使用函数求最大公约数和最小公倍数)
1. 使用函数计算两点间的距离:给定平面任意两点坐标(x1,y1)和(x2,y2),求这两点之间的距离(保留2位)小数。要求定义和调用dist(x1,y1,x2,y2)计算两点间的距离。坐标中两点坐标之间的距离公式如下: 2. 请编写函数fun,它的功能是计算并输出给定整数n的所有因子(不包括1与自身)
-
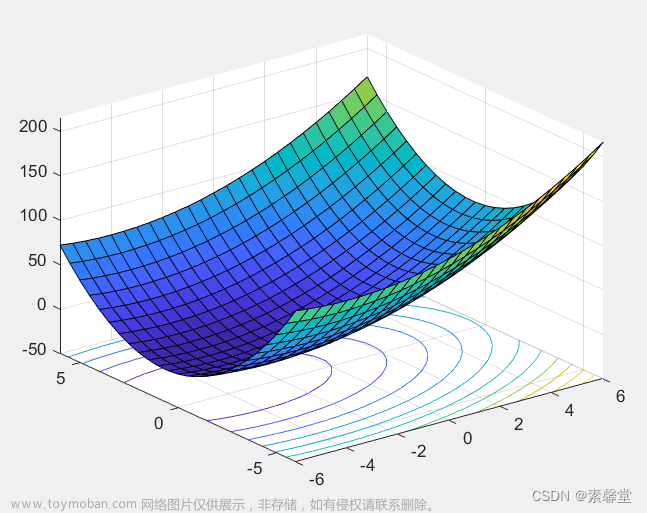
35.利用fminsearch解 多元变量无约束条件下的函数最小值(matlab程序)
1. 简述 函数功能:使用无导数法计算无约束多变量函数的最小值 2. 代码 主程序: % 通过绘图确定一个初始值;然后进行迭代找到真正的最小值; clc clear [x,y]=meshgrid(-6:.5:6); f= 8*x-4*y +x.^2+3*y.^2; surfc(x,y,f) x0=[0,0]; %[x,fval,exitflag]=fminunc(@(x)(8*x(1)-4*x(2) +x(1).^2+3*x(2).^2
-
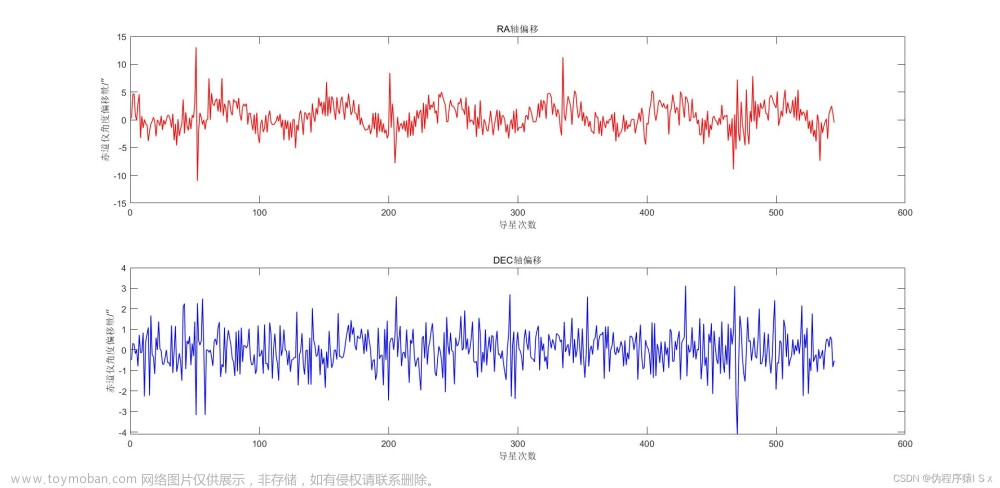
C++类:三角函数最小二乘拟合与离散傅里叶变换求解
作为一个天文爱好者,在之前全手工制作了一个天文望远镜导星的系统,但是由于自制的赤道仪使用的是谐波减速器,赤经轴需要一直保持与地球运动同步,每隔一段时间就会有新的谐波齿轮参与啮合,因此造成了在赤经轴存在低频的传动周期误差,该系统利用图像
-
【Python】人工智能-机器学习——不调库手撕演化算法解决函数最小值问题
现在有一个函数 3 − s i n 2 ( j x 1 ) − s i n 2 ( j x 2 ) 3-sin^2(jx_1)-sin^2(jx_2) 3 − s i n 2 ( j x 1 ) − s i n 2 ( j x 2 ) ,有两个变量 x 1 x_1 x 1 和 x 2 x_2 x 2 ,它们的定义域为 x 1 , x 2 ∈ [ 0 , 6 ] x_1,x_2in[0,6] x 1 , x 2 ∈ [ 0 , 6 ] ,并且 j = 2 j=2 j = 2 ,对于此例,所致对于 j =
-
【重新定义matlab强大系列八】利用matlab求局部值(函数islocalmax求局部最大值+函数islocalmin求局部最小值)
🔗 运行环境: Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印—— 左手の明天 #### 💗 大家好🤗🤗🤗,我是 左手の明天 !好久不见💗 💗今天开启新的系列——
-
LeetCode 0746. 使用最小花费爬楼梯:动态规划(原地)——不用什么从递归到递推
力扣题目链接:https://leetcode.cn/problems/min-cost-climbing-stairs/ 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你计算并返回达到楼
-
极简的输入_求最小值的函数_求和的函数_矩阵_1879_B. Chips on the Board
还在想应该怎么算,原来这么简单 要求每一行或者每一列都有元素 每一行都有元素的话,答案就是所有 A 的和再加上 n 个 B 的最小值的和 每一列都有元素的话,答案就是所有 B 的和再加上 n 个 A 的最小值的和 最后取上面两个和的最小值 有一种代码非常简短的写法,输入的
-
利用Microsoft Visual Studio查看.dll文件的依赖项及内部函数名
对于安装了Microsoft Visual Studio的,可以点开电脑左下角Windows图标,在Visual Studio里找到VS 20xx开发人员命令提示符,打开后可以看到当前路径是Visual Studio的安装路径,如果你的.dll文件存放在另一磁盘(比如C盘),先输入C:,再回车进入C盘,然后用 命令更改路径到你的.dll文件所
-
麻雀算法SSA,优化VMD,适应度函数为最小包络熵,包含MATLAB源代码
针对大家评论区给出的很多问题,作者一直都有关注,因此在这里又写了一篇文章,而且思路与这篇文章有不同之处,至于具体的不同之处放在下一篇文章了,大家感兴趣的可以移步观看,下一篇文章可以说是 作者的呕心力作。 (4条消息) 白鲸优化算法优化VMD参数,并提取特
-
详解Leetcode中关于malloc模拟开辟二维数组问题,涉及二维数组的题目所给函数中的各个参数的解读
最近博主一直再刷Leetcode上有关c语言的题目,有些题目第一步就将我卡死了。为什么呢?因为题目中所给的函数里的参数的具体含义我既然都不知道是什么意思。当然在请教了一些大佬后我也顺利解决了,不然也不会有人和你们分享了,哈哈哈~ 我就已一个典型的题目来介绍
-
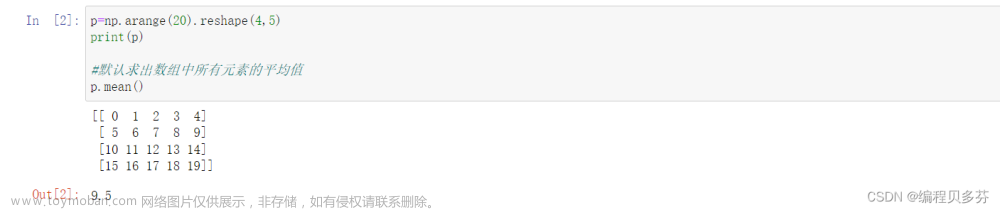
Numpy中统计函数的讲解:平均值、中位数、标准差、方差、最大最小值、求和、加权平均数
目录 统计函数: Numpy 能方便地求出统计学常见的描述性统计量 一:Numpy中统计函数--平均值 求平均值 二:Numpy中统计函数--中位数 中位数 np.median 平均数和中位数的区别 三:Numpy中统计函数--标准差 求标准差ndarray.std() 四:Numpy中统计函数--方差 求方差ndarray.var() 标准差和方差
-
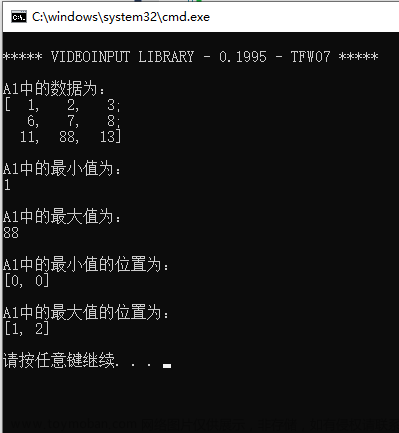
利用OpenCV的函数minMaxLoc()获取图像中像素的最小值、最大值以及对应的坐标值
函数minMaxLoc()的原型如下: C++原型: Python原型: 参数意义很简单,官方文档原文如下: src—input single-channel array. minVal—pointer to the returned minimum value; NULL is used if not required. maxVal—pointer to the returned maximum value; NULL is used if not required. minLoc—pointer to the returned minimum location (in
-
Spring 为什么要用三级缓存来解决循环依赖(AOP),二级缓存不行吗
解决有代理对象的循环依赖不一定要三级缓存,用二级甚至一级也能解决,下面讨论下Spring为什么选择三级缓存这个方案。 Spring最开始是没有三级缓存的,后面版本因为引入了AOP,有了代理对象,又因为存在循环依赖,为了保证依赖注入过程注入的是代理对象,且不完全打破
-
Qt 自定义窗口的标题栏,重写鼠标事件实现,关闭隐藏,最大化/最小化,重写窗口事件函数,实现鼠标选中边框拉大拉小,双击标题栏切换窗口最大化和最小化
Qt 自定义窗口的标题栏,重写鼠标事件实现,关闭隐藏,最大化/最小化,重写窗口事件函数,实现鼠标选中边框拉大拉小,双击标题栏切换窗口最大化和最小化 1、main.cpp 2、widget.h 3、widget.cpp 4、效果展示 5、完成
-
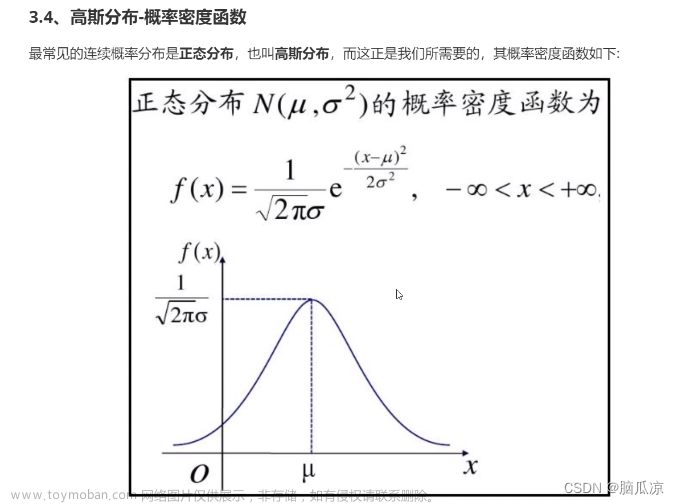
人工智能基础_机器学习007_高斯分布_概率计算_最小二乘法推导_得出损失函数---人工智能工作笔记0047
这个不分也是挺难的,但是之前有详细的,解释了,之前的文章中有, 那么这里会简单提一下,然后,继续向下学习 首先我们要知道高斯分布,也就是,正太分布, 这个可以预测x在多少的时候,概率最大 要知道在概率分布这个,高斯分布公式中,u代表平均值,然后西格玛代表标准差,知道了
-
Docker[1] Docke环境是什么 安装部署 依赖兼容解决 简介 Centos安装Docker 配置镜像加速 启动Docker
1.1.什么是Docker 微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。 ● 分布式系统中,依赖的组件非常多,不同组件之间部署时往往会产生一些冲突。 ● 在数百上千台服务中重复部署,环境不一定一致,会遇到各种问题 1.1.1.应用部署的环境问题
-
报错:在从 Git 上拉取代码后,使用 npm install 安装依赖失败,但使用 yarn 可以成功安装,这是为什么
在从 Git 上拉取代码后,使用 npm install 安装依赖失败,但使用 yarn 可以成功安装的原因可能有多种,以下是一些常见原因: 安装的依赖库版本不兼容。有时候,package.json 文件中的依赖库版本与本地或全局的 Node.js 环境不兼容,或与已安装的其他依赖库的版本不兼容,在使用





![Docker[1] Docke环境是什么 安装部署 依赖兼容解决 简介 Centos安装Docker 配置镜像加速 启动Docker](https://imgs.yssmx.com/Uploads/2024/04/846951-1.png)