求矩阵的秩阶梯
-
基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度(matlab代码)
目录 1 主要内容 系统结构图 P2G-CCS 耦合模型 其他算例对比 2 部分代码 3 下载链接 该程序复现《基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度》模型,以碳交易和碳封存成本、燃煤机组启停和煤耗成本、弃风成本、购气成本之和为目标函数,考虑了功率平衡
-
【EI复现】基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度(Matlab代码实现)
💥💥💞💞 欢迎来到本博客 ❤️❤️💥💥 🏆博主优势: 🌞🌞🌞 博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️ 座右铭: 行百里者,半于九十。 📋📋📋 本文目录如下: 🎁🎁🎁 目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码、数据及文章
-
【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数
单纯矩阵 :A可对角化⇔①A可对角化;⇔②n个线性无关的特征向量; ⇔③每个特征值的几何重复度等于代数重复度;⇔④特征值λi对应的pi = n - rank(λiE - A)。 等价矩阵 :A(λ)等价于B(λ)⇔① 任意k阶行列式因子相同Dk(λ);⇔②有相同的不变因子dk(λ);⇔③相同的初等因子,且
-
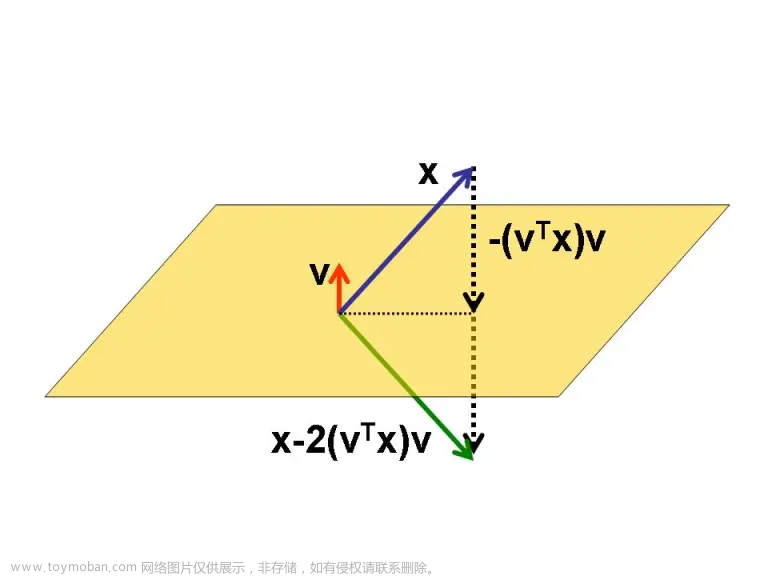
矩阵理论| 特殊矩阵:Householder矩阵 / 镜射矩阵
由来:镜射变换 给定 镜射超平面,其法向量为 v bold v v ( ∥ v ∥ = 1 |bold v|=1 ∥ v ∥ = 1 ) 对于任意向量 x bold x x ,其镜射变换后的向量为 x − 2 v ( v T x ) = ( I − 2 v v T ) x mathbf{x}-2mathbf{v}(mathbf{v}^Tmathbf{x})=(I-2mathbf{v}mathbf{v}^T)mathbf{x} x − 2 v ( v T x ) = ( I − 2 v v T ) x (
-
矩阵理论| 特殊矩阵:Hermite矩阵/共轭对称矩阵
Hermite矩阵是复数域上的“对称矩阵” Hermite矩阵性质 其性质 与实对称矩阵基本一致 : 实数特征值; 有一套正交的特征向量(各个特征子空间正交+代数重数=几何重数) 此外,Hermite矩阵也是复正定矩阵的前提(就如实数域中对称矩阵是正定矩阵的前提): A boldsymbol{A} A 为
-
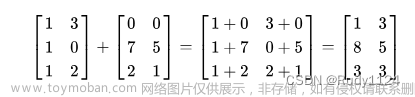
矩阵乘法(矩阵乘矩阵)
首先理了解矩阵是什么: 矩阵是一个按照长方阵列排列的复数或实数集合。(相信大家都懂) 关于矩阵的基本概念: 1.方阵:n 阶方阵 (正方形嘛) 2.同型矩阵:两个矩阵,行数与列数对应相同,称为同型矩阵 矩阵加减法: 在了解矩阵乘法前先看看矩阵加减法: 1.两个矩阵
-
矩阵理论| 特殊矩阵:正定矩阵
实数域中,满足 x T A x 0 ( x ≠ 0 ) mathbf{x}^{T} boldsymbol{A} mathbf{x}0 quad(mathbf{x}neq 0) x T A x 0 ( x = 0 ) 的矩阵 A boldsymbol{A} A 就是正定矩阵; 在复数域,满足 x H A x 0 ( x ≠ 0 ) mathbf{x}^{H} boldsymbol{A} mathbf{x}0 quad(mathbf{x}neq 0) x H A x 0 ( x = 0 ) 的矩阵 A boldsymbol{A} A 就是正定矩
-
数据结构-拓展突破-特殊矩阵(对称矩阵,三角矩阵,三对角矩阵,稀疏矩阵)的压缩存储)
对称矩阵的定义: 若n阶方阵中任意一个元素a,都有a(i,j)=a(j,i)则该矩阵为对称矩阵 也就是说对称矩阵的元素关于对角线对称。对角线上半部分称为上三角区,下半部分称为下三角区。 对称矩阵的压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区) 可以定义一维数
-
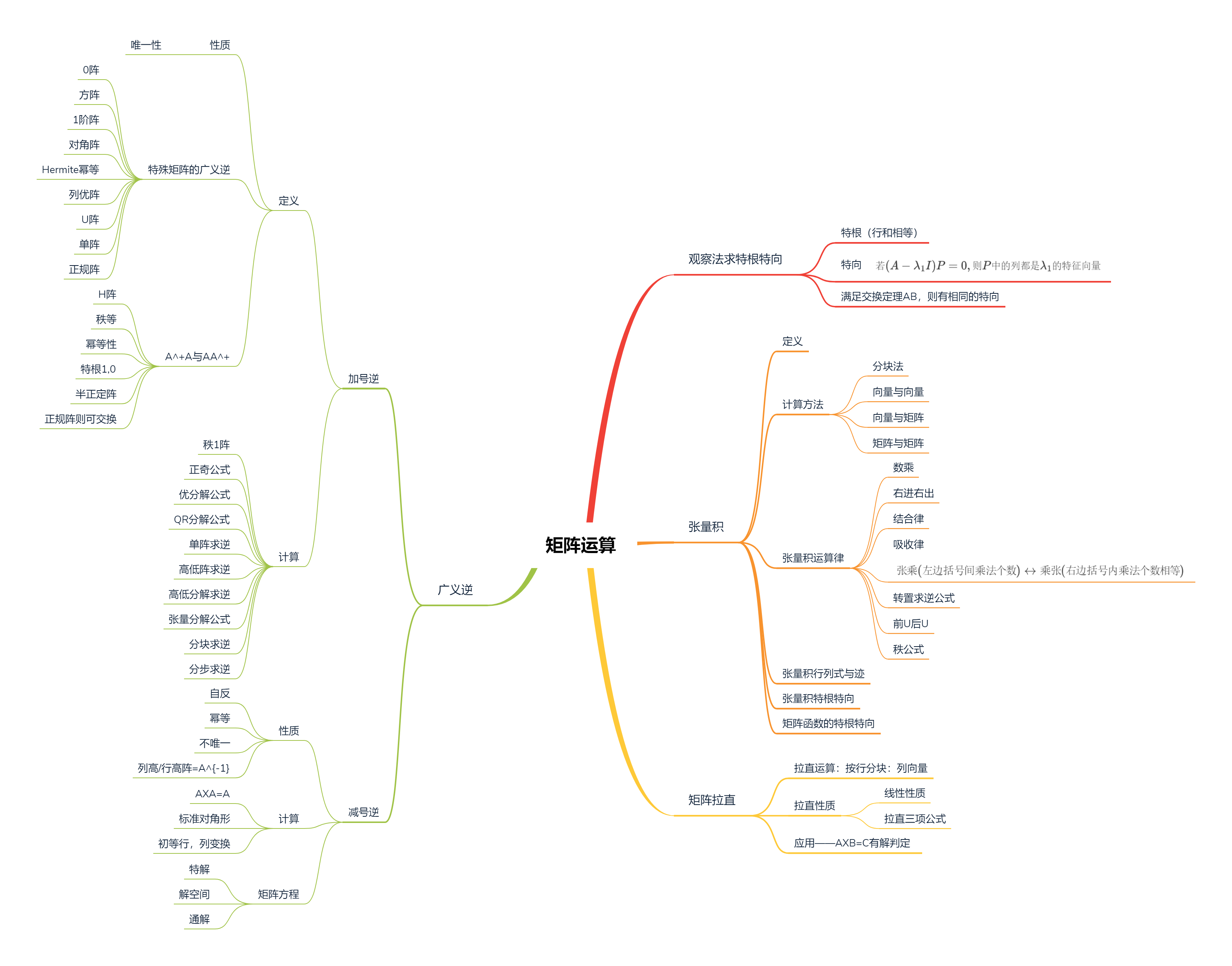
【矩阵论】4. 矩阵运算——矩阵拉直
矩阵论的所有文章,主要内容参考北航赵迪老师的课件 [注]由于矩阵论对计算机比较重要,所以选修了这门课,但不是专业搞数学的,所以存在很多口语化描述,而且对很多东西理解不是很正确与透彻,欢迎大家指正。我可能间歇性忙,但有空一定会回复修改的。 矩阵论 1
-
转置矩阵、对称矩阵、反对称矩阵以及向量的反对称矩阵
假设矩阵 A 如下表示: 则其转置矩阵表示为: 若矩阵 B 与其转置矩阵相等,则称矩阵 B 为对称矩阵,如: 若矩阵 C 与其转置矩阵取负后相等,则称矩阵 C 为反对称矩阵,其对角线元素的值为0,如: 分别定义两个向量如下: 对两个向量进行叉乘得到: 则向量的反对称矩阵为
-
特殊矩阵的压缩存储(对称矩阵,三角矩阵和三对角矩阵)
目录 1.对阵矩阵 2.三角矩阵 3.三对角矩阵(带状矩阵) 定义:若对一个n阶矩阵A中的任意一个元素 aᵢ,ⱼ 都有aᵢ,ⱼ=aⱼ,ᵢ (1≤i,j≤n),则称其为对称矩阵。 存储策略:只存储主对角线+下三角区(或主对角线+上三角区),以主对角线+下三角区为例,按照行优先把这些元
-
矩阵转置与随机矩阵: 涉及到高斯矩阵和霍夫矩阵
矩阵转置和随机矩阵是线性代数和概率论中的基本概念。在大数据领域,这些概念在数据处理和机器学习中具有重要的应用。高斯矩阵和霍夫矩阵则是随机矩阵的特殊情况,它们在信息论、统计学和机器学习等领域具有广泛的应用。本文将详细介绍这些概念的定义、性质、算
-
python生成特殊矩阵:循环矩阵、汉克尔矩阵、费德勒矩阵……
scipy.linalg 中提供了一系列特殊矩阵的生成方法,包括循环矩阵、汉克尔矩阵、费德勒矩阵、阿达马矩阵、莱斯利矩阵、希尔伯特及其逆矩阵、帕斯卡及其逆矩阵等。 现有一向量 c = [ c 0 , c 1 , ⋯ , c n ] c=[c_0, c_1,cdots,c_n] c = [ c 0 , c 1 , ⋯ , c n ] ,则 circulant(c) 返回一
-
矩阵运算_矩阵的协方差矩阵/两个矩阵的协方差矩阵_求解详细步骤示例
在统计学中, 方差 是用来度量 单个随机变量 的 离散程度 ,而协方差则一般用来刻画 两个随机变量 的 相似程度。 参考: 带你了解什么是Covariance Matrix协方差矩阵 - 知乎 将输入数据A进行中心化处理得到A\\\'。即通过 减去每个维度的平均值 来实现中心化。 注意:
-
【矩阵论】3. 矩阵函数——矩阵函数求导
矩阵论的所有文章,主要内容参考北航赵迪老师的课件 [注]由于矩阵论对计算机比较重要,所以选修了这门课,但不是专业搞数学的,所以存在很多口语化描述,而且对很多东西理解不是很正确与透彻,欢迎大家指正。我可能间歇性忙,但有空一定会回复修改的。 矩阵论 1
-
邻接矩阵、可达性矩阵、完全关联矩阵、可达性矩阵的计算
邻接矩阵:很简单,就是两个点有关系就是1,没有关系就是0 可达性矩阵:非常简单,两点之间有路为1,没有路为0 可发行矩阵的计算 :有n个元素,初始可达性矩阵为A,那么最终的矩阵 B= 完全关联矩阵:描述点与边的关系,如果该点和该边有关系为1,没有关系就为0,非常
-
回型矩阵|蛇形矩阵|上三角矩阵|矩阵转置|二维数组打印问题
二维数组,作为一种存放一系列数的载体,不免和数学中用于存放数的数表——矩阵,有着密切的联系。矩阵本身就有些抽象,需要设计一个程序精准打印出来更是有难度,所以今天便来总结一些二维数组与矩阵打印的问题该如何解决。 (题目取自牛客网BC133-BC138) 给你一个
-
螺旋矩阵、旋转矩阵、矩阵Z字打印
类似于这个螺旋矩阵我们也是在每次处理最外层的矩形,然后往内收缩。 对于一个矩形我们选取四个点依次进行交换即可 也是和螺旋矩阵类似选取两个点进行循环
-
【数据结构】特殊矩阵的压缩存储(对称矩阵,三角矩阵和三对角矩阵)
目录 1.对阵矩阵 2.三角矩阵 3.三对角矩阵(带状矩阵) 定义:若对一个n阶矩阵A中的任意一个元素 aᵢ,ⱼ 都有aᵢ,ⱼ=aⱼ,ᵢ (1≤i,j≤n),则称其为对称矩阵。 存储策略:只存储主对角线+下三角区(或主对角线+上三角区),以主对角线+下三角区为例,按照行优先把这些元
-
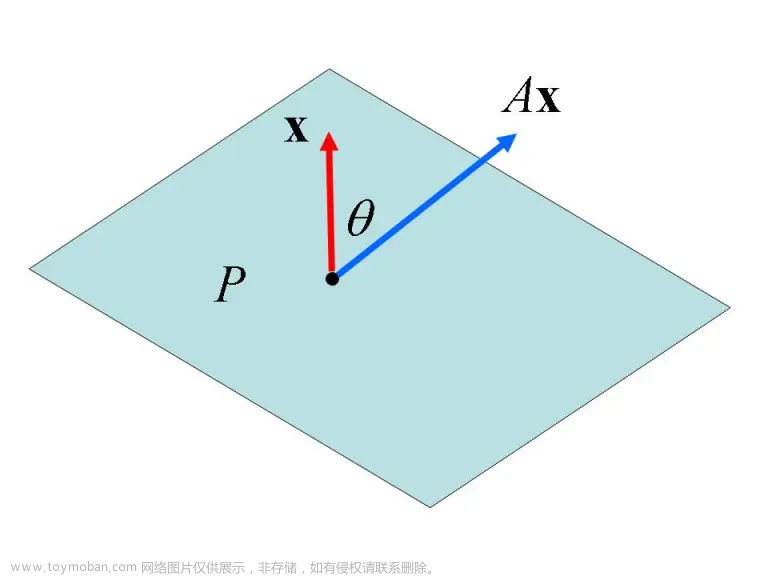
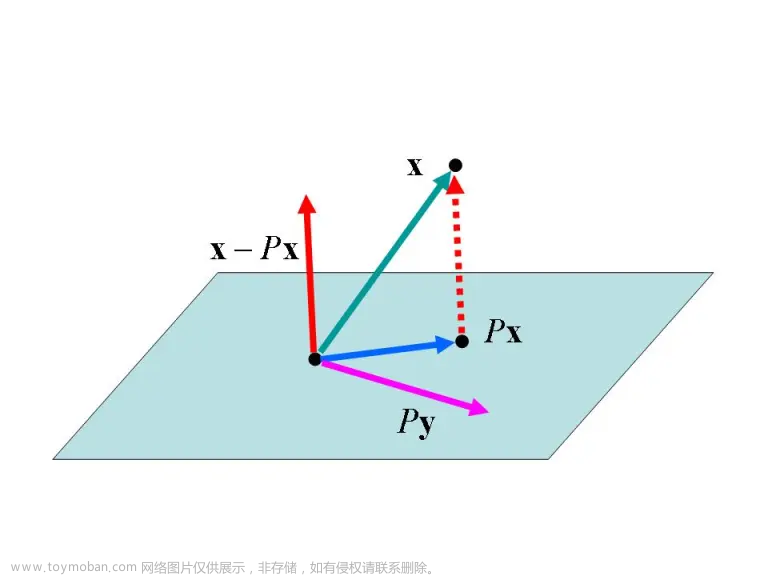
矩阵理论| 特殊矩阵:幂等矩阵、投影、正交投影
投影矩阵 /幂等矩阵 (idempotent matrix) P mathbf P P 满足 P 2 = P P^2=P P 2 = P ,也即 P ( I − P ) = 0 P(I-P)=0 P ( I − P ) = 0 幂等矩阵 P P P 的几何意义:将向量 x mathbf{x} x 投影至 P P P 的列空间 C ( P ) C(P) C ( P ) 内 而 P 2 = P P^2=P P 2 = P 的意义就是“投影两次等效于投影一次” 投影也分为两