秩和检验编秩原则
-
Hosmer-Lemeshow检验(HL检验)
Hosmer-Lemeshow检验(HL检验) 为模型拟合指标,其原理在于判断预测值与真实值之间的gap情况,如果p值大于0.05,则说明通过HL检验,即说明预测值与真实值之间并无非常明显的差异。反之如果p值小于0.05,则说明没有通过HL检验,预测值与真实值之间有着明显的差异,即说明模
-
参数检验和非参数检验(结合SPSS分析)
概念 :是一种根据样本数据来推断总体的分布或均值、方差等总体统计参数的方法。 根据 样本 来推断 总体 的原因: 总体数据不可能全部收集到。如:质量检测问题 收集到总体全部数据要耗费大量的人力和财力 假设检验包括: 参数检验 非参数检验 基本原理 :利用小概率
-
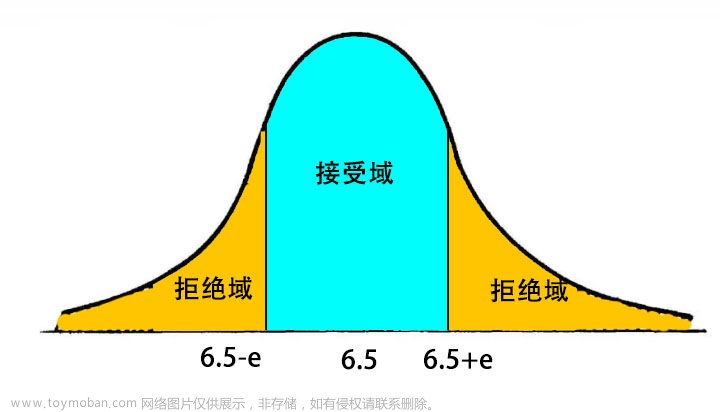
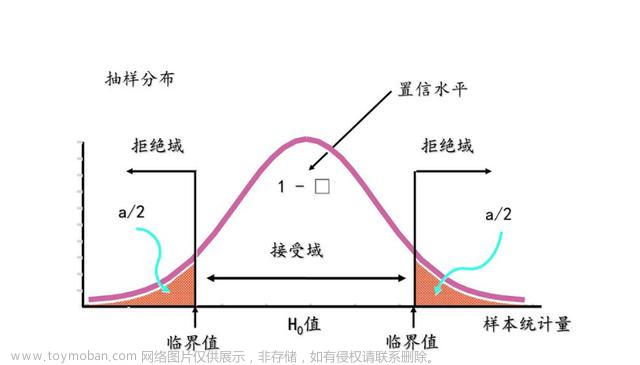
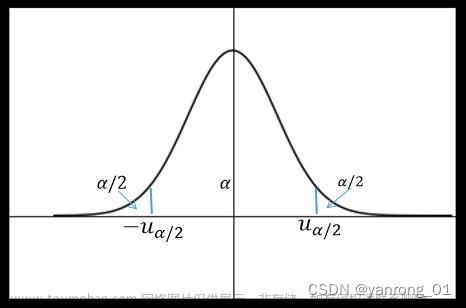
假设检验:如何理解单侧、双侧检验的拒绝域
简单说就是:拒绝域与备择假设方向相同。假设检验就是一个证伪的过程,原假设和备择假设是一对\\\"相反的结论\\\"。\\\"拒绝域\\\",顾名思义,就是拒绝原假设的范围和方向,所以判断拒绝域在哪,可以直接看备择假设H1的条件是大于还是小于即可。 上述只是判断方法之一
-
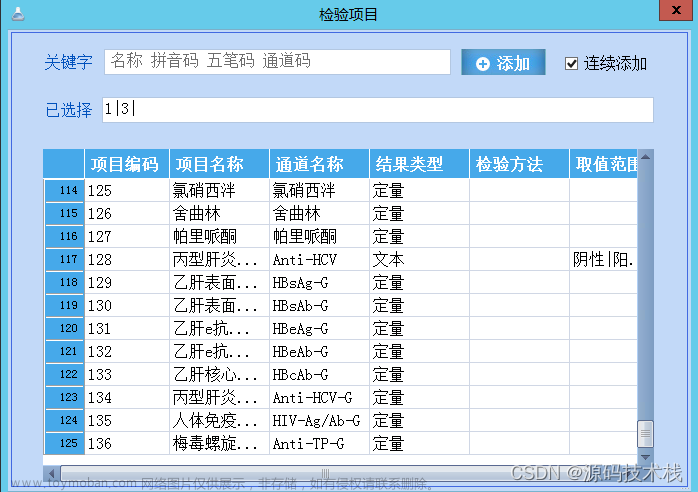
医院检验科LIS系统的常规检验项目有哪些?
白细胞数目、中性粒细胞数目、淋巴细胞数目、单核细胞数目、嗜酸性粒细胞数目、嗜碱性粒细胞数目、中性粒细胞百分比、 淋巴细胞百分比、单核细胞百分比、嗜酸性粒细胞百分比、嗜碱性粒细胞百分比、红细胞数目、血红蛋白、红细胞压积、平均红细胞体积、 平均红
-
显著性检验【t-test、方差分析、ks检验】
1显著性检验基本定义(what?) 2.使用显著性检验的意义(why? ) 3.显著性检验的具体操作流程(how? ) 统计假设检验(Statistical hypothesis testing) 事先对总体(随机变量)的 参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设是否合理 显著性检验(signific
-
正态分布检验:检验序列数据是否符合正态分布
介绍 JB检验主要适用于 样本数量大于30 ,而且样本数越多,JB检验效果越准确。 JB检验主要用于 判断数据是否符合总体正态分布 ,而且构造的 JB统计量 需要符合自由度为2的卡方分布,即为 。JB统计量如下所示。 (n为样本量,S为偏度,K为峰度) JB检验主要 利用峰度 和 偏
-
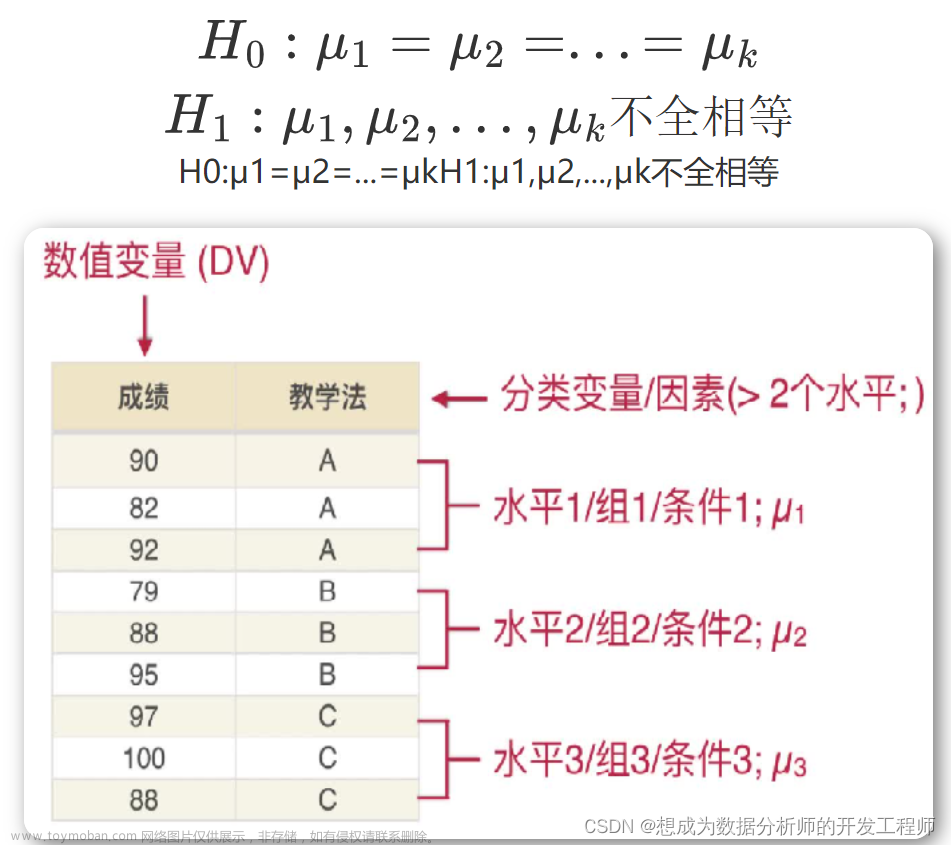
6.方差分析——单因素检验、事后检验的数学公式与代码实现
方差分析(Analysis of Variance,ANOVA)是假设检验的一种延续与扩展,主要用来对多个总体均值(三组或三组以上均值)是否相等作出假设检验,研究分类型自变量对数值型因变量的影响。 它的零假设和备择假设分别为: 方差分析的核心 因变量的总变化由两部分引起: 自变量引起
-
时间序列之单位根检验+显著性检验+固定/随机效应模型选择
确定时间分隔、开始时间、结束时间 在hive中创建该表 计算每段时间内申购和赎回的量 查询每段时间开始和结束时的万份收益,计算净收益率 在面板数据和序列数据中,如果存在单位根,会产生 伪回归 等严重后果,所以必须对每个变量进行单位根检验,这样能够保证每个变
-
非参数检验-Wilcoxon,Wilcoxon-Mann-Whitney符号秩检验以及Pearson,Spearman秩,Kendall τ相关检验(附带实例-R实现)
符号检验是非参数统计中最古老的检验方法之一,这种检验被称为符号检验的一个理由是它所关心的信息只与两类观测值有关,如果用符号“+”和“-”区分,符号检验就是通过符号“+”和“-”的个数进行统计推断。符号检验的推断过程(以双边检验为例): 从1.1符号检验
-
QMS质量检验管理|攻克制造企业质量检验难题,助力企业提质增效
在日益激烈的市场竞争中,对产品质量严格把关,是制造企业提高核心竞争力与品牌价值的关键因素。那如何高效、高质地完成产品质检工作?这就需要企业在工业质检中引进数字化技术加以辅助,进而推动智能制造高质量发展。 蓝库云QMS质量检验管理系统,涵盖来料检验、
-
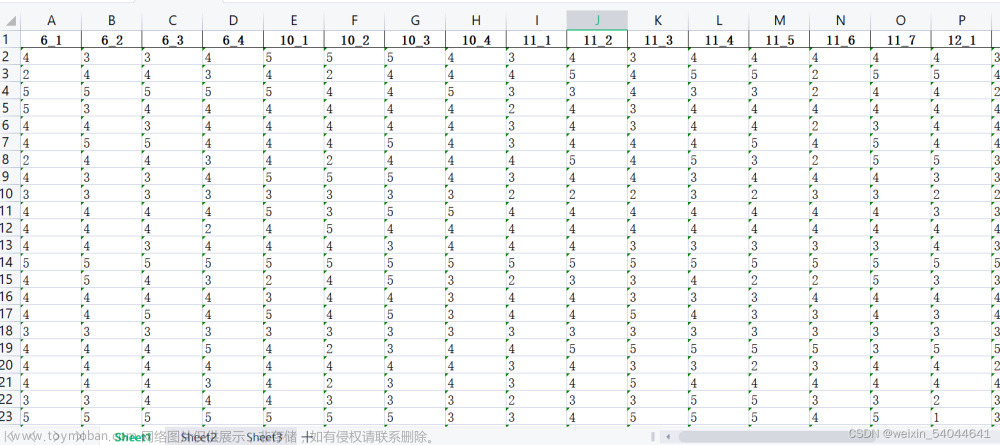
利用Python进行调查问卷的信度检验和效度检验,并对量表进行因子分析
关于问卷是否需要进行问卷信效度检验,前提时你的问卷含有量表题,量表题有两种量表:李克特量表和瑟斯顿量表 ,并且只有量表题才参与信效度检验。所以,信效度检验前需要对量表每一个选项的得分数据放到独立的一列数据中。如下图所示(Excel表) 我们说量表的信度
-
面向对象设计的六大原则(SOLID原则)-——单一职责原则
单一职责原则(Single Responsibility Principle, SRP)是面向对象编程和设计的五大SOLID原则之一。它强调一个类、方法或模块应该只有一个职责,即只做一件事情。如果一个类承担的职责过多,那么它的可维护性、可读性和可扩展性都会受到影响。当需要修改类的某个职责时,可能
-
面向对象设计的六大原则(SOLID原则)-——开闭原则
开闭原则(Open-Closed Principle, OCP)是面向对象设计的五大SOLID原则之一。这个原则主张“软件实体(类、模块、函数等)应该对扩展开放,对修改关闭”。也就是说,软件的设计应该允许在不修改原有代码的情况下增加新的功能。这样的设计有助于降低代码的复杂性和维护成本
-
深度学习记录--梯度检验
为了对梯度进行检验,需要计算近似误差值来接近梯度 对于单边误差和双边误差公式,其中双边误差与真实梯度相差更小,故一般采用双边误差公式 双边误差 公式: 对于成本函数,求出的导数,计算出双边误差 ,再将两者进行比较 比较方法: ,判断的大小 若,则误差很
-
Python快速检验数据分布
假设检验的前提是确定数据的分布,本文介绍Python检验数据样本是否服从一定分布。使用方法是柯尔莫可洛夫-斯米洛夫检验(Kolmogorov–Smirnov test,K-S test),K-S检验方法适用于探索连续型随机变量的分布,对于离散分布(二项分布和泊松分布)需要使用其他方法进行检验。
-
数学建模.假设检验
一.步骤 1.96为作用域,下面是作用域求法 在置信度为95%的情况下显然是不成立的,那么我们可以看看在置信度为99%的情况下结果如何呢 可以看到在置信度为99%的情况下是94斤是可以被认为偶然的误差,但是这个作用域不是很好计算,所以引用p值的方法,方法如下: 由此观之
-
数学建模-假设检验
原假设,备择假设 P值,显著性水平 单侧建议,双侧检验
-
假设检验(hypothesis testing)
首先,什么是假设?在数理推断中,总体分布通常是未知的,包含了两类,一类是分布类型未知,一类是分布类型已知,但参数未知, 假设 就是对总体分布的一种推断,比如假设总体服从正态分布,假设正态分布的均值是500。根据未知类型,分为非参数假设和参数假设。 假
-
【统计】假设检验方法
1. 不同检验方法 最小样本量 的确认 由统计量反推得到 2. 检验方法 方差齐性检验(F检验): 两个独立样本的方差差异检验,反映了平均值的代表性。方差齐次检验前提要近似正态分布。 正态性检验: 是否符合正态分布 似然比检验: 比较样本不同似然函数,检验其分布 参
-
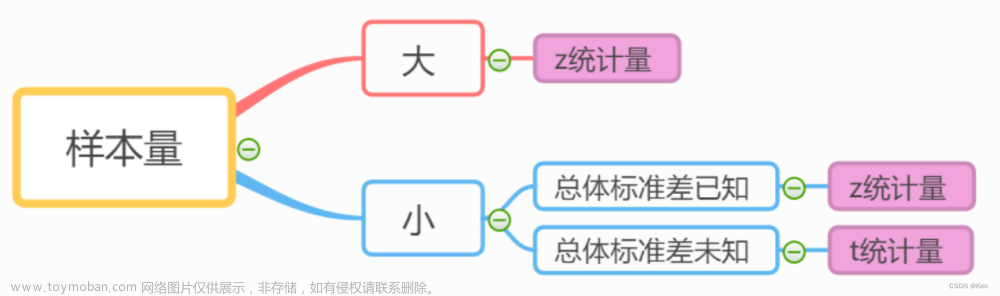
python统计(二)假设检验
DescrStatsW.ztest_mean() statsmodels.stats.weightstats.DescrStatsW.ztest_mean(value=0, alternative=\\\'two-sided\\\') 参数 说明 value 假设的均值 alternative 备择假设的形式,可选值:‘two-sided’, ‘larger’, ‘smaller’ weightstats.ztest() statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative=\\\'two-sided\\\') 参数 说明