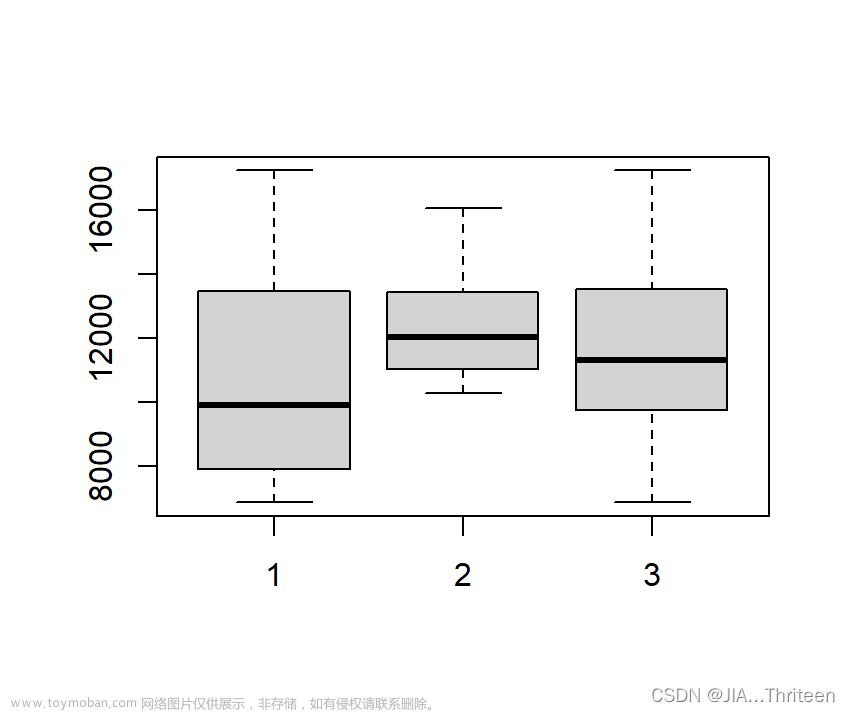
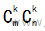秩和比法 编秩的说法正确的是
-
非参数统计:两样本和多样本的Brown-Mood中位数检验;Wilcoxon(Mann-Whitney)秩和检验及有关置信区间;Kruskal-Wallis秩和检验
目录 两样本和多样本的Brown-Mood中位数检验 例3.1我国两个地区一些(分别为17个和15个)城镇职工的工资(元): Wilcoxon(Mann-Whitney)秩和检验及有关置信区间 例3.1我国两个地区一些(分别为17个和15个)城镇职工的工资(元): Kruskal-Wallis秩和检验 例4.1在一项健康实验中,三人组
-
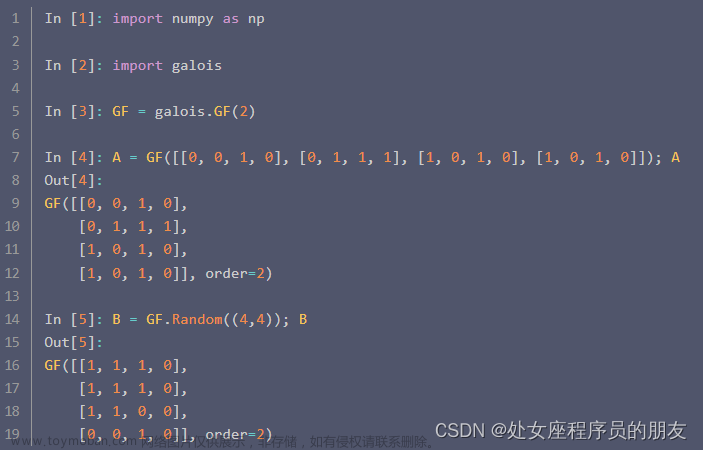
GF(2)上矩阵秩的快速计算
https://github.com/mhostetter/galois/issues
-
线性代数之矩阵秩的求法与示例详解
线性代数之矩阵秩的求法 在m×n的矩阵A中,任取k行、k列(k小于等于m、k小于等于n),位于这些行和列交叉处的 个元素,在不改变原有次序的情况下组成的矩阵叫做矩阵A的k阶子式。 不难发现矩阵A有个 个k阶子式。 比如有矩阵A 比如取第1行,第3行,第1列,第4列交叉上的元素
-
6.利用matlab完成 符号矩阵的秩和 符号方阵的逆矩阵和行列式 (matlab程序)
1. 简述 利用 M 文件建立矩阵 对于比较大且比较复杂的矩阵,可以为它专门建立一个 M 文件。下面通过一个简单例子来说明如何利用 M 文件创建矩阵。 例 2-2 利用 M 文件建立 MYMAT 矩阵。 (1) 启动有关编辑程序或 MATLAB 文本编辑器,并输入待建矩阵: (
-
解密Python求矩阵秩的算法与实用指南:从基础到高阶方法
在线性代数和计算机科学中,矩阵秩是一个重要的概念,它反映了矩阵中线性无关的行或列的数量,从而揭示了矩阵的重要性质。Python 作为一门强大的编程语言,提供了多种方法来求解矩阵的秩。本文将深入探讨 Python 中求解矩阵秩的算法,从基础的高斯消元法到高阶的 SV
-
【考研数学】线形代数第三章——向量 | 3)向量秩的性质、向量空间、过渡矩阵
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 性质 1(三秩相等) —— 设 A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n ) T pmb{A=(beta_1,beta_2,dots,beta_n)=(alpha_1,alpha_2,dots,alpha_n)^T} A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n )
-
【考研数学】线形代数第三章——向量 | 3)向量组秩的性质、向量空间、过渡矩阵
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 性质 1(三秩相等) —— 设 A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n ) T pmb{A=(beta_1,beta_2,dots,beta_n)=(alpha_1,alpha_2,dots,alpha_n)^T} A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n )
-
44、Flink之module模块介绍及使用示例和Flink SQL使用hive内置函数及自定义函数详细示例--网上有些说法好像是错误的
一、Flink 专栏 Flink 专栏系统介绍某一知识点,并辅以具体的示例进行说明。 1、Flink 部署系列 本部分介绍Flink的部署、配置相关基础内容。 2、Flink基础系列 本部分介绍Flink 的基础部分,比如术语、架构、编程模型、编程指南、基本的datastream api用法、四大基石等内容。 3、
-
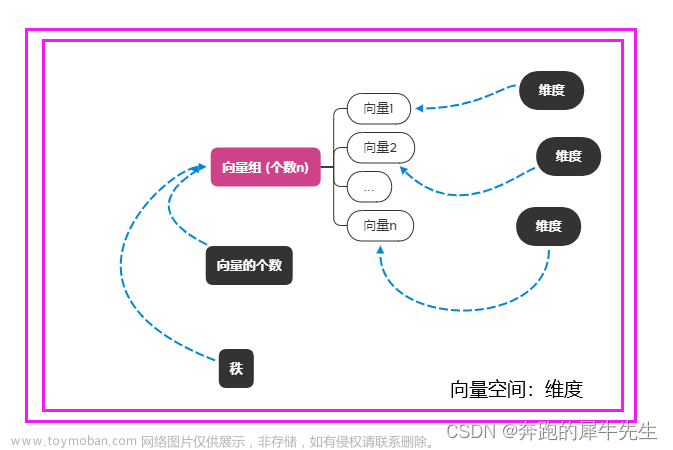
线性代数的学习和整理18:什么是维度,什么是秩?关于秩的各种定理 (未完成)
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
-
19种工程问题,智能优化算法常用指标一键导出为EXCEL,最优值,平均值,标准差,最差值,中位数,秩和检验,箱线图...
常见的智能算法对比方法除了使用经典的CEC函数外, 工程优化问题 也是比较常用的方法。 本期实现在19种工程优化问题上对智能算法的指标进行一键统计! 使你的论文更具说服力! 19种工程优化问题包含如下: 关于上述工程问题的相关介绍,网络上有很多,这里就不再详细
-
MATLAB中对方阵行列式的求解、矩阵的累加和与累乘积进行求解、矩阵的排序、矩阵的秩和迹、以及矩阵的特征值和特征向量的求解
目录 1、方阵的行列式计算 2、累加和与累乘积 (1)累加和 (2)累乘积 3、对于数据进行排序 4、求矩阵的秩 5、矩阵的迹 6、计算矩阵的特征值和特征向量 在线性代数中,对于一个方阵进行求值运算需要先将其转换为行列式,MATLAB中提供过了det函数用于对于方阵的行列式进
-
synchronized 到底锁的是谁?
synchronized 到底锁的是谁? 修饰方法: 1、静态方法 2、非静态方法,锁住的是方法的调用者 修饰代码块 锁住实例 流程: 1、线程A先拿到synModel对象然后给这个 synModel对象加上锁–接着等3s执行输出结束 2、线程B等1s后运行,此时 synModel对象 已经被 A拿到,所以他只能等待 等
-
为什么mysql使用的是B+树而nosql类型的数据库大多数使用的是LSM树
MySQL和LSM Tree(一种基于日志的存储引擎)都是关系型数据库,但它们在数据结构的选择上有所不同。 MySQL使用B+树作为其默认的索引结构,因为B+树在某些方面比LSM树更适合作为默认的索引结构。B+树的查询和更新速度相对较快,而且它的写入操作通常是基于内存的。这意味着
-
认沽期权讲的是什么意思?
多朋友刚接触50ETF期权的交易,虽然和股票交易相似,但50ETF期权的交易界面、下单界面和交易要素比股票交易略微复杂。大家在看空大盘买跌的过程中会遇到“认沽合约”“认沽期权”。那么什么是50ETF认沽期权?认沽期权讲的是什么意思? 本文来自:期权酱 一、 什么是认
-
奖励函数是平稳的是什么意思
在强化学习中,\\\"奖励函数是平稳的\\\"通常指的是奖励信号(reward signal)在不同时间步骤或状态下是稳定的,即其统计性质在整个学习过程中不发生明显的变化。这是一种有关奖励函数的性质,有助于学习算法更好地理解和适应环境。 举一个示例: 考虑一个强化学习代理在训
-
已解决import显示的是灰色
已解决import显示的是灰色 粉丝群里面的一个小伙伴遇到问题跑来私信我,想用import显示的是灰色,但是发生了报错(当时他心里瞬间凉了一大截,跑来找我求助,然后顺利帮助他解决了,顺便记录一下希望可以帮助到更多遇到这个bug不会解决的小伙伴),报错代码如下所示:
-
“不幸的是,你知道的太多了”
《平凡的世界》里有一段话是这么说的:“谁让你读了这么多书,又知道了双水村以外还有个大世界。 如果从小你就在这个天地里日出而作,日落而息,那你现在就会和众乡亲抱同一理想,经过几年的辛劳,像大哥一样娶个满意的媳妇,生个胖儿子,加上你的体魄,会成为一
-
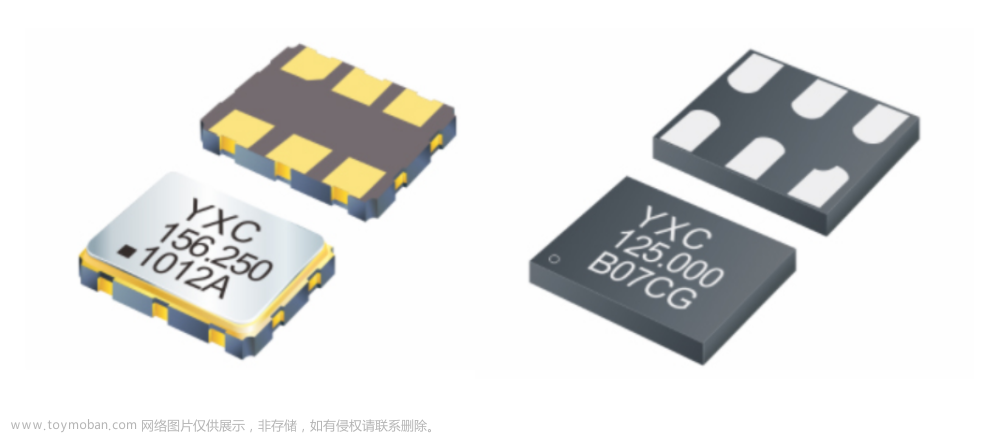
晶振输出的是什么波形?三种类型
有源晶振也叫晶体振荡器,Oscillator;无源晶振有时也叫无源晶体,Crystal,晶体谐振器。 目前差分晶振输出波形主要分为正弦波、方波、准正弦波三类。常用的差分晶振输出均属于方波,输出功率比较大,驱动能力较强,但谐波成分多。 两种输出模式是差分晶振的输出逻
-
【Web】websocket应用的是哪个协议
🍎 个人博客: 个人主页 🏆 个人专栏: Web ⛳️ 功不唐捐,玉汝于成 在当今互联网时代,实时性和即时通讯成为网络应用日益重要的一部分。WebSocket 协议作为一种创新性的通信协议,极大地改善了传统 HTTP 请求-响应模式的限制,为实现高效的双向通信提供了强有力的支